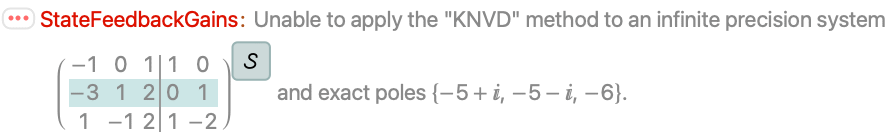StateFeedbackGains[sspec,{p1,…,pn}]
给出系统规范 sspec 的状态反馈增益,以将其闭环极点置于 pi.
StateFeedbackGains[…,"prop"]
给出属性值 "prop".




StateFeedbackGains
StateFeedbackGains[sspec,{p1,…,pn}]
给出系统规范 sspec 的状态反馈增益,以将其闭环极点置于 pi.
StateFeedbackGains[…,"prop"]
给出属性值 "prop".
更多信息和选项




- StateFeedbackGains 也称为极点放置增益或特征值放置.
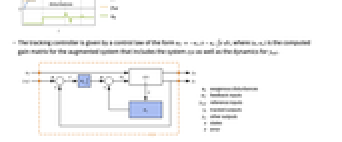
- StateFeedbackGains 用于计算调节控制器或跟踪控制器.
- StateFeedbackGains 通过将闭环系统极点修改为位于 pi 位置起作用.
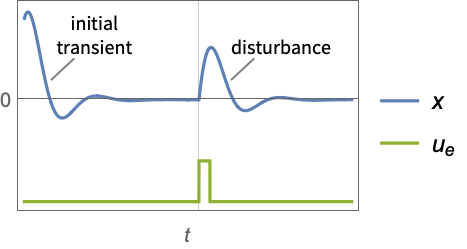
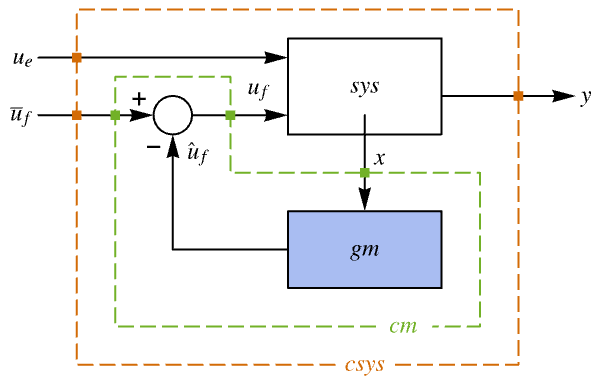
- 调节控制器旨在在尽管有扰动
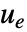 将其推开的情况下将系统保持在平衡状态. 典型范例包括将倒立摆保持在直立位置或保持飞机水平飞行.
将其推开的情况下将系统保持在平衡状态. 典型范例包括将倒立摆保持在直立位置或保持飞机水平飞行. - 调节控制器由
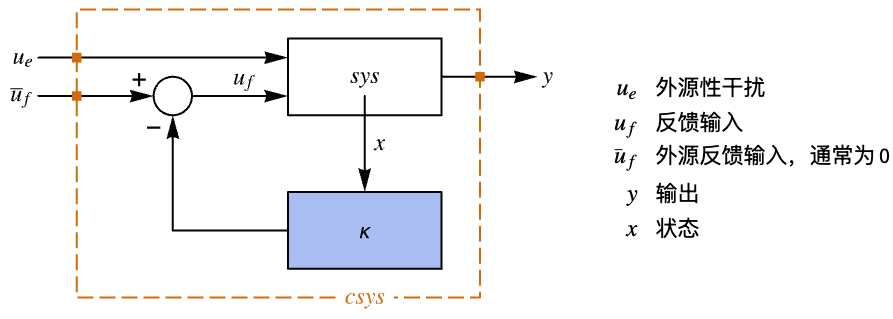
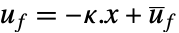 形式的控制律给出,其中
形式的控制律给出,其中 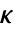 是计算得到的增益矩阵.
是计算得到的增益矩阵. - 要放置的极点数 n 由系统 sys 的 SystemsModelOrder 给出.
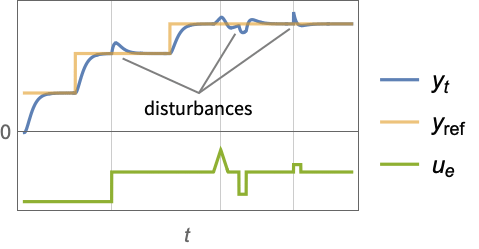
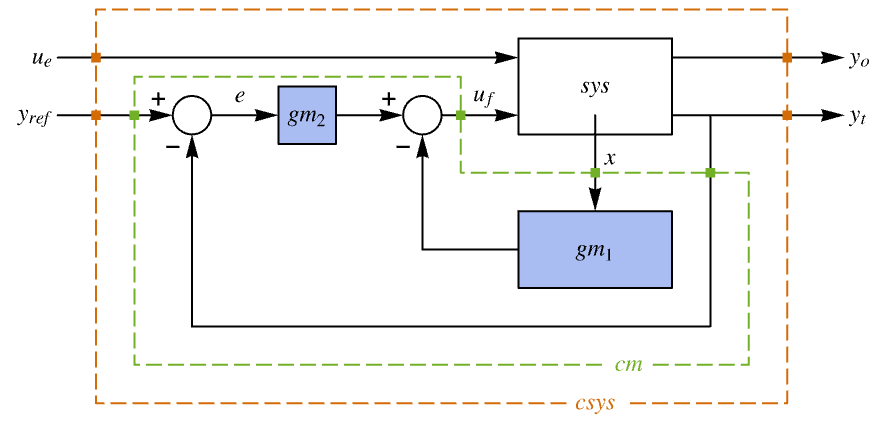
- 跟踪控制器旨在尽管有扰动
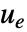 干扰的情况下跟踪参考信号. 典型范例包括汽车的巡航控制系统或机器人的路径跟踪.
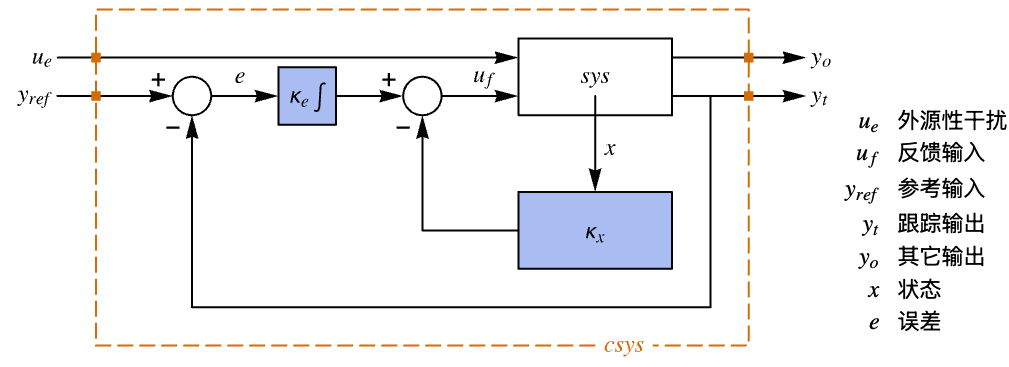
干扰的情况下跟踪参考信号. 典型范例包括汽车的巡航控制系统或机器人的路径跟踪. - 跟踪控制器由形式为
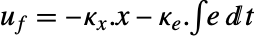 的控制律给出,其中
的控制律给出,其中 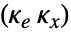 是为增强系统计算的增益矩阵,包括系统 sys 以及
是为增强系统计算的增益矩阵,包括系统 sys 以及 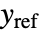 .
. - 要放置的极点数 n 由
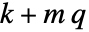 给出,其中
给出,其中 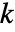 由 sys 的 SystemsModelOrder 给出,
由 sys 的 SystemsModelOrder 给出,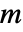 是 yref 的阶数,
是 yref 的阶数,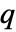 是 yref 的信号数.
是 yref 的信号数. - 极点放置适用于 StateSpaceModel 指定的线性系统:
-
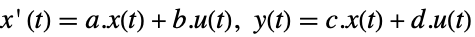
连续时间系统 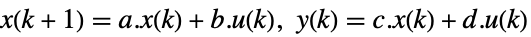
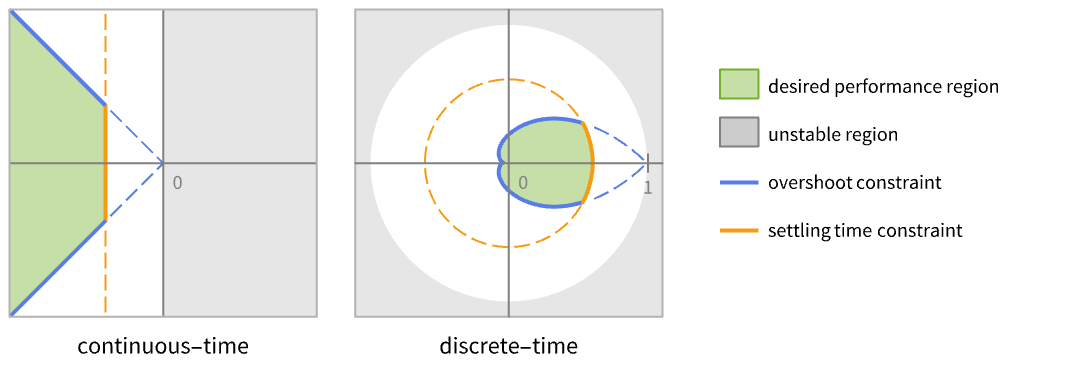
离散时间系统 - 所得闭环系统 csys 的性能主要取决于极点 pi 的位置.
- 通常存在诸如稳定时间之类的性能限制和诸如过冲之类的质量限制. 这些对应于理想的极点位置的某些区域.
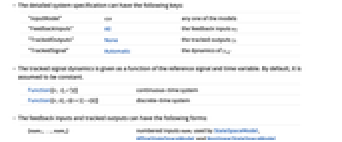
- 系统规范 sspec 是系统 sys 以及 uf、yt 和 yref 规范.
- 系统规范 sspec 可以有以下形式:
-
StateSpaceModel[…] 线性控制输入和线性状态 AffineStateSpaceModel[…] 线性控制输入和非线性状态 NonlinearStateSpaceModel[…] 非线性控制输入和非线性状态 SystemModel[…] 一般系统模型 <|…|> 以 Association 形式给出的详细系统规范 - 详细的系统规范可以有以下密钥:
-
"InputModel" sys 任一模型 "FeedbackInputs" All 反馈输入 uf "TrackedOutputs" None 跟踪输出 yt "TrackedSignal" Automatic yref 的动态 - 跟踪信号动态作为参考信号和时间变量的函数给出. 默认情况下,假定其为常数.
-
Function[{r, t},r'[t]] 连续时间系统 Function[{r,k},r[k+1]-r[k]] 离散时间系统 - 反馈输入和跟踪输出可以有以下形式:
-
{num1,…,numn} StateSpaceModel、AffineStateSpaceModel 和 NonlinearStateSpaceModel 使用的有编号输入 numi {name1,…,namen} SystemModel 使用的有名称输入 namei All 使用所有输入 - 对于诸如 AffineStateSpaceModel、NonlinearStateSpaceModel 和 SystemModel,等非线性系统,系统将围绕其存储的工作点进行线性化.
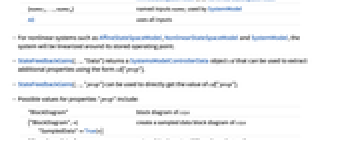
- StateFeedbackGains[…,"Data"] 返回一个 SystemsModelControllerData 对象 cd,该对象可用于使用 cd["prop"] 形式提取其他属性.
- StateFeedbackGains[…,"prop"] 可用于直接获取 cd["prop"] 的值.
- 属性 "prop" 的可能值包括:
-
"BlockDiagram" csys 的框图 {"BlockDiagram",<|"SampledData"True|>} 创建 csys 的采样数据框图 "ClosedLoopPoles" 经线性化 "ClosedLoopSystem" 的极点 "ClosedLoopSystem" 系统 csys {"ClosedLoopSystem", cspec} 对闭环系统形式的详细控制 "ControllerModel" 模型 cm "Design" 控制器设计类型 "DesignModel" 用于设计的模型 "FeedbackGains" 增益矩阵 κ 或其等价物 "FeedbackGainsModel" 模型 gm 或 {gm1,gm2} "FeedbackInputs" 用于反馈的 sys 的输入 uf "InputModel" 输入模型 sys "InputCount" sys 的输入 u 的数量 "OpenLoopPoles" "DesignModel" 的极点 "OutputCount" 系统的输出 y 的数量 "SamplingPeriod" sys 的采样周期 "StateCount" sys 的状态数量 x "TrackedOutputs" 被追踪的 sys 的输出 yt - cspec 的可能密钥包括:
-
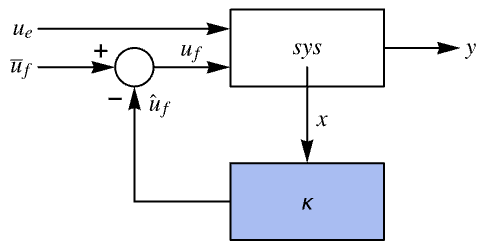
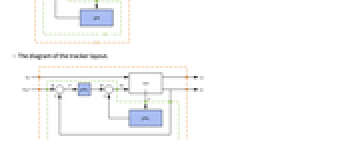
"InputModel" csys 中的输入模型 "Merge" 是否合并 csys "ModelName" csys 的名称Null "SamplingPeriod" 创建采样数据 csys - 稳压器布局图.
- 跟踪器布局图.
- StateFeedbackGains 接受 Method 选项,其中设置由下面任何一个给出:
-
Automatic 自动选择方法 "Ackermann" Ackermann 方法 "KNVD" Kautsky–Nichols–Van Dooren 方法
范例
打开所有单元 关闭所有单元基本范例 (3)
范围 (34)
工厂模型 (6)
连续时间 StateSpaceModel:
离散时间 StateSpaceModel:
描述符 StateSpaceModel:
没有运行点的 AffineStateSpaceModel 被视作 0:
没有运行点的 NonlinearStateSpaceModel 被视作 0:
属性 (12)
StateFeedbackGains 默认返回反馈增益:
跟踪 (5)
选项 (6)
Method (6)
"Ackermann" 方法默认用于具有精确值或符号值的系统:
LinearSolve 用于输入至少与状态一样多的不精确系统:
对于多输入系统,"Ackermann" 方法仅使用一个输入:
应用 (14)
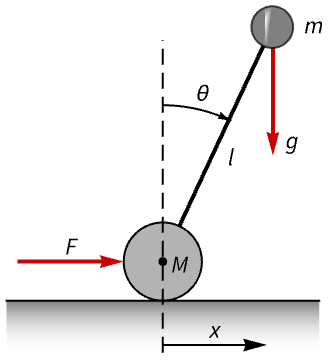
机械系统 (4)
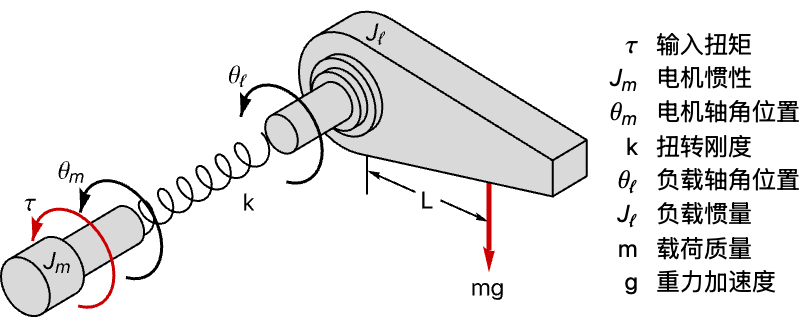
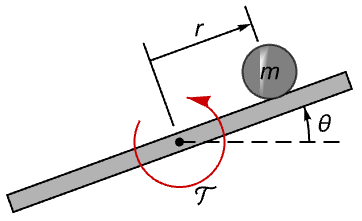
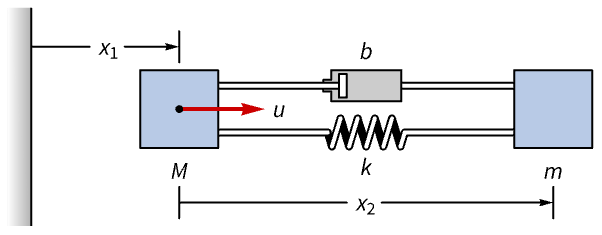
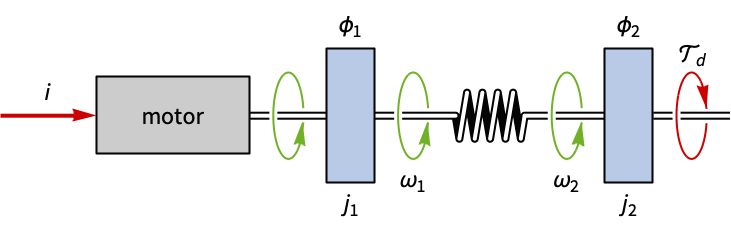
机电系统 (1)
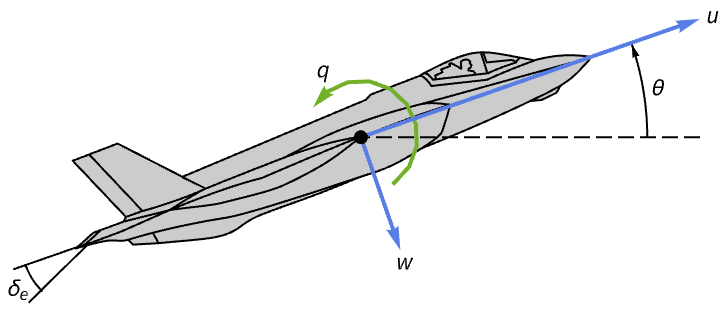
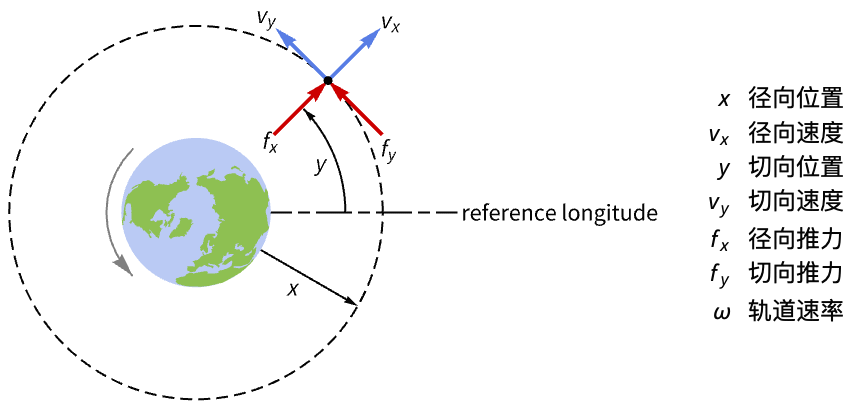
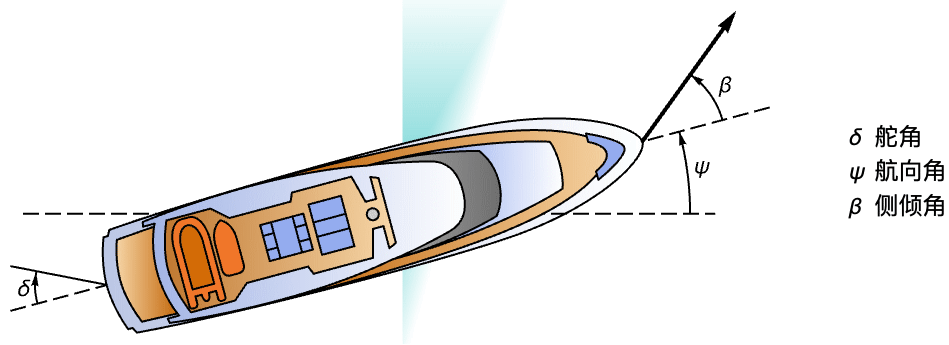
航空航天系统 (2)
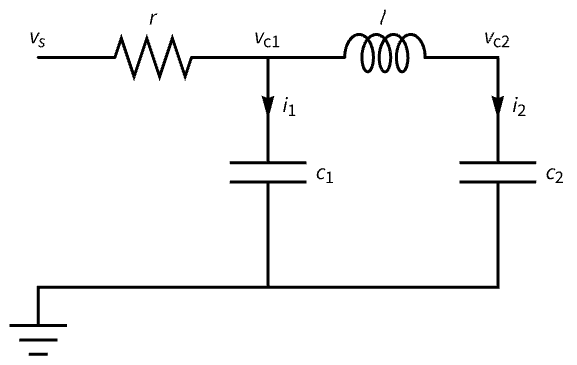
电气系统 (3)
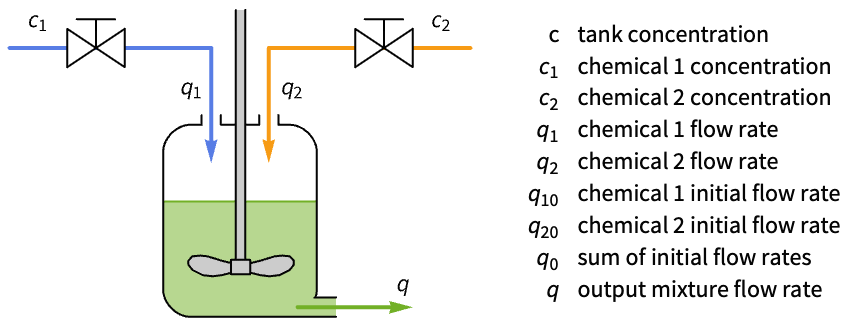
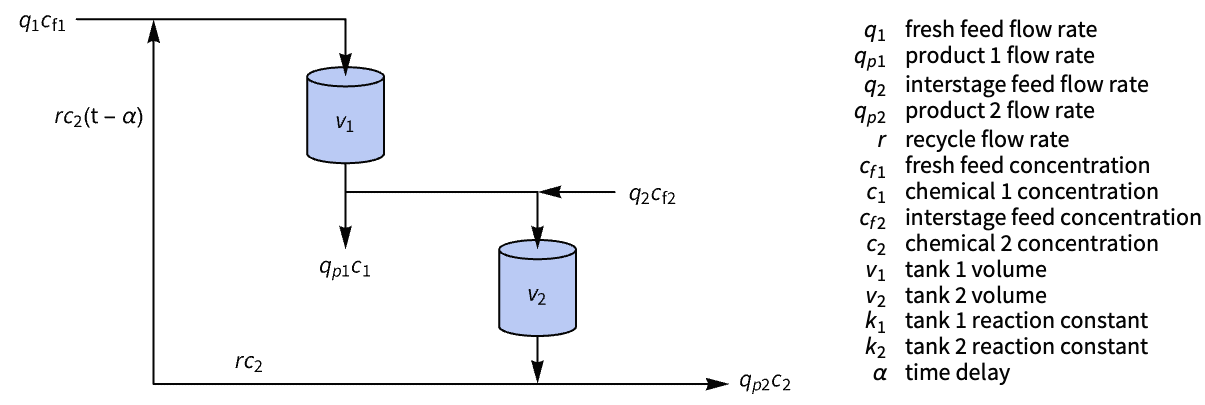
化学系统 (2)
属性和关系 (17)
可控标准 StateSpaceModel 的所有极点都可以使用状态反馈来控制:
可控的非奇异描述符 StateSpaceModel 的所有极点也可以被控制:
只能控制不可控的标准 StateSpaceModel 的子系统:
慢子系统的极点移动到所需位置,快子系统对应的 ![]() 处的极点不变:
处的极点不变:
LQRegulatorGains 和 StateFeedbackGains 对单输入系统产生相同的结果:
StateFeedbackGains 与 LQRegulatorGains 设计的闭环极点:
LQRegulatorGains 给出相同增益:
可以使用对称根轨迹图获得最小化 ![]() ρ c.c x(t)2+u(t)2t 的闭环极点:
ρ c.c x(t)2+u(t)2t 的闭环极点:
使用 LQRegulatorGains 会获得相同增益:
对于 StateSpaceModel 而言,StateFeedbackGains 和 FullInformationOutputRegulator 给出相同结果:

对于这种实现,状态反馈增益的形式为 {{κ,0,…,0}}:
对于这种实现,状态反馈增益的形式为 {{κ,0,…,0}}:
开环和闭环系统都阻塞输入 Sin[2t]:
文本
Wolfram Research (2010),StateFeedbackGains,Wolfram 语言函数,https://reference.wolfram.com/language/ref/StateFeedbackGains.html (更新于 2021 年).
CMS
Wolfram 语言. 2010. "StateFeedbackGains." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2021. https://reference.wolfram.com/language/ref/StateFeedbackGains.html.
APA
Wolfram 语言. (2010). StateFeedbackGains. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/StateFeedbackGains.html 年
BibTeX
@misc{reference.wolfram_2025_statefeedbackgains, author="Wolfram Research", title="{StateFeedbackGains}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/StateFeedbackGains.html}", note=[Accessed: 06-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_statefeedbackgains, organization={Wolfram Research}, title={StateFeedbackGains}, year={2021}, url={https://reference.wolfram.com/language/ref/StateFeedbackGains.html}, note=[Accessed: 06-February-2026]}