StateSpaceModel
StateSpaceModel[{a,b,c,d}]
状態行列 a,入力行列 b,出力行列 c,伝送行列 d の標準状態空間モデルを表す.
StateSpaceModel[{a,b,c,d,e}]
ディスクリプタ行列 e のディスクリプタ状態空間モデルを表す.
StateSpaceModel[sys]
系のモデル sys に対応する状態空間モデルを与える.
StateSpaceModel[eqns,{{x1,x10},…},{{u1,u10},…},{g1,…},τ]
出力 gi,独立変数 τ の微分方程式あるいは差分方程式 eqns の点(xi0,ui0)についてテイラーの線形化を行うことによって得られた状態空間モデルを与える.
詳細とオプション


- StateSpaceModelは,LTI(linear time-invariant,線形時間不変)系としても知られている.
- StateSpaceModelは,通常,コントローラ設計のための系の線形化されたモデルとして使われる.
- 状態
 ,制御入力
,制御入力 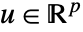 ,出力
,出力 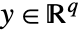 である方程式系
である方程式系  でモデル化された連続時間系はStateSpaceModel[{a,b,c,d}]として指定できる.
でモデル化された連続時間系はStateSpaceModel[{a,b,c,d}]として指定できる. - 状態
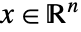 ,制御入力
,制御入力  ,出力
,出力 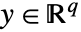 ,サンプリング周期 τ である方程式系
,サンプリング周期 τ である方程式系 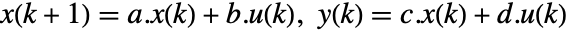 でモデル化された離散時間系はStateSpaceModel[{a,b,c,d},SamplingPeriod->τ]として指定できる.
でモデル化された離散時間系はStateSpaceModel[{a,b,c,d},SamplingPeriod->τ]として指定できる. - ディスクリプタ系は次で指定することができる.
-
StateSpaceModel[{a,b,c,d,e}] 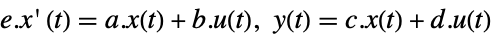
StateSpaceModel[{a,b,c,d,e},SamplingPeriod->τ] 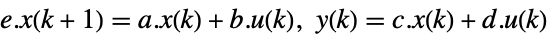
- 遅延時間系は任意の行列でSystemsModelDelayを使って表すことができる.
- n 個の状態,p 個の入力および q 個の出力の系に関しては,行列 a, b, c, d, e の次元が{n,n}, {n,p}, {q,n}, {q,p}, {n,n}になる.
- 次の短縮入力を使うことができる.
-
StateSpaceModel[{a,b,c}] 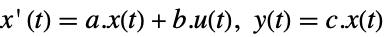
StateSpaceModel[{a,b}] 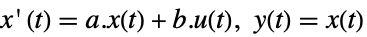
StateSpaceModel[{a,b,c,Automatic,e}] 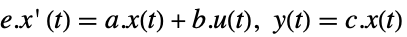
StateSpaceModel[{a,b,Automatic,Automatic,e}] 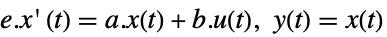
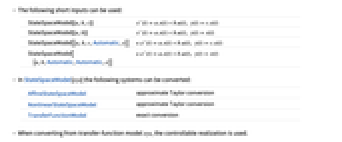
- StateSpaceModel[sys]では,次の系を変換することができる.
-
AffineStateSpaceModel 近似テイラー(Taylor)変換 NonlinearStateSpaceModel 近似テイラー変換 TransferFunctionModel 厳密変換 - 伝達関数モデル sys から変換する場合は,可制御実現が使われる.
- 方程式の入力については,デフォルトの線形化点 xi0および uj0がゼロであるとみなされる.
- 使用可能なオプション
-
DescriptorStateSpace Automatic 標準実現あるいは記述子実現 ExternalTypeSignature Automatic 埋め込まれたコードの変数型 SamplingPeriod Automatic サンプリング周期 StateSpaceRealization Automatic 正準実現 SystemsModelLabels Automatic 入力,出力,状態変数のラベル
例題
すべて開くすべて閉じる例 (4)
スコープ (41)
基本的な用法 (12)
この変数は,AffineStateSpaceModel表現では可視である:
記述子モデル (6)
デフォルトで,記述子行列 e は恒等行列であると仮定される:
Automaticを使ってすべての状態を出力として持つ記述子系を作成する:
あらゆるケースの記述子モデルを標準モデルに変換することはできないかもしれない:
時間遅延モデル (3)
SystemsModelDelayを使って遅延がある系をモデル化する:
モデル変換 (13)
ランダム過程 (6)
MAProcessの状態空間表現:
オプション (15)
アプリケーション (27)
力学系 (11)
ニュートンの第2法則を使用して,質量・バネ・ダンパ系の状態空間モデルを計算する:

これは線形系で,近似なしで線形状態空間形式に入れることができる:
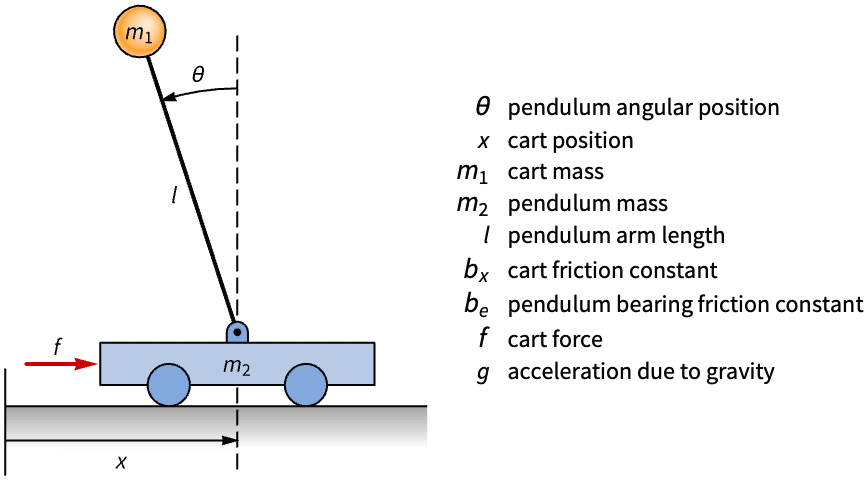
振動吸収材の状態空間モデルをラグランジュとレイリー(Rayleigh)散逸関数を使って計算する:
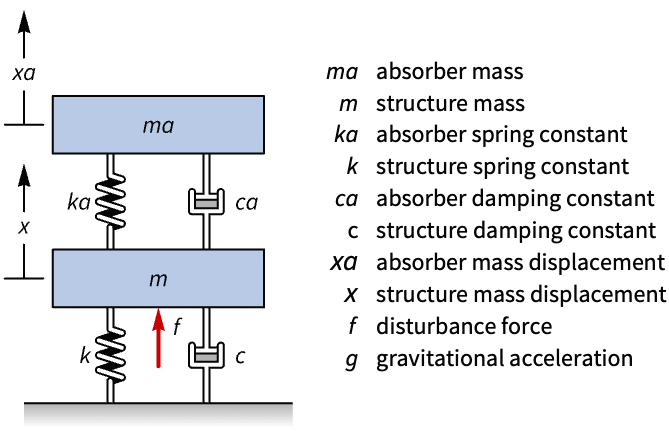
可撓軸に負荷がかかったモーターで構成されるマルチドメインの系の状態空間モデルを計算する:
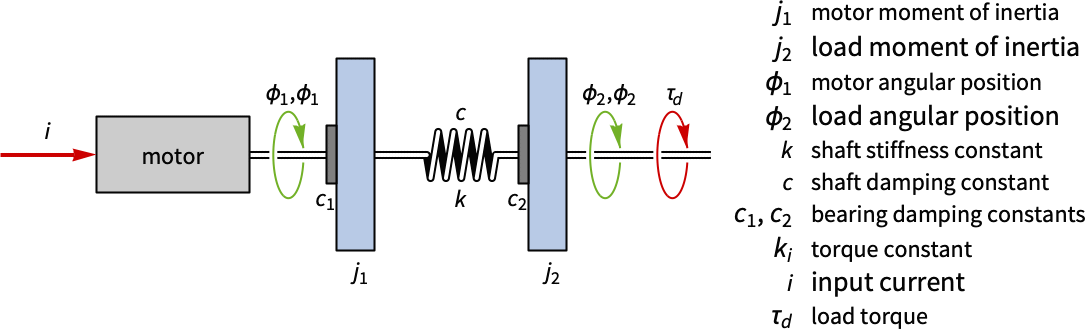
ボールとビームの系の近似離散時間状態空間モデルを,連続時間方程式から始めて計算する:
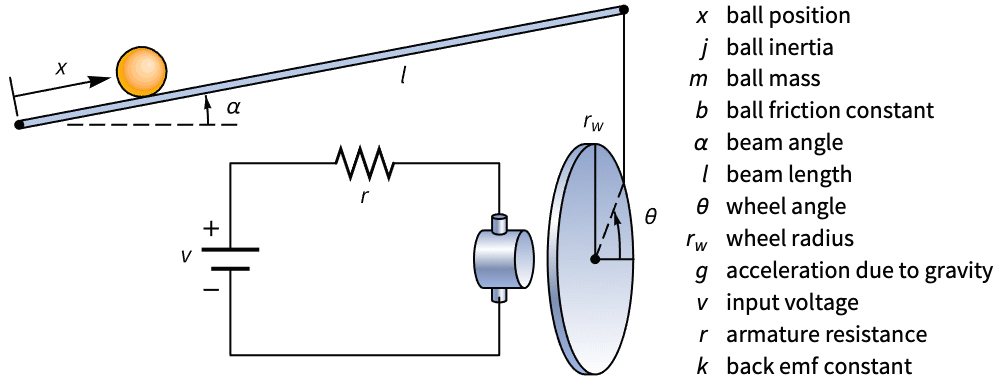
傾いたモーターについてのキルヒッホフ(Kirchhoff)の電圧方程式.電機子インダクタンスないものと仮定する:
水平であることを維持しながらビームを動かしたことによるボールの移動位 ![]() :
:
どちらのモデルでも,ボールは水平ビーム上でバランスが取れている:
さまざまな平衡位置に関する振子の状態空間モデルを計算し,それらを比較する:
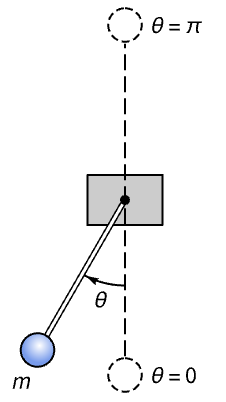
パラメータ値の集合についての2つの平衡位置の付近の状態空間モデル:
0付近で線形化されたモデルの応答は安定しているのに対し,180°付近のそれは不安定である:
これは,2つの平衡点が安定した固有値と不安定な固有値を持つためである:
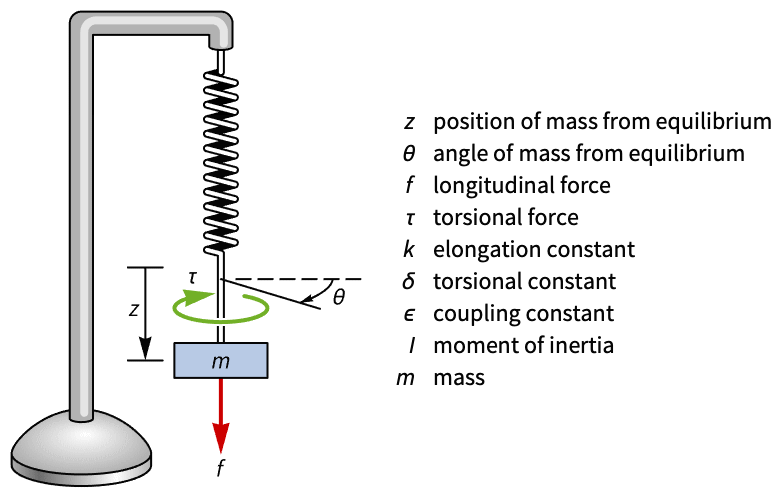
結合動力学を持つWilberforce振子の状態空間モデルを計算し,振り子に対するさまざまな入力の有効性を比較する:
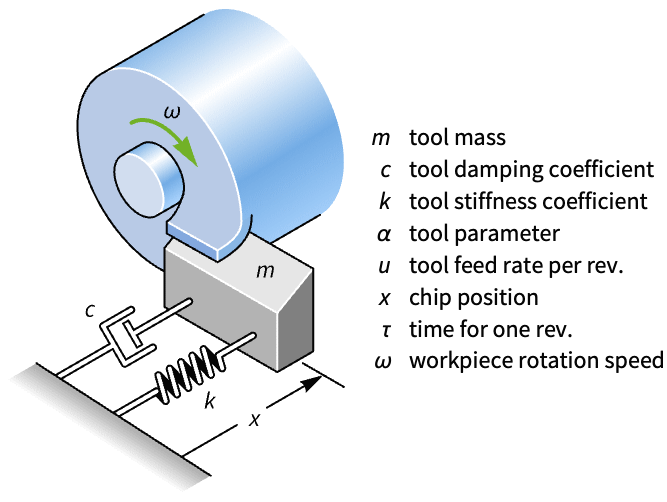
旋盤の切削加工の状態空間モデルを計算する.モデルの遅延は系チャタリング動作を捉えるために必要である:
状態空間モデルでは,極配置等の状態フィードバック制御手法が可能になる. 倒立振子の極を ![]() 平面の左側に配置して,振子のバランスを取る:»
平面の左側に配置して,振子のバランスを取る:»
一連の閉ループ極を使用して振子のバランスを取るコントローラ:
状態空間モデルは,費用関数を最小化する最適状態フィードバックゲインの計算の基本である.最適制御を使って可撓軸の振動を減衰する:»
状態空間モデルは追跡問題を解くためにも使われる.ボールとビームの位置を追跡するコントローラを設計する:»
航空宇宙系 (6)
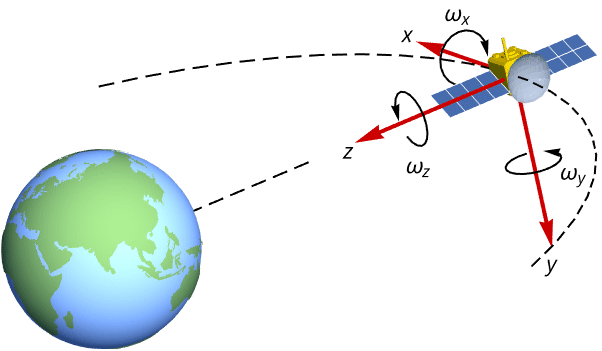
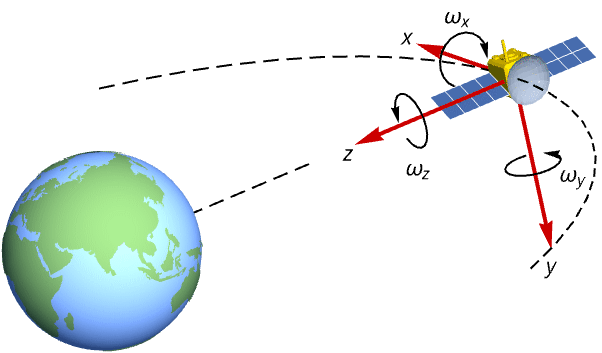
状態空間モデルは航空宇宙系のモデリングにとって有益である.オイラーの運動方程式から始まる衛星の姿勢力学の状態空間モデルを構築する:
状態空間モデルはモデル解析において使用される.ハリアー・ジャンプ・ジェット(Harrier VTOL jet)の状態空間モデルを構築してその可制御性を評価する:
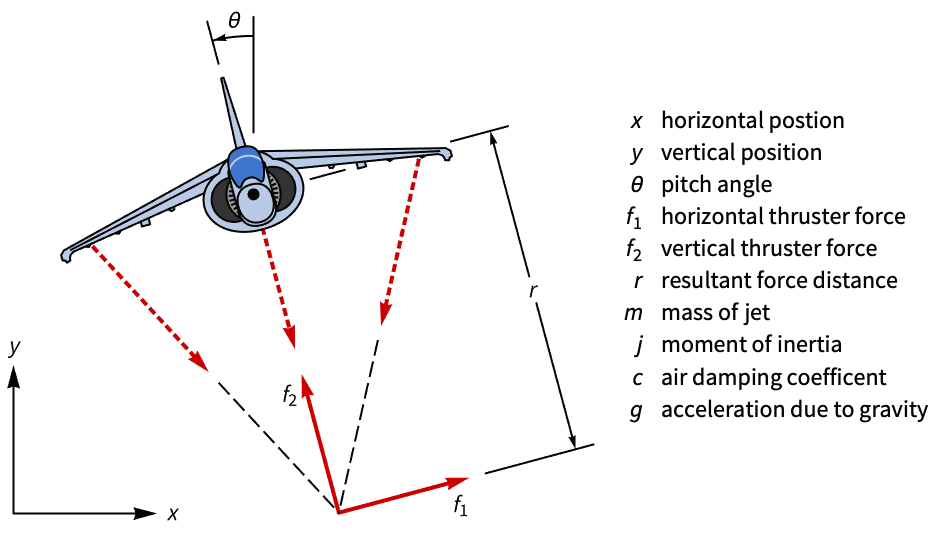
航空機が完全に制御可能となるためにはどちらの入力も必要である:
状態空間モデルは指定の出力に複数の入力が影響を与えるMIMO系の分析に有益である. 状態空間モデル表現を使って状態フィードバック制御を使用するボーイング747のヨー力学における補助翼と方向舵の有効性を比較する:
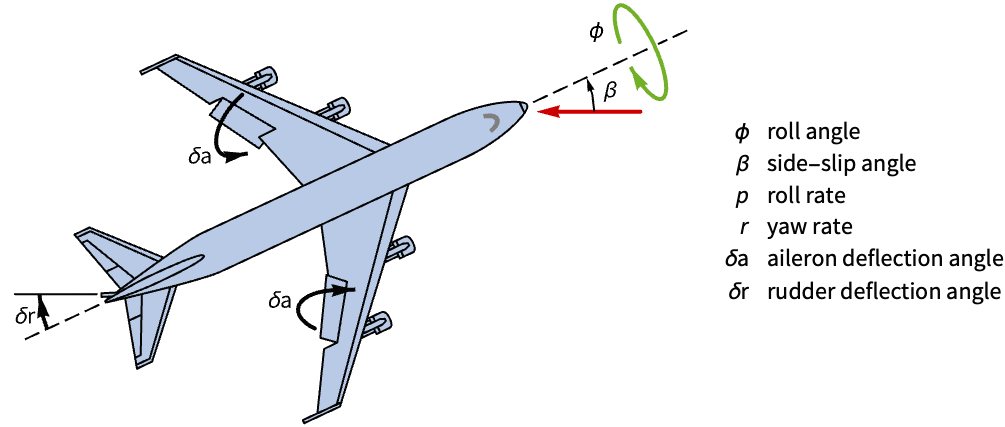
状態,入力,出力の各行列からの,航空機の横移動の状態空間モデル:
かじを含む状態空間モデルと唯一の入力としてエルロンを含む状態空間モデルを入手する:
状態空間モデルは離散時間状態フィードバックコントローラの設計に役に立つ.ボーイング747の縦方向のダイナミクスの状態空間モデルを入手し,離散時間状態フィードバック制御を使ってその操作品質を向上させる:

近似された離散時間費用関数を最小化する最適コントローラを計算する:
離散時間コントローラもまた連続時間モデルを近似することで設計できる.連続時間状態空間モデルを近似することでHarrier VTOLジェットを安定化させる離散時間コントローラを設計する:»
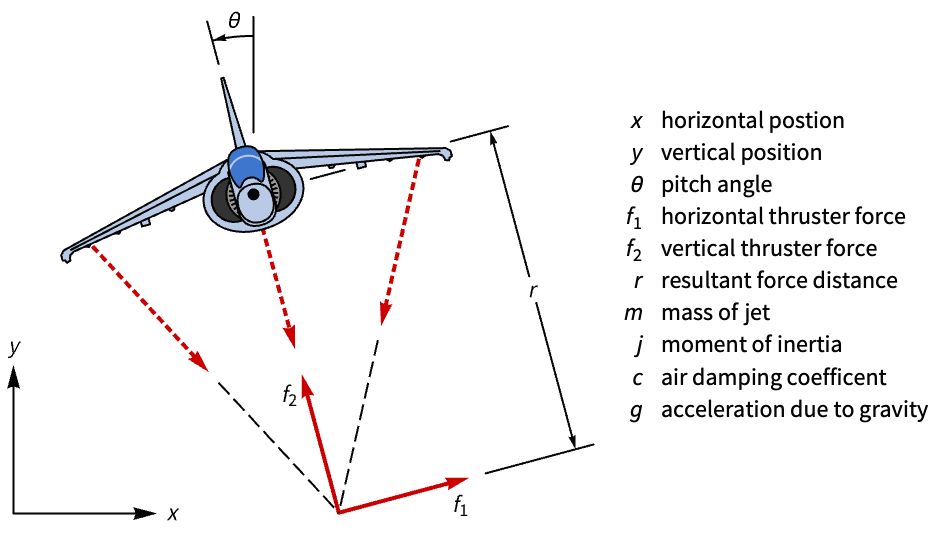
コントローラがないと,ジェット機の水平位置はピッチに外乱が加わると制御されない:
ジェット機を安定させるための離散時間状態フィードバックコントローラを設計する:
ジェット機はコントローラによって初期外乱に対して安定化される:
状態空間モデルは推定器調整などの出力フィードバックコントローラーの設計にも使用できる.離散時間モデルを使用して,衛星が天底を指す方向を維持するために必要な角速度を追跡する推定調整器を設計する:
生物系 (2)
化学系 (3)
状態空間モデルは,化学反応過程のモデリングに役に立つ.発酵過程の状態空間モデルを構築し,希釈率の指数関数的減衰に対する応答のシミュレーションを行う:
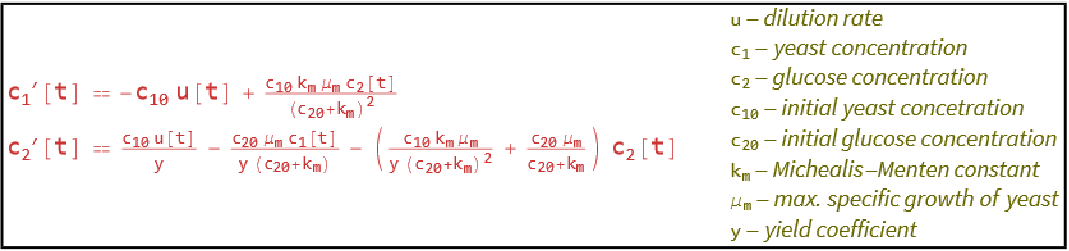
希釈率 ![]() における指数関数的減衰によって発酵過程は停止することになる:
における指数関数的減衰によって発酵過程は停止することになる:
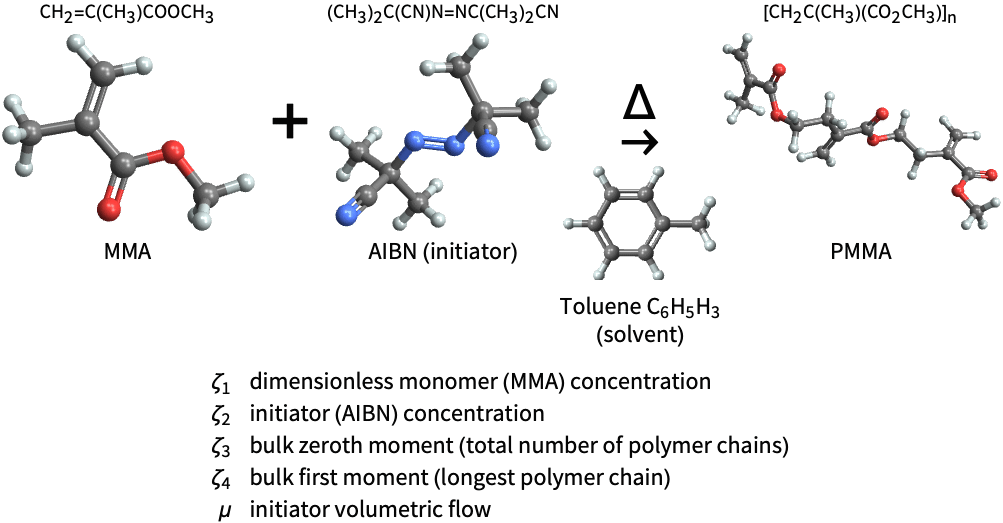
状態空間モデルは,連続撹拌槽反応器(CSTR)の化学動力学のモデル化にとって理想的である.メタクリル酸メチル (MMA)の重合のための状態空間モデルを構築する:
その極は ![]() 平面の左側にあり,モデルが安定していることを示している:
平面の左側にあり,モデルが安定していることを示している:
MMAの濃度が低下すると,開始剤の体積流量が増加し,PMMA の合成が示される:
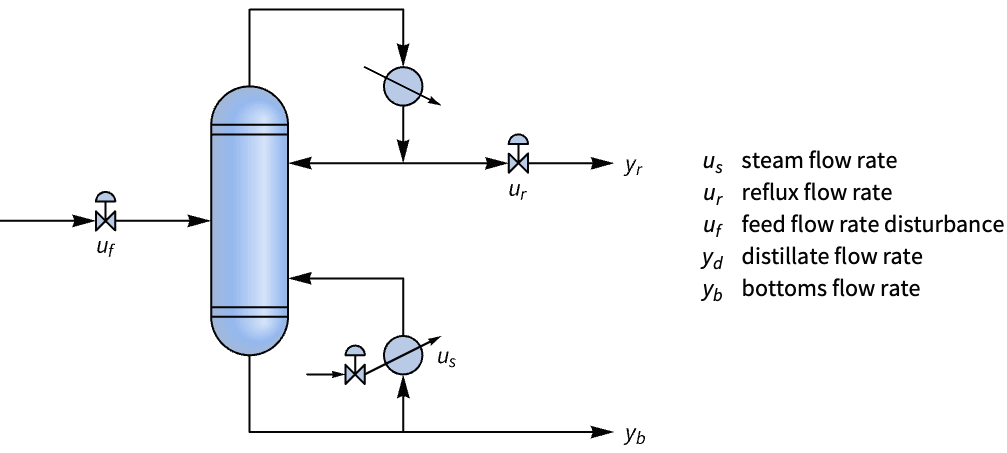
状態空間モデルは,遅延がある系のモデル化に役に立つ.Wood–Berry伝達関数モデルから蒸留塔の状態空間モデルを取得し,その応答を同じモデルの遅延なし近似と比較する:
電気系 (4)
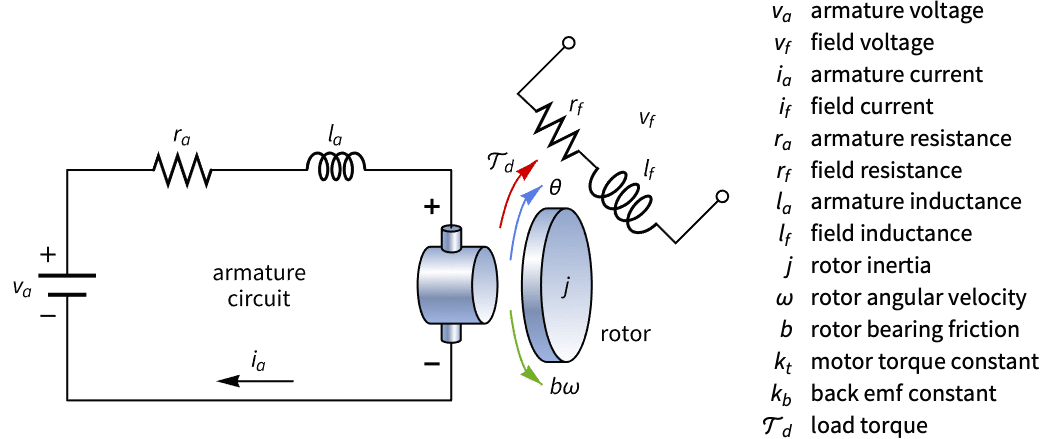
電機子電圧と場の電圧を入力してその制御性を分析するDCモーターの状態空間モデルを構築する:

記号状態空間モデルを使ってパラメータがあるモデルのシミュレーションができる. 演算増幅機(オペアンプ)回路の記号状態空間モデルをその支配方程式から構築し,さまざまなパラメータ値におけるその出力位相と振幅を解析する:
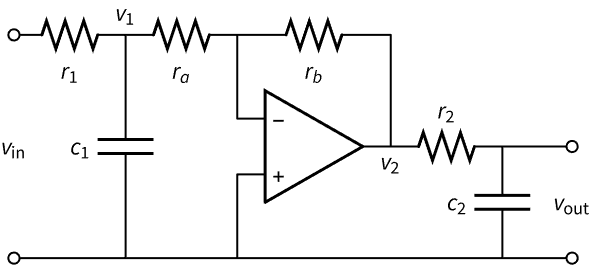
キルヒッホフ(Kirchhoff)の電流法則(KCL)を使った支配方程式:
状態空間モデルは,微分方程式と代数方程式が混合した系を表すことができる.RLC回路の記述子状態空間モデルをその微分方程式から,標準的な状態空間モデルをその微分方程式から構築する:
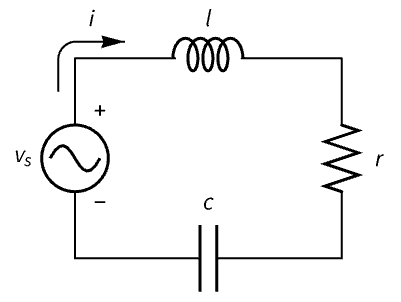
記述子状態空間モデルはキルヒッホフの方程式が代数的であるために取得できる:
純粋な微分方程式を使うと標準的な状態空間モデルが入手できる:
状態空間モデルは追跡問題を解決するために使用される.変化するトルク負荷とセンサーノイズが存在するDCモーターの推定器ベースの追跡コントローラを設計する:»
特性と関係 (20)
相似変換によって関連付けられた状態空間モデルの伝達関数モデルは等しい:
これは,Cayley-Hamilton定理に従って,それ自身の固有多項式を満足する:
したがって,状態行列の固有値が負であるなら,応答は指数関数的に減衰して0になる:
固有値が複素数で左平面にあるなら,応答は振動して![]() に減衰する:
に減衰する:
固有値ペアが虚軸上にあって残りが負の場合,応答には減衰されていない振動が含まれる:
これは,その固有値が負の値と虚軸上のペアを含んでいるからである:
固有値の一つが0で残りが負の場合,応答は非零のオフセットを含む:
離散時間モデルの固有値が単位円内にあるなら,その応答は0に減衰する:
テキスト
Wolfram Research (2010), StateSpaceModel, Wolfram言語関数, https://reference.wolfram.com/language/ref/StateSpaceModel.html (2014年に更新).
CMS
Wolfram Language. 2010. "StateSpaceModel." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/StateSpaceModel.html.
APA
Wolfram Language. (2010). StateSpaceModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StateSpaceModel.html