SystemModelMeasurements
SystemModelMeasurements[sspec]
computes measurement properties for the system specification sspec.
SystemModelMeasurements[sspec,prop]
computes the property prop.
SystemModelMeasurements[sim,…]
computes properties for the SystemModelSimulationData object sim.
Details and Options




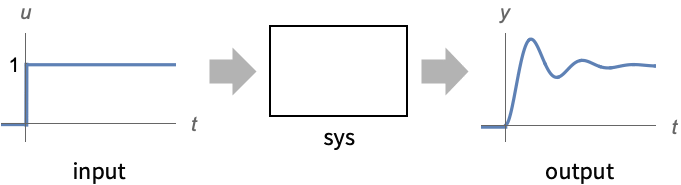
- SystemModelMeasurements is typically used to quantify system performance and quality by measuring how it responds to a step input.
- The measurements only make sense for stable systems, i.e. systems for which bounded inputs result in bounded outputs.
- The system sys can have the following forms:
-
StateSpaceModel[…] state-space model TransferFunctionModel[…] transfer function model AffineStateSpaceModel[…] affine state-space model NonlinearStateSpaceModel[…] non-linear state-space model DiscreteInputOutputModel[…] discrete input-output model SystemModel[…] general system model <…> detailed system specification sspec given as an Association - The system specification sspec can have the following keys:
-
"Model" sys any one of the models with inputs "SimulationInterval" Automatic simulation interval {tinit,tfinal} "Inputs" All inputs to turn on {u1,…} "Outputs" Automatic variables to measure {y1,…} - For a system with multiple inputs, measurements are performed with each input turned on one at a time.
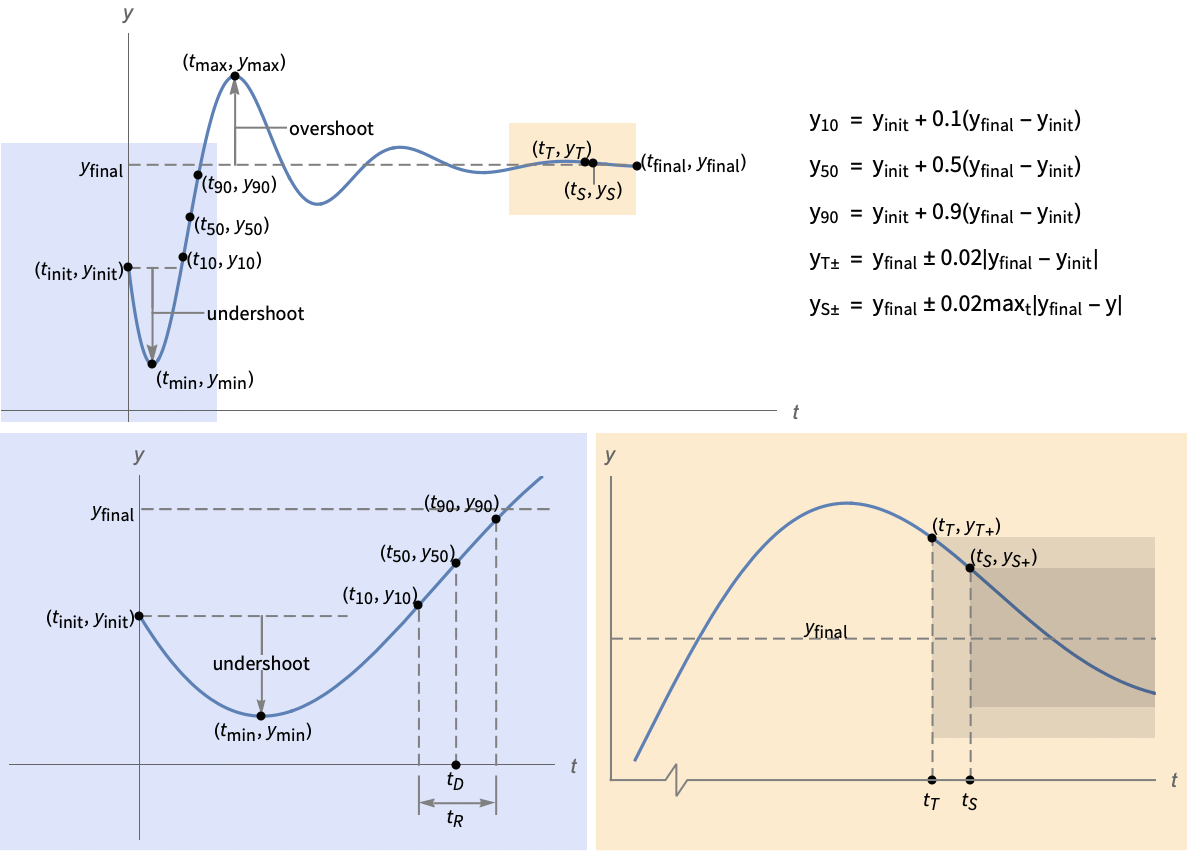
- Measurement properties typically depend on the initial value, yinit, and final value, yfinal, of the measured output y.
- Time properties prop include:
-
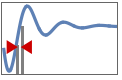
"RiseTime" time 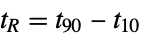 for output to change from 10% to 90% of the final value
for output to change from 10% to 90% of the final value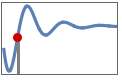
"DelayTime" time 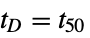 for output to reach 50% of the final value
for output to reach 50% of the final value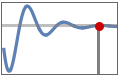
"TransientTime" time  for output transients to subside, i.e.
for output transients to subside, i.e. ![TemplateBox[{{{y, (, t, )}, -, {y, _, {(, final, )}}}}, Abs]/max_t TemplateBox[{{{y, (, t, )}, -, {y, _, {(, final, )}}}}, Abs]<=0.02 TemplateBox[{{{y, (, t, )}, -, {y, _, {(, final, )}}}}, Abs]/max_t TemplateBox[{{{y, (, t, )}, -, {y, _, {(, final, )}}}}, Abs]<=0.02](Files/SystemModelMeasurements.en/9.png) for
for 
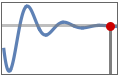
"SettlingTime" time 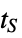 for output to settle, i.e.
for output to settle, i.e. 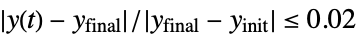 for
for 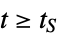
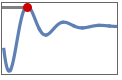
"MinValueTime" time tmin for output to reach the minimum ymin, i.e. 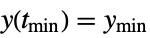
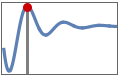
"MaxValueTime" time tmax for output to reach the maximum ymax, i.e. 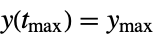
- Value properties prop include:
-
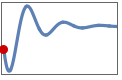
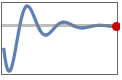
"InitialValue" initial value yinit, i.e. 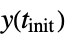
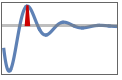
"FinalValue" final value yfinal, i.e. 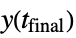
"MaxOvershootPercent" maximum percent of signal excess beyond yfinal, i.e. 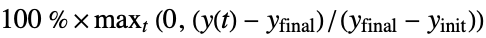
"MaxUndershootPercent" maximum percent of signal excess beyond yinit, i.e. 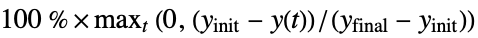
"MinValue" minimum value 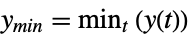
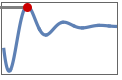
"MaxValue" maximum value 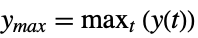
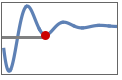
"SettlingMinValue" - minimum value
ysmin once the output has risen, i.e.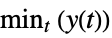 for
for 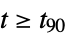
"SettlingMaxValue" - minimum value
ysmax once the output has risen, i.e.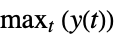 for
for 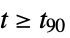
- Response properties prop include:
-
InterpolatingFunction[…] "Response" response signal 
"Plot" response plot - The following options can be given:
-
Method Automatic measurement method ProgressReporting $ProgressReporting control display of progress TargetUnits None units in measurement properties - Method settings take the form Method{"sub1"val1,…}.
- Method suboptions "subi" include:
-
"RiseTimeLowerThreshold" 0.1 fraction of signal change at start of rise time "RiseTimeUpperThreshold" 0.9 fraction of signal change at end of rise time "DelayTimeThreshold" 0.5 - fraction of signal change at end of delay time
"SettlingTimeThreshold" 0.02 settling time threshold - The option TargetUnits controls the units of quantities in measurement properties:
-
None no unit (default) "Unit" unit defined in model "DisplayUnit" display unit defined in model unit explicit unit {unitt,unit} units for time and data
Examples
open allclose allBasic Examples (3)
Scope (13)
Basic Uses (4)
Compute measurements for a SystemModel:
Compute measurements for an AffineStateSpaceModel:
Compute measurements for a discrete multiple-input multiple-output StateSpaceModel:
Compute measurements for SystemModelSimulationData:
Properties (5)
Options (7)
Method (3)
ProgressReporting (1)
Control progress reporting with ProgressReporting:
Applications (7)
Basic Applications (4)
Study how the settling time varies with the location of poles for a discrete-time system:
Compute the closed-loop system for several different designs based on pole locations:
Compute the setting times for the resulting systems:
Show the pole location and the corresponding settling time:
Or look at the actual step responses:
Study how overshoot varies with the location of poles for a discrete-time system:
Compute the closed-loop system for several different designs based on pole locations:
Compute the maximum overshoot for the resulting systems:
Show the pole location and the corresponding maximum overshoot:
Or look at the actual step responses:
Study how the settling time varies with the location of poles for a continuous-time system:
Compute the closed-loop system for several different designs based on pole locations:
Compute the setting times for the resulting systems:
Show the pole location and the corresponding settling time:
Or look at the actual step responses:
Study how the overshoot varies with the location of poles for a continuous-time system:
Compute the closed-loop system for several different designs based on pole locations:
Compute the maximum overshoot for the resulting systems:
Show the pole location and the corresponding maximum overshoot:
Ball and Beam (1)
Camera Stabilizer (1)
Start with a model of a camera attached to the top of a moving vehicle:
Simulate the model with a vertical force perturbation:
Compute the extremes for the position of the camera and plot the full response:
Linearize the model around the equilibrium point:
Generate a closed-loop system for the controlled model:
Simulate the closed-loop system with the same perturbation:
Quadcopter Drone (1)
Start with a model of a quadcopter drone:
Design a controller that tracks the altitude of the drone:
Introduce an observer with EstimatorRegulator and produce the closed-loop system:
When a unit step input is provided as reference, the drone elevates in a few seconds to the desired height:
Properties & Relations (2)
The "Response" measurement property is computed with SystemModelSimulate:
Simulate with UnitStep as input and extract the response:
The "Plot" measurement property is computed with SystemModelPlot:
SystemModelPlot has multiple options to customize plots as desired:
Text
Wolfram Research (2022), SystemModelMeasurements, Wolfram Language function, https://reference.wolfram.com/language/ref/SystemModelMeasurements.html.
CMS
Wolfram Language. 2022. "SystemModelMeasurements." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SystemModelMeasurements.html.
APA
Wolfram Language. (2022). SystemModelMeasurements. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SystemModelMeasurements.html