SystemModelMeasurements

SystemModelMeasurements[sspec]

computes measurement properties for the system specification sspec.

SystemModelMeasurements[sspec,prop]

computes the property prop.

SystemModelMeasurements[sim,…]

computes properties for the SystemModelSimulationData object sim.

Details and Options

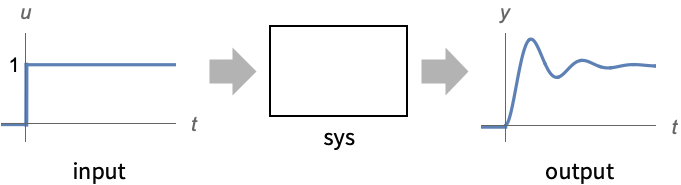
  • SystemModelMeasurements is typically used to quantify system performance and quality by measuring how it responds to a step input.
  • The measurements only make sense for stable systems, i.e. systems for which bounded inputs result in bounded outputs.
  • The system sys can have the following forms:
  • StateSpaceModel[…]state-space model
    TransferFunctionModel[…]transfer function model
    AffineStateSpaceModel[…]affine state-space model
    NonlinearStateSpaceModel[…]non-linear state-space model
    DiscreteInputOutputModel[…]discrete input-output model
    SystemModel[…]general system model
    <|…|>detailed system specification sspec given as an Association
  • The system specification sspec can have the following keys:
  • "Model"sysany one of the models with inputs
    "SimulationInterval"Automaticsimulation interval {tinit,tfinal}
    "Inputs"Allinputs to turn on {u1,…}
    "Outputs"Automaticvariables to measure {y1,…}
  • For a system with multiple inputs, measurements are performed with each input turned on one at a time.
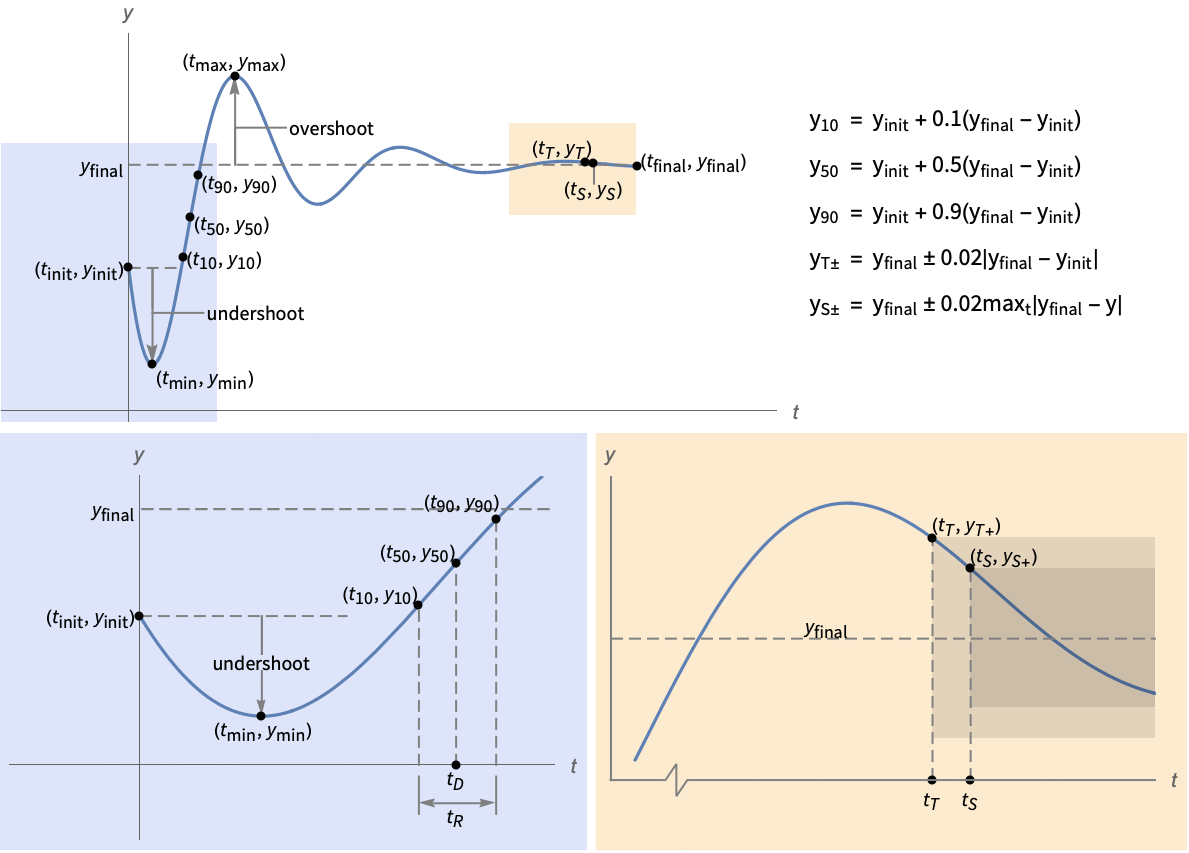
  • Measurement properties typically depend on the initial value, yinit, and final value, yfinal, of the measured output y.
  • Time properties prop include:
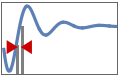
  • "RiseTime"time for output to change from 10% to 90% of the final value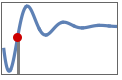
    "DelayTime"time 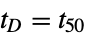for output to reach 50% of the final value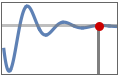
    "TransientTime"time 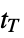for output transients to subside, i.e. TemplateBox[{{{y, (, t, )}, -, {y, _, {(, final, )}}}}, Abs]/max_t TemplateBox[{{{y, (, t, )}, -, {y, _, {(, final, )}}}}, Abs]<=0.02 for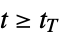
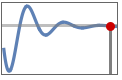
    "SettlingTime"time 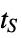for output to settle, i.e. 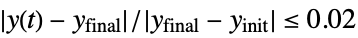for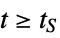
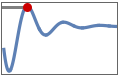
    "MinValueTime"time tmin for output to reach the minimum ymin, i.e.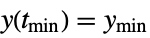
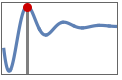
    "MaxValueTime"time tmax for output to reach the maximum ymax, i.e.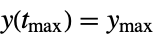
  • Value properties prop include:
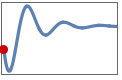
  • "InitialValue"initial value yinit, i.e.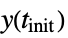
    "FinalValue"final value yfinal, i.e.
    "MaxOvershootPercent"maximum percent of signal excess beyond yfinal, i.e.
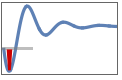
    "MaxUndershootPercent"maximum percent of signal excess beyond yinit, i.e.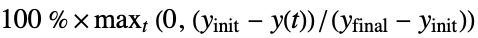
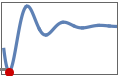
    "MinValue"minimum value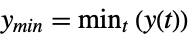
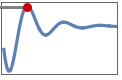
    "MaxValue"maximum value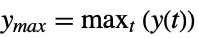
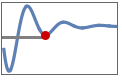
    "SettlingMinValue"
  • minimum value
    • ysmin once the output has risen, i.e.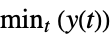 for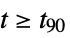
    "SettlingMaxValue"
  • minimum value
    • ysmax once the output has risen, i.e.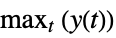 for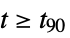
  • Response properties prop include:
  • InterpolatingFunction[…]"Response"response signal
    "Plot"response plot
  • The following options can be given:
  • Method Automaticmeasurement method
    ProgressReporting $ProgressReportingcontrol display of progress
    TargetUnits Noneunits in measurement properties
  • Method settings take the form Method{"sub1"val1,…}.
  • Method suboptions "subi" include:
  • "RiseTimeLowerThreshold"0.1fraction of signal change at start of rise time
    "RiseTimeUpperThreshold"0.9fraction of signal change at end of rise time
    "DelayTimeThreshold"0.5
  • fraction of signal change at end of delay time
    • "SettlingTimeThreshold"0.02settling time threshold
  • The option TargetUnits controls the units of quantities in measurement properties:
  • Noneno unit (default)
    "Unit"unit defined in model
    "DisplayUnit"display unit defined in model
    unitexplicit unit
    {unitt,unit}units for time and data

Examples

open allclose all

Basic Examples  (3)

Compute measurement properties for a model:

Compute the settling time for a single-output model:

Compute measurement properties for simulation data:

Compute the rise time for the simulated variable:

Scope  (13)

Basic Uses  (4)

Compute measurements for a SystemModel:

Compute measurements for an AffineStateSpaceModel:

Compute measurements for a discrete multiple-input multiple-output StateSpaceModel:

Compute measurements for SystemModelSimulationData:

Properties  (5)

Compute the maximum overshoot for a single-output model:

Compute the settling time for a model:

Compute the maximum and minimum values for a model:

Compute the response for a single-output model:

Plot the response for a single-output model:

System Specification  (4)

Specify a custom simulation interval:

Specify a custom set of inputs to turn on:

Specify a custom set of variables to measure:

Specify both a custom set of inputs to turn on and a custom set of variables to measure:

Options  (7)

Method  (3)

Set custom rise time thresholds:

Set a custom settling time threshold:

Set a custom delay time threshold:

ProgressReporting  (1)

Control progress reporting with ProgressReporting:

TargetUnits  (3)

Compute measurements with the output units defined in the model:

Compute measurements with the time and output units defined in the model:

Compute measurements with custom time and output units:

Applications  (7)

Basic Applications  (4)

Study how the settling time varies with the location of poles for a discrete-time system:

Compute the closed-loop system for several different designs based on pole locations:

Compute the setting times for the resulting systems:

Show the pole location and the corresponding settling time:

Or look at the actual step responses:

Study how overshoot varies with the location of poles for a discrete-time system:

Compute the closed-loop system for several different designs based on pole locations:

Compute the maximum overshoot for the resulting systems:

Show the pole location and the corresponding maximum overshoot:

Or look at the actual step responses:

Study how the settling time varies with the location of poles for a continuous-time system:

Compute the closed-loop system for several different designs based on pole locations:

Compute the setting times for the resulting systems:

Show the pole location and the corresponding settling time:

Or look at the actual step responses:

Study how the overshoot varies with the location of poles for a continuous-time system:

Compute the closed-loop system for several different designs based on pole locations:

Compute the maximum overshoot for the resulting systems:

Show the pole location and the corresponding maximum overshoot:

Or look at the actual step responses:

Ball and Beam  (1)

Study a controlled system of a ball placed at the top of a beam:

When passing an input torque, the controller responds by moving the ball to a position off-center that cancels it:

With all torques cancelled, the angle of the beam goes back to 0:

Compute the time it takes the system to settle:

Camera Stabilizer  (1)

Start with a model of a camera attached to the top of a moving vehicle:

Simulate the model with a vertical force perturbation:

Compute the extremes for the position of the camera and plot the full response:

Linearize the model around the equilibrium point:

Design a controller:

Generate a closed-loop system for the controlled model:

Simulate the closed-loop system with the same perturbation:

The camera oscillations are now 10 times smaller:

The magnitude of the control effort is within reason:

Quadcopter Drone  (1)

Start with a model of a quadcopter drone:

Design a controller that tracks the altitude of the drone:

Introduce an observer with EstimatorRegulator and produce the closed-loop system:

When a unit step input is provided as reference, the drone elevates in a few seconds to the desired height:

Properties & Relations  (2)

The "Response" measurement property is computed with SystemModelSimulate:

Simulate with UnitStep as input and extract the response:

The "Plot" measurement property is computed with SystemModelPlot:

SystemModelPlot has multiple options to customize plots as desired:

Wolfram Research (2022), SystemModelMeasurements, Wolfram Language function, https://reference.wolfram.com/language/ref/SystemModelMeasurements.html.

Text

Wolfram Research (2022), SystemModelMeasurements, Wolfram Language function, https://reference.wolfram.com/language/ref/SystemModelMeasurements.html.

CMS

Wolfram Language. 2022. "SystemModelMeasurements." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SystemModelMeasurements.html.

APA

Wolfram Language. (2022). SystemModelMeasurements. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SystemModelMeasurements.html

BibTeX

@misc{reference.wolfram_2023_systemmodelmeasurements, author="Wolfram Research", title="{SystemModelMeasurements}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/SystemModelMeasurements.html}", note=[Accessed: 20-April-2024 ]}

BibLaTeX

@online{reference.wolfram_2023_systemmodelmeasurements, organization={Wolfram Research}, title={SystemModelMeasurements}, year={2022}, url={https://reference.wolfram.com/language/ref/SystemModelMeasurements.html}, note=[Accessed: 20-April-2024 ]}