TimeValue[s,i,t]
i で指定された利息に対する時間 t における担保 s の時間価値を計算する.


TimeValue
TimeValue[s,i,t]
i で指定された利息に対する時間 t における担保 s の時間価値を計算する.
詳細とオプション


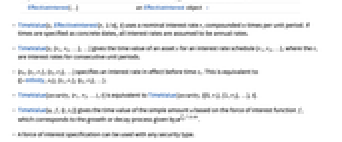
- TimeValue[a, i, t]は,単純な額 a と正の時間の値 t について,実行利息を i とした場合の時間 t における a の将来価値すなわち累積価値を与える. »
- TimeValue[a, i, t]は,単純な額 a と負の時間の値 t について,実行利息を i とした場合の a の現在価値または割引価値を与える. »
- TimeValueは任意の数式または記号式に使うことができる.TimeValueが返す記号式は,SolveやFindRootのような組込み関数を使って,利率,支払い,または期間について解くことができる.
- 担保 s は,以下の追加的な形式んおよび解釈を持つことができる.
-
Annuity 期間の終りにおける一連の支払い » AnnuityDue 期間の初めにおける一連の支払い Cashflow キャッシュフローの流れ » - TimeValue[Annuity[…],interest,t]は,年金の時間価値を t 時点での単一の同等の支払いとして計算する.年金の計算には,住宅ローンの評価,債券の価格設定,支払いまたは利回りの計算などがある.
- TimeValue[Cashflow[…],interest,t]は,キャッシュフローの時間価値を t 時点の単一の同等の支払いとして計算する.可能なキャッシュフロー計算には,正味現在価値,割引キャッシュフロー,内部収益率などがある.
- TimeValue[s,i,{t,t1}]は,利息 i を使用して,時刻 t1から t までの累積または割引された時間価値を計算する.時刻 t1はキャッシュフローの発生の基準点として機能する. »
- TimeValue[s,i]はTimeValue[s,i,0]に等しい.
- TimeValue[…,t]はTimeValue[…,{t,0}]に等しい.
- TimeValue[s,i,t]では,利息 i は次の形式で指定することができる.
-
r 実行利率 {r1,r2,…} 単位時間区間に適用される利率一覧表 » {{t1,r1},{t2,r2},…} 指定時間に変化する利率一覧表 » {p1->r1,p2->r2,…} 実行利率の期間構造 » function 時間の関数として与えられる利力 » EffectiveInterest[…] EffectiveInterestオブジェクト » - TimeValue[s,EffectiveInterest[r,1/n],t]は単位時間ごとに n 回複利計算を行った名目利率 r を使う.時間が具体的な日付で指定されている場合は,すべての利率が年率であると推定される.
- TimeValue[s,{r1,r2,…},…]は利率予定{r1,r2,…}での資産 s の時間価値を与える.ただし,riは連続する単位時間の利率である.
- {r0,{t1,r1},{t2,r2},…}は時間 t1以前に有効な利率を指定する.これは{{-Infinity,r0},{t1,r1},{t2,r2},…}に等しい.
- TimeValue[security,{r1,r2,…},t]はTimeValue[security,{{0,r1},{1,r2},…},t]に等しい.
- TimeValue[a,f,{t,t1}]は式
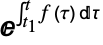 で与えられる成長あるいは減衰過程に対応する利力関数 f に基づいた単純額 a の時間価値を与える.
で与えられる成長あるいは減衰過程に対応する利力関数 f に基づいた単純額 a の時間価値を与える. - 利力指定は任意の担保のタイプに使うことができる.
- 使用可能なオプション
-
Assumptions $Assumptions パラメータに関する仮定 GenerateConditions False パラメータについての条件を生成するかどうか
例題
すべて開く すべて閉じる例 (4)
スコープ (20)
5%の名目金利を用い,四半期複利で1000ドルの将来価値を求める:
指定した時点で有効となる利率のスケジュールを用いた現在価値:
6%の金利で$1000を$3000に増やすために必要な期間数:
連続支払いフローのある年金額は利力指定と組み合せることができる:
2010年1月1日に1,000ドルを投資し,7.5%で運用した場合の3年後の将来価値:
単位時間区間ごとの利率のスケジュールを用いた5期間後の将来価値:
利率はTimeSeriesとして与えることができる:
オプション (2)
アプリケーション (15)
3年後に$1000とするために年利9%で投資しなければならない額を求める:
利率8%で四半期複利計算を行った場合の5年後の$5000の累積価値を求める:
利率6%の半年複利計算で$1000が$1500になるまでに必要な時間を求める:
利力が![]() (t は時間)の場合の n 年後の1の将来価値を求める:
(t は時間)の場合の n 年後の1の将来価値を求める:
最初の5年間の実行利率が r1,次の5年間の実行利率が r2,最後の5年間の実行利率が r3の場合に15年後の$1000の累積価値を計算する式を求める:
$1000 を年利8%の四半期複利で投資した場合に,資産を10年で使い切るために各四半期末にいくら引き出せばよいかを計算する:
5年間四半期ごとに$1000支払った場合の現行価値が$16000となる四半期複利の利率を求める:
最初の6年間の実行利率が5%で次の4年間が4%の場合の1年$100 の年金額の10年間の累積額を求める:
将来キャッシュフローの収入を生む初期投資額$1000の正味現在価値を求める:
8年後に$600受け取るために今$100を支払い,5年後に$200,10年後に最後の支払いを行うとする.この投資の収益率が8%で年に2回の複利計算をする場合と等しくなるための最終の支払額を求める:
$100,$200,$500の支払いがそれぞれ2年後,3年後,8年後にある.$800の支払いが利率5%に等しくなる点を求める:
現在価値$2000の2年後の値と現在価値$3000の4年後の値が$4000になる実行利率を求める:
任意の時のローン残高はそれから先の支払の現在額に等しいので,Annuityを使って償還表を作ることができる:
特性と関係 (2)
考えられる問題 (3)
長期あるいは頻度の高い年金あるいは公債の利率を求めるためにはSolveの代りにFindRootが必要にあることもある:
TimeValueが査定期間に達するために一覧表内に十分の利率があるかどうかを判断するためには,査定期間は数値でなければならない:
TimeSeriesで利率を指定するためには,最初の時点が0でなければならない:
インタラクティブな例題 (1)
Manipulateを使って一連のキャッシュフローが変数集合に対して持つさまざまな依存性を調べる:
テキスト
Wolfram Research (2010), TimeValue, Wolfram言語関数, https://reference.wolfram.com/language/ref/TimeValue.html (2024年に更新).
CMS
Wolfram Language. 2010. "TimeValue." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/TimeValue.html.
APA
Wolfram Language. (2010). TimeValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TimeValue.html
BibTeX
@misc{reference.wolfram_2025_timevalue, author="Wolfram Research", title="{TimeValue}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/TimeValue.html}", note=[Accessed: 04-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_timevalue, organization={Wolfram Research}, title={TimeValue}, year={2024}, url={https://reference.wolfram.com/language/ref/TimeValue.html}, note=[Accessed: 04-February-2026]}