FinancialBond[params,ambientparams]
gives the value of a financial bond instrument.
FinancialBond[params,ambientparams,prop]
computes the specified property prop.


FinancialBond
FinancialBond[params,ambientparams]
gives the value of a financial bond instrument.
FinancialBond[params,ambientparams,prop]
computes the specified property prop.
Details and Options





- FinancialBond represents a class of financial instruments involving a series of coupon payments together with a principal payment made at maturity.
- FinancialBond works with numeric or arbitrary symbolic expressions.
- FinancialBond[params,ambientparams,{prop1,prop2,…}] computes multiple properties and returns the results as a list.
- FinancialBond[params,ambientparams,"Rules"] computes all available properties.
- All parameters in FinancialBond are given as a set of rules {param1,val1,param2,val2,…}.
- Possible parameters include:
-
"FaceValue" face value or par value "Coupon" coupon rate or payment function "Maturity" maturity or call/put date "CouponInterval" coupon payment interval "RedemptionValue" redemption value (if different from face value) - Possible ambient parameters include:
-
"InterestRate" yield to maturity or yield rate "Settlement" settlement date "DayCountBasis" day count convention - Settlement and maturity specifications can be entered as dates or abstract time units.
- The coupon may be specified as a single rate or a time-dependent payment function.
- Possible interest specifications include:
-
r single yield rate {r1,r2,…} schedule of spot rates applied over unit time intervals {{t1,r1},{t2,r2},…} schedule of rates changing at the specified time {p1->r1,p2->r2,…} term structure of interest rates function force of interest, given as a function of time - The following settings can be given for "DayCountBasis":
-
"30/360" US bond basis "30E/360" Eurobond basis (ISDA 2006) "30E/360German" Eurobond basis (ISDA 2000, German) "30E+/360" 30E+/360 day count convention "ActualICMA" actual/actual ICMA "ActualISDA" actual/actual ISDA "Actual/365" actual/365 (fixed) "Actual/360" actual/360 (French) "Actual/365L" actual/365L "ActualAFB" actual/actual AFB/FBF master agreement Automatic precise calendrical calculations - FinancialBond can compute the following properties:
-
"Value" price adjusted for accrued interest "FullValue" unadjusted price "AccruedInterest" accrued interest at settlement "Duration" Macaulay duration "ModifiedDuration" modified duration "Convexity" convexity "CouponPeriodDays" days in coupon period containing the settlement "CouponToSettlementDays" days from previous coupon to settlement "SettlementToCouponDays" days from settlement to next coupon "NextCouponDate" next coupon date "PreviousCouponDate" previous coupon date "RemainingCoupons" remaining coupon payments "AccruedFactor" fraction of coupon payment representing the accrued interest - When abstract time units are used in a FinancialBond with maturity
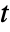 , the specified settlement time
, the specified settlement time 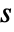 must lie within the range of the bond's existence (
must lie within the range of the bond's existence (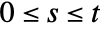 ).
). - By convention, yield to maturity and coupon specifications are assumed to be nominal with a compounding interval equal to the coupon payment interval. By using the EffectiveInterest function or a functional interest rate specification, any desired compounding can be achieved.
- When a coupon interval q is specified, coupon payments occur at times q, 2q, …. Without a coupon interval, payments are assumed to occur at times 1, 2, …. With a setting "CouponInterval"->0, the function specified by "Coupon"->f is taken to be continuous.
- When dates are specified in FinancialBond, and when either the coupon or interest rate is specified as a function, or when the interest rate is specified as a list of rates or a term structure, the function assumes that time 0 occurs at the nearest point before the settlement date that represents an integral number of years from the maturity date.
- Payment functions may be given as recurrence relations. RSolve can be used to convert recurrence relations into functions of time for use in FinancialBond.
- When abstract time units are used in FinancialBond, calendrical properties are not applicable.
- The following options can be given:
-
Assumptions $Assumptions assumptions made about parameters GenerateConditions False whether to generate conditions on parameters
Examples
open all close allBasic Examples (4)
Issue price of a 30-year annual coupon bond of $1000 with a 6% yield:
Price of a 10-year semiannual coupon bond with a 5% yield 9 months after the issue date:
Price of a 4% quarterly coupon bond maturing December 31, 2030, and settling September 5, 2013:
Accrued interest for a semiannual bond maturing on December 31, 2030, and settling on November 12, 2010, using the "Actual/360" day count convention:
Scope (12)
FinancialBond works with symbolic parameters and can find closed-form expressions:
Apart can be used to expose the discount factor coefficients on individual payments:
Apart may need to be applied multiple times to fully decompose the expression:
Symbolic solutions to equations involving FinancialBond can be found:
An integer can be used as a payment interval to specify payments occurring only once every several periods:
FinancialBond can be given a term structure of interest rates or a list of future spot rates:
When dates are given along with a rate structure that varies with time, time 0 is assumed to occur at the nearest point before the settlement date that represents an integral number of years from the maturity date. In this case, time 0 occurs on December 31, 2010:
A bond's payment growth function can be any function:
Value a bond under the discount process specified by a force of interest ![]() :
:
FinancialBond can take a functional (growing) coupon together with a force of interest:
A console bond can be valued using Infinity as the maturity date:
Similarly, an equity stock with a growing dividend can be valued using zero face value:
Calculate the duration of the same stock:
FinancialBond takes a nominal yield and assumes a compounding equal to the coupon frequency. However, it may be desirable to use a different compounding frequency. EffectiveInterest can be used to find a rate that gives the correct effective discounting after being compounded at the coupon frequency:
A constant force of interest can be used to create the same continuous compounding:
Expectation can be used to find the expected value of the price of a $1000 par value bond callable at $1100 at some unknown time between years 10 and 15:
Assume the unknown call date will follow a normal distribution centered at year 12.5:
RSolve can be used to convert recurrence relations into functions of time alone:
The recurrence relation above represents payments growing by a fixed rate, at every payment. Its solution is a function of time alone and is suitable for use in FinancialBond:
Applications (9)
Implied coupon rate of a semiannual bond priced at $980 with a yield of 5%:
A zero coupon bond will pay $1000 at the end of 10 years and is currently selling for $400. Find the implied yield rate compounded semiannually:
Implied yield to maturity for a quarterly coupon bond settling on January 6, 2018, and valued at $900:
Find the price of a 10-year, inflation-adjusted bond with a par value of $1000 and with annual coupons. The initial coupon rate is 7%, and each coupon is 3% greater than the preceding one. The bond's redemption value is $1200:
Find the accrued interest for the bond above, assuming it is purchased three months into its life:
A $100 par value 10-year bond with 8% semiannual coupons is issued on May 1. Slightly over 2 years later on May 15, the bond sells for $88. Find the yield rate on that date assuming exact calendrical computations:
Price of a semiannual callable bond with a redemption value of $1200, a call date on December 31, 2020, and a settlement date of July 12, 2010:
Days until the next coupon date for a 4% quarterly coupon bond maturing December 31, 2030, and settling September 5, 2013, using the "30/360" day count convention:
A 20-year semiannual coupon bond has a nominal rate of 8% and a price of $1722.25. The bond can be called at par on any coupon date starting at the end of year 15. Find the par value that will guarantee at least a 6% yield:
Find the call price that will guarantee at least a 7% yield if this same bond had a par value of 1000 and a price of $1300:
Find the maximum yield an investor can hope to achieve if this bond had a call of 1100 and a price of $900:
Duration and convexity for a semiannual bond maturing on December 31, 2030, and settling on November 12, 2010, using the "Actual/360" day count convention:
Properties & Relations (4)
Plot bond price against the growth rate of its coupon payment:
Duration and convexity can be calculated manually using a symbolic yield and the derivative function D:
Calculate the same quantities using FinancialBond properties:
On a coupon date, the value of a FinancialBond object will give the same value as an Annuity object having the same payment frequency and a final payment equal to the par value of the bond:
EffectiveInterest can be used to determine the actual discount rates that were used by FinancialBond when a term structure is given:
Possible Issues (1)
Although a bond can be defined in terms of an annuity with a final payment, FinancialBond gives a price whereas TimeValue gives a time-valued equivalent for an Annuity. There is no difference when calculating a present value (time = 0), but there are differences when using a time period other than zero:
Neat Examples (2)
Plot a bond's actual sensitivity to the yield against its estimated sensitivity given by the duration:
FinancialBond can be used to illustrate the effects of adjusting for accrued interest:
Related Guides
History
Text
Wolfram Research (2010), FinancialBond, Wolfram Language function, https://reference.wolfram.com/language/ref/FinancialBond.html.
CMS
Wolfram Language. 2010. "FinancialBond." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FinancialBond.html.
APA
Wolfram Language. (2010). FinancialBond. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FinancialBond.html
BibTeX
@misc{reference.wolfram_2025_financialbond, author="Wolfram Research", title="{FinancialBond}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/FinancialBond.html}", note=[Accessed: 14-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_financialbond, organization={Wolfram Research}, title={FinancialBond}, year={2010}, url={https://reference.wolfram.com/language/ref/FinancialBond.html}, note=[Accessed: 14-January-2026]}