TimeValue
TimeValue[s,i,t]
calculates the time value of a security s at time t for an interest specified by i.
Details and Options


- For a simple amount a and an effective interest rate i, TimeValue[a,i,t] gives the future or accumulated value of a at time t.
- TimeValue[a,i,-t] gives the present or discounted value of a simple amount a for an effective interest rate i.
- Times can be given in abstract units or as dates.
- TimeValue works with arbitrary numeric or symbolic expressions. Symbolic formulas returned by TimeValue can be solved for interest rates, payments, or time periods using built-in functions such as Solve and FindRoot.
- In TimeValue[s,…], the security s can be given as a simple amount or as a Cashflow, Annuity, or AnnuityDue object.
- TimeValue[s,i,{t,t1}] computes the time value accumulated or discounted from time t1 to t using interest i. Time t1 serves as a reference point for cash flow occurrences.
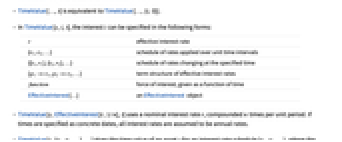
- TimeValue[s,i] is equivalent to TimeValue[s,i,0].
- TimeValue[…,t] is equivalent to TimeValue[…,{t,0}].
- In TimeValue[s,i,t], the interest i can be specified in the following forms:
-
r effective interest rate {r1,r2,…} schedule of rates applied over unit time intervals {{t1,r1},{t2,r2},…} schedule of rates changing at the specified time {p1->r1,p2->r2,…} term structure of effective interest rates function force of interest, given as a function of time EffectiveInterest[…] an EffectiveInterest object - TimeValue[s,EffectiveInterest[r,1/n],t] uses a nominal interest rate r, compounded n times per unit period. If times are specified as concrete dates, all interest rates are assumed to be annual rates.
- TimeValue[s,{r1,r2,…},…] gives the time value of an asset s for an interest rate schedule {r1,r2,…}, where the ri are interest rates for consecutive unit periods.
- {r0,{t1,r1},{t2,r2},…} specifies an interest rate in effect before time t1. This is equivalent to {{-Infinity,r0},{t1,r1},{t2,r2},…}.
- TimeValue[security,{r1,r2,…},t] is equivalent to TimeValue[security,{{0,r1},{1,r2},…},t].
- TimeValue[a,f,{t,t1}] gives the time value of the simple amount a based on the force of interest function f, which corresponds to the growth or decay process given by
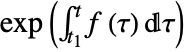 .
. - A force of interest specification can be used with any security type.
- The following options can be given:
-
Assumptions $Assumptions assumptions made about parameters GenerateConditions False whether to generate conditions on parameters
Examples
open allclose allBasic Examples (14)
Future value of $1000 at an effective interest rate of 5% after 3 compounding periods:
Present value of $1000 at 5% over 3 periods:
Future value of $1000 using a nominal rate of 5% with quarterly compounding:
TimeValue works with symbolic parameters:
Present value at 6% of a 12-period annuity with payments of $100:
Future value at 6% of a series of cash flows occurring at regular intervals:
Future value in three years' time of $1000 invested on January 1, 2010, at 7.5%:
Number of periods required to grow $1000 to $3000 at a 6% interest rate:
Future value after 5 periods using a schedule of rates over unit time intervals:
Present value using a schedule of rates effective at the specified times:
Present value of an amount paid at time 10 using a term structure of interest rates:
Future value using a schedule of rates over irregular time intervals:
Compute the future value after three time periods using a force of interest ![]() :
:
Scope (12)
Symbolic time value computations:
Time value computation using a rate schedule:
Time value based on a force of interest function:
A symbolic cash flow computation:
A symbolic annuity calculation:
Symbolic solution for the number of periods:
Solve an annuity calculation for the payment amount:
An annuity with a continuous payment flow can be coupled with a force of interest specification:
Hours, minutes, and seconds can be given in date specifications:
Rates can be given as a TimeSeries:
Options (2)
Applications (15)
Find the amount that must be invested at a rate of 9% per year in order to accumulate $1000 at the end of 3 years:
Find the accumulated value of $5000 over 5 years at 8% compounded quarterly:
Find how much time it will take $1000 to accumulate to $1500 if invested at 6%, compounded semiannually:
Find the future value of 1 at the end of n years if the force of interest is ![]() , where t is time:
, where t is time:
Find an expression for the accumulated value of $1000 at the end of 15 years if the effective interest rate is r1 for the first 5 years, r2 for the second 5 years, and r3 for the third 5 years:
If you invest $1000 at 8% per year compounded quarterly, find how much can be withdrawn at the end of every quarter to use up the fund exactly at the end of 10 years:
Find the rate, compounded quarterly, at which $16000 is the present value of a $1000 payment paid at the end of every quarter for 5 years:
Find the accumulated value of a 10-year annuity of $100 per year if the effective rate of interest is 5% for the first 6 years and 4% for the last 4 years:
Find the net present value of a $1000 initial investment producing future incoming cash flows:
Find the internal rate of return of an investment with regular cash flows:
In return for receiving $600 at the end of 8 years, a person pays $100 immediately, $200 at the end of 5 years, and a final payment at the end of 10 years. Find the final payment amount that will make the rate of return on the investment equal to 8% compounded semiannually:
Payments of $100, $200, and $500 are due at the end of years 2, 3, and 8, respectively. Find the point in time where a payment of $800 would be equivalent at 5% interest:
Another method to solve the problem above:
Find the effective rate of interest at which the present value of $2000 at the end of 2 years and $3000 at the end of 4 years will be equal to $4000:
Since a loan's balance at any time is equal to the present value of its remaining future payments, Annuity can be used to create an amortization table:
Properties & Relations (2)
Possible Issues (3)
When finding interest rate solutions to long-term or high-frequency annuities or bonds, FindRoot may be needed instead of Solve:
In order for TimeValue to determine if there are enough rates in a schedule to reach the valuation period, the valuation period must be numeric:
Input numeric valuation period:
Specifying rates by a TimeSeries requires the first time to be 0:
Interactive Examples (1)
Use Manipulate to explore the various dependencies a series of cash flows has on a set of variables:
Text
Wolfram Research (2010), TimeValue, Wolfram Language function, https://reference.wolfram.com/language/ref/TimeValue.html.
CMS
Wolfram Language. 2010. "TimeValue." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TimeValue.html.
APA
Wolfram Language. (2010). TimeValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TimeValue.html