TreeInsert

TreeInsert[tree,child,pos]

inserts child at the position specified by pos in tree.

TreeInsert[tree,child,{pos1,pos2,…}]

inserts child at several positions.

TreeInsert[child,pos]

represents an operator form of TreeInsert that can be applied to a tree.

Details

  • TreeInsert allows insertion of subtrees or general expressions as leaves at any position in a Tree object. »
  • TreeInsert[tree,child,{i,j,…}] inserts the subtree child at position {i,j,…}.
  • TreeInsert can use the position specifications returned by TreePosition as well as extended forms as used in functions such as TreeExtract and TreeReplacePart. »
  • An individual position specification pos can be given as {part1,part2,…}, where part specifications parti include:
  • ithe i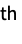^(th) child
    -ithe i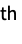^(th) child from the end
    {i1,i2,…}the list of children with part numbers i1, i2, …
    "key"the child whose key is "key"
    Key[k]the child with an arbitrary key k
  • In TreeInsert[tree,child,{p1,p2,…}], {p1,p2,…} is interpreted as a list of individual position specifications if all the pi are lists. Otherwise, {p1,p2,…} will be taken to be an individual position specification. »
  • TreeInsert works on trees containing an Association of subtrees, using the same specification for keys as in Part. »
  • If tree contains an Association of subtrees, TreeInsert[tree,keyvalue,pos] inserts a subtree in the association.
  • If the specified position is of the form "key" or Key[k], then TreeInsert inserts a new subtree before the one corresponding to this key, or overwrites the value if this key is already present.
  • If the key of the subtree to be inserted is already present, then the old subtree with the same key is deleted.
  • TreeInsert[child,pos][tree] is equivalent to TreeInsert[tree,child,pos].
  • TreeInsert has the same options as Tree.

Examples

open allclose all

Basic Examples  (3)

Insert a leaf with the given data into a tree:

Insert a subtree at any position:

Insert at several positions:

Use the operator form of TreeInsert:

Scope  (7)

Associations  (7)

Insert a subtree before a:

Insert several subtrees:

Inserting subtrees with repeating keys overrides earlier values:

Insert a subtree into a tree containing an association by key:

If the key is a string, the Key wrapper is optional:

Insert a subtree into a tree containing an association by key:

Insert a subtree into a tree containing an association by position:

Insert a subtree at a nested position in a tree containing an association:

Insert a subtree at several nested positions in a tree containing an association:

Properties & Relations  (9)

Inserting an expression other than a Tree object is equivalent to inserting a leaf:

The expression x is inserted as the leaf

:

Insert several subtrees using Splice:

Subtrees can be inserted, as well as replaced or deleted:

Construct a tree from the heads in an expression:

TreeInsert inserts a subtree into a tree:

This corresponds to inserting a subexpression into an expression:

Insert can insert subexpressions directly:

For a tree with n children, there are n+1 available positions to insert a new child:

If pos is not a list, pos and {pos} are equivalent specifications:

TreeInsert inserts the new subtree repeatedly if a position is mentioned repeatedly:

TreeInsert can use the lists of positions returned by TreePosition:

These are the subtrees returned by TreeExtract:

TreeInsert[tree,new,{p1,p2,…}] treats {p1,p2,…} as a list of individual position specifications if all the pi are lists:

For {{1,2},{3,4}}, the new subtree is inserted at positions {1,2} and {3,4}:

If any pi is not a list, {p1,p2,…} is treated as a list of part specifications:

For {{{1,2},{3,4}}}, the new subtree is inserted at parts 3 and 4 of parts 1 and 2:

Possible Issues  (3)

TreeInsert[tree,new,{}] does not insert any subtrees because the list of positions is empty:

Subtrees cannot be inserted at the root:

Subtrees cannot be inserted into a leaf:

For an inner node with no children, a child can be inserted at position 1:

Wolfram Research (2021), TreeInsert, Wolfram Language function, https://reference.wolfram.com/language/ref/TreeInsert.html (updated 2023).

Text

Wolfram Research (2021), TreeInsert, Wolfram Language function, https://reference.wolfram.com/language/ref/TreeInsert.html (updated 2023).

CMS

Wolfram Language. 2021. "TreeInsert." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/TreeInsert.html.

APA

Wolfram Language. (2021). TreeInsert. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TreeInsert.html

BibTeX

@misc{reference.wolfram_2024_treeinsert, author="Wolfram Research", title="{TreeInsert}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/TreeInsert.html}", note=[Accessed: 26-April-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_treeinsert, organization={Wolfram Research}, title={TreeInsert}, year={2023}, url={https://reference.wolfram.com/language/ref/TreeInsert.html}, note=[Accessed: 26-April-2024 ]}