TreeInsert
TreeInsert[tree,child,pos]
inserts child at the position specified by pos in tree.
TreeInsert[tree,child,{pos1,pos2,…}]
inserts child at several positions.
TreeInsert[child,pos]
represents an operator form of TreeInsert that can be applied to a tree.
Details and Options

- TreeInsert allows insertion of subtrees or general expressions as leaves at any position in a Tree object. »
- TreeInsert[tree,child,{i,j,…}] inserts the subtree child at position {i,j,…}.
- TreeInsert can use the position specifications returned by TreePosition as well as extended forms as used in functions such as TreeExtract and TreeReplacePart. »
- An individual position specification pos can be given as {part1,part2,…}, where part specifications parti include:
-
i the i 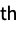 child
child-i the i 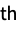 child from the end
child from the end{i1,i2,…} the list of children with part numbers i1, i2, … "key" the child whose key is "key" Key[k] the child with an arbitrary key k - In TreeInsert[tree,child,{p1,p2,…}], {p1,p2,…} is interpreted as a list of individual position specifications if all the pi are lists. Otherwise, {p1,p2,…} will be taken to be an individual position specification. »
- TreeInsert works on trees containing an Association of subtrees, using the same specification for keys as in Part. »
- If tree contains an Association of subtrees, TreeInsert[tree,keyvalue,pos] inserts a subtree in the association.
- If the specified position is of the form "key" or Key[k], then TreeInsert inserts a new subtree before the one corresponding to this key, or overwrites the value if this key is already present.
- If the key of the subtree to be inserted is already present, then the old subtree with the same key is deleted.
- TreeInsert[child,pos][tree] is equivalent to TreeInsert[tree,child,pos].
- TreeInsert has the same options as Tree.
Examples
open allclose allBasic Examples (3)
Insert a leaf with the given data into a tree:
Insert a subtree at any position:
Use the operator form of TreeInsert:
Scope (7)
Associations (7)
Inserting subtrees with repeating keys overrides earlier values:
Insert a subtree into a tree containing an association by key:
If the key is a string, the Key wrapper is optional:
Insert a subtree into a tree containing an association by key:
Insert a subtree into a tree containing an association by position:
Insert a subtree at a nested position in a tree containing an association:
Insert a subtree at several nested positions in a tree containing an association:
Properties & Relations (9)
Inserting an expression other than a Tree object is equivalent to inserting a leaf:
The expression x is inserted as the leaf
:Insert several subtrees using Splice:
Subtrees can be inserted, as well as replaced or deleted:
Construct a tree from the heads in an expression:
TreeInsert inserts a subtree into a tree:
This corresponds to inserting a subexpression into an expression:
Insert can insert subexpressions directly:
For a tree with n children, there are n+1 available positions to insert a new child:
If pos is not a list, pos and {pos} are equivalent specifications:
TreeInsert inserts the new subtree repeatedly if a position is mentioned repeatedly:
TreeInsert can use the lists of positions returned by TreePosition:
These are the subtrees returned by TreeExtract:
TreeInsert[tree,new,{p1,p2,…}] treats {p1,p2,…} as a list of individual position specifications if all the pi are lists:
For {{1,2},{3,4}}, the new subtree is inserted at positions {1,2} and {3,4}:
If any pi is not a list, {p1,p2,…} is treated as a list of part specifications:
For {{{1,2},{3,4}}}, the new subtree is inserted at parts 3 and 4 of parts 1 and 2:
Possible Issues (3)
TreeInsert[tree,new,{}] does not insert any subtrees because the list of positions is empty:
Subtrees cannot be inserted at the root:
Subtrees cannot be inserted into a leaf:
For an inner node with no children, a child can be inserted at position 1:
Text
Wolfram Research (2021), TreeInsert, Wolfram Language function, https://reference.wolfram.com/language/ref/TreeInsert.html (updated 2024).
CMS
Wolfram Language. 2021. "TreeInsert." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/TreeInsert.html.
APA
Wolfram Language. (2021). TreeInsert. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TreeInsert.html