TriangleConstruct
TriangleConstruct[tri,type]
给出三角形 tri 指定类型的结构体.
更多信息




- TriangleConstruct 可以给出 Point、Line、InfiniteLine、Circle 或 Triangle 对象.
- 可用 {p1,p2,p3}、Triangle[{p1,p2,p3}] 或 Polygon[{p1,p2,p3}] 给出三角形 tri.
- 可给出以下类型的点:
-
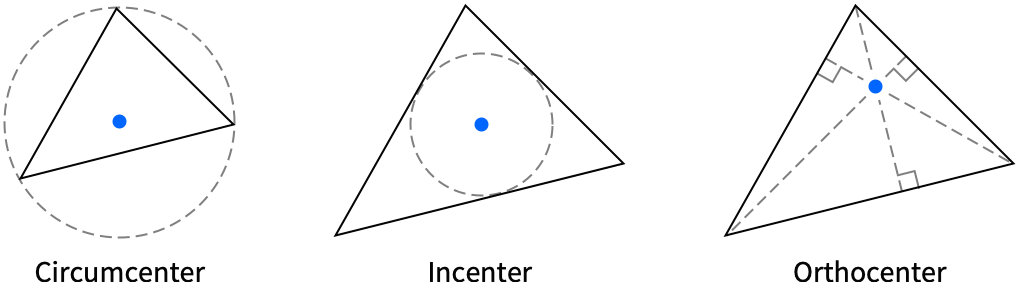
{"AngleBisectingCevianEndpoint",p} 平分顶点 p 的角的塞瓦线段的端点 "Centroid" 几何中心 {"CevianEndpoint",center,p} 穿过顶点 p 和指定中心的塞瓦线段的端点 "Circumcenter" 外接圆的圆心 {"Excenter",p} 与顶点 p 相对的旁切圆的圆心 {"Foot",p} 过顶点 p 的高的垂足 "Incenter" 内切圆的圆心 {"Midpoint",p} 顶点 p 所对边的中点 "NinePointCenter" 九点圆的圆心 "Orthocenter" 垂心 {"SymmedianEndpoint",p} 过顶点 p 的类似中线的端点 "SymmedianPoint" 类似重心 - 可给出以下类型的线:
-
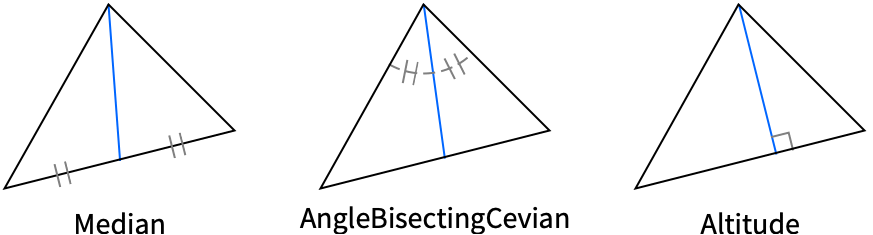
{"Altitude",p} 过顶点 p 的高 {"AngleBisectingCevian",p} 平分顶点 p 的内角的塞瓦线段 {"AngleBisector",p} 顶点 p 的内角平分线 "Boundary" 边界 {"Cevian",center,p} 穿过顶点 p 和指定中心的塞瓦线段 "EulerLine" 欧拉线 {"ExteriorAngleBisector",p} 顶点 p 的外角平分线 {"Median",p} 过顶点 p 的中线 {"OppositeSide",p} 顶点 p 所对的边 {"PerpendicularBisector",p} p 所对的边的中垂线 {"Symmedian",p} 过顶点 p 的类似中线 - 可给出以下类型的圆:
-
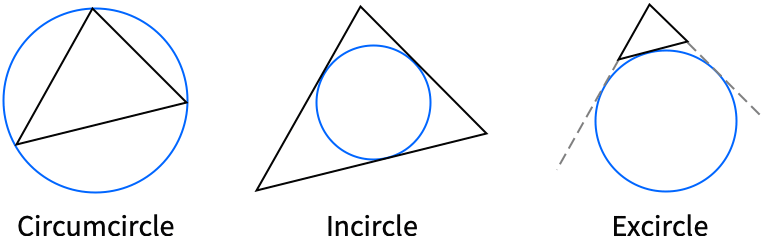
"Circumcircle" 外接圆 {"Excircle",p} 顶点 p 所对的旁切圆 "Incircle" 内切圆 "NinePointCircle" 九点圆 - 可给出以下类型的三角形:
-
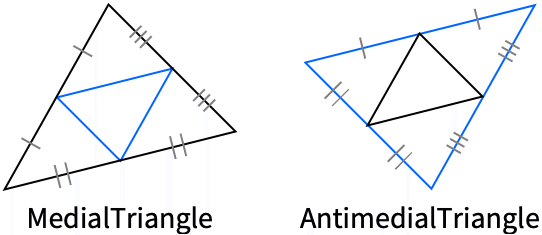
"AntimedialTriangle" 反中点三角形 "MedialTriangle" 中点三角形 "Triangle" 原始三角形 - 在格式 {"type",p} 中,p 可以是 GeometricScene 中的符号点规范,或者是格式 {x,y}、Point[{x,y}] 或顶点的指数 i 的明确点. 当给定短格式 "type",则使用 p2.
- 在格式 {"CevianEndpoint",center,p} 和 {"Cevian",center,p} 中,中心可以给定为中心类型,例如,"Centroid" 或作为点的规范. 当给定短格式 {"CevianEndpoint",center},则使用顶点 p2.
- 在指定顶点 p 的任何形式中,All 值会返回对应顶点的三个值列表.
- TriangleConstruct 可与符号点一起在 GeometricScene 中使用.
范例
打开所有单元关闭所有单元范围 (29)
点 (12)
线 (10)
属性和关系 (28)
角平分线和内心 (5)
TriangleConstruct[{a,b,c},"AngleBisector"] 等价于 AngleBisector[{a,b,c}]:
TriangleConstruct[{a,b,c},"Incircle"] 等价于 Circle[TriangleCenter[{a,b,c},"Incenter"],TriangleMeasurement[{a,b,c},"Inradius"]]:
TriangleConstruct[{a,b,c},"Incircle"] 等价于 Circle@@Insphere[{a,b,c}]:
中线、中点和几何中心 (3)
TriangleConstruct[{a,b,c},"Centroid"] 等价于 Point[RegionCentroid[Triangle[{a,b,c}]]]:
垂直平分线、中点和外心 (5)
TriangleConstruct[{a,b,c},"PerpendicularBisector"] 等价于 PerpendicularBisector[{a,c}]:
TriangleConstruct[{a,b,c},"Circumcircle"] 等价于 Circle[TriangleCenter[{a,b,c},"Circumcenter"],TriangleMeasurement[{a,b,c},"Circumradius"]]:
TriangleConstruct[{a,b,c},"Circumcircle"] 等价于 Circle@@Circumsphere[{a,b,c}]:
外角平分线和旁心 (3)
TriangleConstruct[{a,b,c},"ExteriorAngleBisector"] 等价于 AngleBisector[{a,b,c},"Exterior"]:
TriangleConstruct[{a,b,c},"Excircle"] 等价于 Circle[TriangleCenter[{a,b,c},"Excenter"],TriangleMeasurement[{a,b,c},"Exradius"]]:
九点圆、垂足、中点、垂心 (2)
三角形的九点圆通过高的垂足、边的中点和顶点到垂心的线段的中点:
TriangleConstruct[{a,b,c},"NinePointCircle"] 等价于 Circle[TriangleCenter[{a,b,c},"NinePointCenter"],TriangleMeasurement[{a,b,c},"NinePointRadius"]]:
中点 (1)
TriangleConstruct[{a,b,c},"Midpoint"] 等价于 Point[Midpoint[{a,c}]]:
边界 (1)
TriangleConstruct[{a,b,c},"Boundary"] 等价于 RegionBoundary[Triangle[{a,b,c}]]:
中点三角形和反中点三角形 (2)
TriangleConstruct[{a,b,c},"MedialTriangle"] 等价于 Triangle[TriangleCenter[tri,{"Midpoint",All}]]:
文本
Wolfram Research (2019),TriangleConstruct,Wolfram 语言函数,https://reference.wolfram.com/language/ref/TriangleConstruct.html.
CMS
Wolfram 语言. 2019. "TriangleConstruct." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/TriangleConstruct.html.
APA
Wolfram 语言. (2019). TriangleConstruct. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/TriangleConstruct.html 年