Unequal

lhs!=rhs または lhs≠rhs

左辺 lhs と右辺 rhs が等しいときはFalseを返す．

詳細

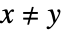  • は，x∖[NotEqual]y またはx != yとしても入力することができる．
  • lhs≠rhs は，数値的な比較または文字列等の要素的なデータの比較により lhs と rhs が等しくないと判断されたときTrueを返す．
  • 近似された数では，最下位の2桁以上が異なる場合に等しくないと判断される．
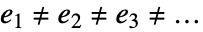  • は，いずれの eiも同値ではないときだけTrueを返す．2≠3≠2->False
  • lhs≠rhs は，ReduceやLogicalExpand等の関数により生成，操作が可能なシンボル的な条件を表す．
  • Unequal[e]は，Trueを与える．
  • 数値的な厳密値に対してUnequalが使われるとき，内部で数値近似が使われ不等関係が確定される．この内部処理には大域変数$MaxExtraPrecisionの設定が影響する．
  • StandardFormにおいて，Unequalは≠と表示される．

予備知識

  • Unequal[expr1,expr2]は，expr1と expr2が数値的に等しくないときはTrueを返し，両者が等しいときはFalseを返し，等価性が実証できない場合は未評価で返す．例えば，Unequal[(1+Sqrt[5])/2,GoldenRatio]はFalseを返し，Unequal[1,2]はTrueを返し，Unequal[1,a]は未評価で返される．Unequal[expr1,expr2]は expr1!=expr2と入力できる．expr1≠expr2のように\[NotEqual]記号を使っても入力できる．引数が複数ある形のUnequal[expr1,expr2,…]（expr1!=expr2!=…と入力）は，式 expriの中に数値的に等しいものがなければTrueを返し，どれか2つが等しい場合はFalseを返し，それ以外の場合は未評価で返される．1引数の形のUnequal[expr]は（多少逆説的ではあるが，1引数形のEqual[expr]がそうであるように）Trueを返す．
  • 機械精度(MachinePrecision)以上の数は，最大で二進表記の最後7桁までが異なっていても等しいとみなされ，それ以外の場合は等しくないとみなされる．機械精度未満の数の等価性は，最低精度の数の精度内での一致に基づいて実証される．例えば，1.01`2!=1はFalseを返すが1.01`3==1はTrueを返す．厳密な数量については，Unequalは数値近似を使って等価性を実証する．これは，大域変数$MaxExtraPrecisionの影響を受ける．
  • Unequalは他の数多くのシンボルと関連している．UnsameQ[expr1,expr2]（expr1=!=expr2と入力）は，expr1と expr2のFullForm表現が異なる場合はTrueを返し，それ以外の場合はFalseを返す．Unequalとは異なり，UnsameQは数の異なる表現を区別する．例えば，UnsameQ[1,1.]とUnsameQ[1.,1.+0.I]はどちらもTrueを返す．UnsameQの動作は，UnsameQが常に評価してTrueまたはFalseを返すのに対しUnequalは等価性が解決しない場合は未評価にとどまることがあるという点でUnequalのそれとも異なる．Equal（expr1==expr2と入力）はUnequalの逆関数である．Unequalは演算子形のUnequalToも持つ．
  • PossibleZeroQを使って，Unequalが未評価で返されるときに与えられた式の値が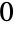になることがあるかどうかを示すことができる．例えば，Unequal[Erf[Log[4]+2Log[Sin[Pi/8]]]-Erf[Log[2-Sqrt[2]]],0]は未評価で返されるが，この第1引数にPossibleZeroQを呼ぶと（0値は厳密には実証できないという有益なメッセージとともに）Trueが返される．Simplify，FullSimplify，RootReduce等の記号簡約子を使って，Unequalにとって不可能な（上に挙げた例を含む）等価性を厳密に実証することができることもある．

例題

すべて開くすべて閉じる

例  (2)

要素が等しくないことが確かな場合はTrueを返し，それ以外の場合は未評価のままになる：

!= または!=で入力する：

スコープ  (11)

数値非等式  (6)

数が等しくないことを確かめる：

最高で二進法での最後の8桁しか違わない近似数は等しいとみなされる：

厳密数の式と近似数を比べる：

2つの厳密な数式を比べる．不等価性の証明には数値テストで十分かもしれない：

等価性の証明には記号的なメソッドが必要である：

Unequalが使う記号メソッドは次がFalseであることを証明するのには不十分である：

RootReduceを使って2つの代数的数が等しくないかどうか判断する：

Unequalが使う数値メソッドは以下の不等価性を証明するのに十分な精度ではない：

RootReduceは2つの代数的数が等しくないことを証明する：

$MaxExtraPrecisionの値を大きくしても不等価性の証明ができるかもしれない：

記号非等式  (5)

この記号的不等価性は常にFalseである：

Unequalは自動的にはこの不等価性を証明しない：

Expandを使ってこれを証明する：

3つ以上の式を比べる：

リストを比べる：

文字列を比べる：

特性と関係  (4)

2引数のUnequalの否定はEqualである：

3引数のUnequalの否定は自動的には簡約されない：

LogicalExpandを使ってこれを2引数のEqualについて表現する：

3引数のUnequalの否定は3引数のEqualと等価ではない：

Unequalは式で表されるオブジェクトの数学的な不等価性をテストする：

UnsameQは式の構造的不等価性をテストする：

Unequalが2つの数式の等価性を判断できないときは，式が未評価で返される：

FullSimplifyは厳密な記号変換を使って不等価性が成立しないことを証明する：

PossibleZeroQは記号的および数値的ヒューリスティックを使って式が零かどうか判断する：

PossibleZeroQが使う数値メソッドは数が零であると不正確に判断することがある：

考えられる問題  (3)

機械精度の近似数の不等価性は微妙なことがある：

余分な桁が等性を乱す：

任意精度の近似数にはこの問題はない：

自動精度追跡機能のお陰で，Unequalには最初の10桁のみを見ればよいことが分かっている：

この場合は，機械数の不等価性テストは期待通りの結果を返す：

この場合の余分な桁はUnequalによって無視される：

Wolfram Research (1988), Unequal, Wolfram言語関数， https://reference.wolfram.com/language/ref/Unequal.html （1996年に更新）.

テキスト

Wolfram Research (1988), Unequal, Wolfram言語関数， https://reference.wolfram.com/language/ref/Unequal.html （1996年に更新）.

CMS

Wolfram Language. 1988. "Unequal." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1996. https://reference.wolfram.com/language/ref/Unequal.html.

APA

Wolfram Language. (1988). Unequal. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Unequal.html

BibTeX

@misc{reference.wolfram_2024_unequal, author="Wolfram Research", title="{Unequal}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/Unequal.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_unequal, organization={Wolfram Research}, title={Unequal}, year={1996}, url={https://reference.wolfram.com/language/ref/Unequal.html}, note=[Accessed: 21-November-2024 ]}