Unequal

lhs!=rhs 或 lhs≠rhs

如果 lhs 和 rhs 相等则返回 False.

更多信息

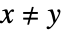  • 可以输入为 x∖[NotEqual]y 或 x != y.
  • 如果 lhs 和 rhs 通过数或其它原字符（例如字符串）的比较确定为不相等，则 lhs≠rhs 返回 True.
  • 如果它们除最后两个数字外不同，近似数被认为是不相等的.
  • 仅当 ei 都不相等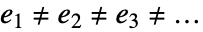， 给出 True. 2≠3≠2->False.
  • lhs≠rhs 表示能用类似函数 Reduce 和 LogicalExpand 产生和处理的符号条件.
  • Unequal[e] 给出 True.
  • 对精确数值量，Unequal 内部使用数值近似值建立不等式. 这个过程受到全局变量 $MaxExtraPrecision 设置的影响.
  • 在 StandardForm 中，Unequal 用 ≠ 输出.

背景

  • Unequal[expr1,expr2] 返回 True，如果 expr1 和 expr2 是数值上不等，如果相等，则为 False，如果不能建立相等性，则不被计算. 例如，Unequal[(1+Sqrt[5])/2,GoldenRatio] 返回 False，Unequal[1,2] 返回 True，Unequal[1,a] 返回未被计算. Unequal[expr1,expr2] 可以用 expr1!=expr2 输入或使用 \[NotEqual] 字符作为 expr1≠expr2. 多变量形式 Unequal[expr1,expr2,…]，也可以输入为 expr1!=expr2!=…，如果没有表达式 expri 是数值相等，则返回 True，如果任何两个相等，则 False，否则，不计算. 单变量形式 Unequal[expr] 返回 True（有点矛盾的是，单变量形式 Equal[expr] 也是这个结果）.
  • 机器精度 (MachinePrecision) 或更大的数如果只差最多最后 7 个二进制数字则认为是相等的，否则，不等. 低于机器精度的数值相等性建立在最低精度数的精度内. 例如，1.01`2!=1 返回 False，但是 1.01`3==1 返回 True. 对于确切的数值量，Unequal 使用数值近似建立不等性，其可以受到全局变量 $MaxExtraPrecision 值的影响.
  • Unequal 与其他符号相关. UnsameQ[expr1,expr2]（可以输入为 expr1=!=expr2）返回 True，如果expr1 和 expr2 的基本 FullForm 表示不同，否则，返回 False. 与 Unequal 相比，UnsameQ 区分不同的数值表示；例如，UnsameQ[1,1.] 和 UnsameQ[1.,1.+0.I] 均返回 True. UnsameQ 的行为也与 Unequal 不同，UnsameQ 总是计算为 True 或 False，其中，如果不能解决相等性，Unequal 可能保持不被计算. Equal（可以输入为 expr1==expr2）是 Unequal 的反. Unequal 还有运算符形式 UnequalTo.
  • 如果在某些 Unequal 返回未被计算的情况下，给定的表达式有值 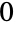，则可以使用 PossibleZeroQ 指明. 例如，Unequal[Erf[Log[4]+2Log[Sin[Pi/8]]]-Erf[Log[2-Sqrt[2]]],0] 返回被计算的，其中，在第一个变量中调用 PossibleZeroQ，返回 True（和充满信息的消息表明零值不能被严格建立）. 有时当 Unequal 不能时，符号简化像 Simplify、FullSimplify 和 RootReduce 可用于严格建立相等性（包括刚才给出的例子）.

范例

打开所有单元关闭所有单元

基本范例  (2)

如果元素确定不相等，返回 True，其它方式不计算：

输入 !=或 !=：

范围  (11)

数值不等式  (6)

测试数的不等性：

最后8位二进制数不相同的近似数被认为是相等的：

将明确的数值表达式和一个近似数相比较：

比较两个明确数值表达式；一个数值测试可能不足以证明不等性：

证明不等式需要符号方法：

Unqual 使用的符号方法不足以证明这个 False：

用 RootReduce 确定两个代数数是否不相等：

Unqual 使用的数值方法没有提供足够的精度来证明这个不等性：

RootReduce 证明两个代数数是不相等的：

增加 $MaxExtraPrecision 可能也允许证明不等性：

符号不等式  (5)

这个符号不等性通常是 False：

Unqual 不自动证明这个不等性：

用 Expand 证明它：

比较更多的表达式：

比较列表：

比较字符串：

属性和关系  (4)

二元 Unequal 的否定式 Equal：

不能自动化简三元 Unequal 的否定式：

用 LogicalExpand 按二元 Equal 的项来表示：

三元 Unequal 的否定不等于三元 Equal：

Unqual 测试表达式表示对象的数学不等性：

UnsameQ 测试表达式的语法不等性：

当 Unequal 不能确定两个数值表达式是否相等时，返回不变化的结果：

FullSimplify 用明确的符号转换来反证这个不等性：

PossibleZeroQ 用数值和符号的试探法来确定一个表达式是否为零：

PossibleZeroQ 使用的数值方法可能错误的判断一个数为零：

可能存在的问题  (3)

机器精度近似数的不等性是很敏感的：

额外的数字破坏了相等性：

任意精度的近似数没有这个问题：

因为自动精度的追踪，Unequal 仅识别前10位数：

在这个例子中，机器数的不等性测试给出预期的结果：

这个例子中的额外数字被 Unequal 忽视：

Wolfram Research (1988)，Unequal，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Unequal.html （更新于 1996 年）.

文本

Wolfram Research (1988)，Unequal，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Unequal.html （更新于 1996 年）.

CMS

Wolfram 语言. 1988. "Unequal." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 1996. https://reference.wolfram.com/language/ref/Unequal.html.

APA

Wolfram 语言. (1988). Unequal. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Unequal.html 年

BibTeX

@misc{reference.wolfram_2024_unequal, author="Wolfram Research", title="{Unequal}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/Unequal.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_unequal, organization={Wolfram Research}, title={Unequal}, year={1996}, url={https://reference.wolfram.com/language/ref/Unequal.html}, note=[Accessed: 21-November-2024 ]}