WarpingDistance[s1,s2]
gives the dynamic time warping (DTW) distance between sequences s1 and s2.
WarpingDistance[s1,s2,win]
uses a window specified by win for local search.


WarpingDistance
WarpingDistance[s1,s2]
gives the dynamic time warping (DTW) distance between sequences s1 and s2.
WarpingDistance[s1,s2,win]
uses a window specified by win for local search.
Details and Options



- WarpingDistance gives the minimal distance for any correspondence between the reference sequence s1 and the query sequence s2.
- The distance is given by
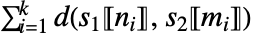 , where s1〚ni〛 and s2〚mi〛 are corresponding elements.
, where s1〚ni〛 and s2〚mi〛 are corresponding elements. - Compute the effective correspondence using WarpingCorrespondence.
- The sequences si can be lists of numeric or Boolean scalars or vectors.
- Possible settings for the search window win are:
-

Automatic a full search 
r a slanted band window of radius 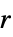

{"SlantedBand",r} a slanted band window of radius 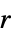

{"Band",r} band window of radius 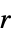 (Sakoe-Chiba)
(Sakoe-Chiba)
{"Parallelogram",a} parallelogram window placed at origin with slopes 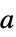 and
and 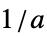 (Itakura)
(Itakura) - A smaller
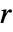 typically gives a faster but less optimal result. If
typically gives a faster but less optimal result. If ![max(Length[s_1],Length[s_2])<=2 r +1 max(Length[s_1],Length[s_2])<=2 r +1](Files/WarpingDistance.en/13.png) , then
, then 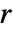 has no effect.
has no effect. - The following options are supported:
-
DistanceFunction Automatic the distance function to be used Method Automatic the variant of DTW to use - WarpingDistance accepts a DistanceFunctiond option with settings:
-
Automatic automatically determine distance function EuclideanDistance Euclidean distance ManhattanDistance Manhattan or "city block" distance BinaryDistance 0 if elements are equal; 1 otherwise ChessboardDistance Chebyshev or sup norm distance SquaredEuclideanDistance squared Euclidean distance NormalizedSquaredEuclideanDistance normalized squared Euclidean distance CosineDistance angular cosine distance CorrelationDistance correlation coefficient distance BrayCurtisDistance Total[Abs[u-v]]/Total[Abs[u+v]] CanberraDistance Total[Abs[u-v]/(Abs[u]+Abs[v])] MatchingDissimilarity matching dissimilarity between Boolean vectors - By default, the following distance functions are used:
-
EuclideanDistance numeric data MatchingDissimilarity Boolean data - Using Method->Automatic, all elements of s2 are matched with all elements of s1.
- Using Method->{"MatchingInterval"match}, s2 can be matched with a subsequence of s1. Possible settings for match include:
-
Automatic a full match "Flexible" flexible at both ends "FlexibleEnd" flexible only at the end of the interval
Examples
open all close allBasic Examples (1)
Scope (10)
Data (7)
Find the time warping distance between two real-valued vectors:
Find the time warping distance between two sequences of 2D points:
Show the correspondence between the sequences:
Find the time warping distance between two Boolean vectors:
Sequences of Boolean-valued vectors:
Sequences of quantities with compatible units:
All units are converted to base SI units:
Two-dimensional quantity arrays:
Find the distance between a sequence of quantities and a sequence of scalars:
The scalars are interpreted as if they had a compatible unit from SI base units:
Search Window (3)
By default, the search is not locally constrained:
Specify a radius for the search window:
Increase the radius to find a more optimal alignment:
A window size is interpreted as the radius of a slanted band window:
Use a parallelogram of slope 3:
For signals of equal length, the "Band" window is equivalent to the "SlantedBand" window:
Generalizations & Extensions (1)
Compute DTW-Delta (or DTW-D) by normalizing DTW by the Euclidean distance of sequences:
Comparing a sine wave, a distorted sine wave, and a random noise using DTW:
Using regular DTW, the sine wave seems to be more similar to the random noise:
Using DTW-Delta, the sine wave is more similar to the distorted sine wave:
Options (6)
DistanceFunction (5)
With Boolean sequences, WarpingDistance uses MatchingDissimilarity:
Compare two sequences using different distance functions:
In case of one-dimensional signals, some distance functions are equivalent:
In case of one-dimensional signals, NormalizedSquaredEuclideanDistance and CorrelationDistance always return 0:
For signals containing one element, time warping distance is equal to the distance between elements:
Applications (6)
Cluster time series of normalized stock values:
Find the nearest stock based on normalized stock values:
Find the capital city in the EU that had the most similar temperature to Chicago over the last year. Use WarpingDistance to determine the similarity between temperature sequences:
Get the temperature for all capital cities in the European Union:
Find the capital city that has the most similar temperatures to Chicago:
Compute pairwise distances between temperature time series of all EU capitals:
Visualize the temperature similarity using a previously computed distance matrix:
Compare daily mean humidity for some cities in 2014:
Extract humidity of the cities:
Properties & Relations (8)
The two sequences need not have the same length:
The distance between two equal sequences is always 0:
Relation with WarpingCorrespondence:
Find the time warped sequences using the correspondence:
WarpingDistance gives the sum of all the distances between corresponding elements:
Smaller window radius results in faster computation:
However, using smaller radius may lead to a less optimal alignment, resulting in higher distance values:
WarpingDistance is a symmetric function:
The "triangle inequality" does not hold:
Dynamic time warping is not translation invariant:
Canonical time warping is translation invariant:
The time warping distance increases for longer signals:
Normalization allows a more reasonable comparison:
Dividing by the length of the correspondence path is also a common way of normalization:
Possible Issues (3)
The search window specified may be too narrow to contain a correspondence path. In that case it will be automatically widened:
Two long, similar signals could have a higher distance compared to two short, dissimilar signals:
Comparing two short, random sequences, which gives a relatively smaller distance:
Divide by the length of signals:
Divide by the length of the correspondence path:
Quantities in input sequences must have compatible units:
Related Guides
History
Text
Wolfram Research (2016), WarpingDistance, Wolfram Language function, https://reference.wolfram.com/language/ref/WarpingDistance.html.
CMS
Wolfram Language. 2016. "WarpingDistance." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WarpingDistance.html.
APA
Wolfram Language. (2016). WarpingDistance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WarpingDistance.html
BibTeX
@misc{reference.wolfram_2025_warpingdistance, author="Wolfram Research", title="{WarpingDistance}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/WarpingDistance.html}", note=[Accessed: 25-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_warpingdistance, organization={Wolfram Research}, title={WarpingDistance}, year={2016}, url={https://reference.wolfram.com/language/ref/WarpingDistance.html}, note=[Accessed: 25-January-2026]}