WinsorizedMean

WinsorizedMean[list,f]

给出把最小和最大的 f（比例）元素用剩下元素的极值替换后 list 中元素的均值.

WinsorizedMean[list,{f1,f2}]

给出把最小的 f1（比例）元素和的最大的 f2（比例）元素用剩下元素的极值替换后列表中元素的均值.

WinsorizedMean[list]

给出经 5% 缩尾处理后的均值 WinsorizedMean[list,0.05].

WinsorizedMean[dist,…]

给出单变量分布 dist 经缩尾处理后的均值.

更多信息

  • 由于偏离程度大的极值被偏离程度较小的极值所替代，WinsorizedMean 给出对均值的稳健估计.
  • 缩尾比例由参数 f1 和 f2 确定，表示把最小的 f1（比例）元素和的最大的 f2（比例）元素替换成剩下元素的极值.
  • WinsorizedMean[list,{f1,f2}] 给出 Clip[list,{z1,z2}] 的均值，其中 z1 等于 RankedMin[list,1+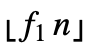]，z2 等于 RankedMax[list,1+]，n 等于 list 的长度. »
  • 一元 WeightedData data 的 WinsorizedMean 给出删失 data 的加权均值. »
  • WinsorizedMean[{{x1,y1,…},{x2,y2,…},…},f] 给出 {WinsorizedMean[{x1,x2,…},f],WinsorizedMean[{y1,y2,…},f],…}. »
  • 对于单变量分布 dist，WinsorizedMean[dist,{f1,f2}] 给出 Mean[CensoredDistribution[Quantile[dist,{f1,1-f2}],dist]]. »

范例

打开所有单元关闭所有单元

基本范例  (4)

去掉极值后的缩尾均值：

去掉最小极值后的缩尾均值：

日期列表的缩尾均值：

符号分布的缩尾均值：

范围  (11)

数据  (10)

精确输入给出精确输出：

近似输入给出近似输出：

矩阵的缩尾均值按列给出均值：

大型数组的缩尾均值：

可以像对稠密数组一样使用 SparseArray 数据：

一元 WeightedData 的 WinsorizedMean：

与未加权数据的均值相比较：

TimeSeries 的缩尾均值：

缩尾均值只取决于数值：

可对含有量的数据求缩尾均值：

计算日期的缩尾均值：

计算时间的缩尾均值：

以不同的时区规范给出的时间：

分布  (1)

单变量分布的缩尾均值：

应用  (3)

在异常值出现的情况下，计算位置的稳健估计值：

极值对均值的影响很大：

仿真带有重尾测量噪声的轨迹：

基本信号和带有噪声的仿真路径：

用移动 WinsorizedMean 平滑轨迹：

增大区块 (block) 的大小使得轨迹更平滑：

求一个班的孩子们的身高的缩尾均值：

5% 缩尾均值：

比较几个缩尾均值：

绘制缩尾均值作为比例参数的函数的曲线：

属性和关系  (5)

0% WinsorizedMean 等价于 Mean：

当 f 趋于 1/2 时 WinsorizedMean 趋近于 Median：

一个分布的 WinsorizedMean 是它的 CensoredDistribution 的均值：

适当界限下的 CensoredDistribution 的均值：

样本的 WinsorizedMean 给出对删失分布的均值的估计：

适当界限下的 CensoredDistribution 的均值：

TrimmedMean 会丢弃一定分位数之上的数据，然后再计算样本均值：

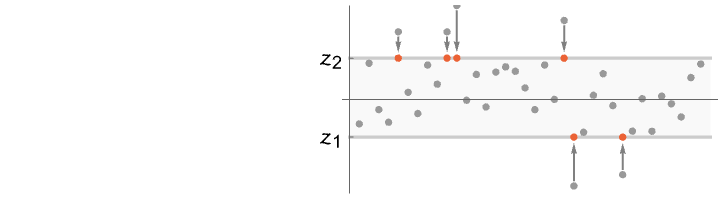
WinsorizedMean 剪切一定分位数之上的数据，然后再计算样本均值：

绘制排序后的数据与经过截断（移除元素）或剪切（较大极值被替换）处理的数据：

可能存在的问题  (1)

WinsorizedMean 只接受数值型输入：

Wolfram Research (2017)，WinsorizedMean，Wolfram 语言函数，https://reference.wolfram.com/language/ref/WinsorizedMean.html （更新于 2024 年）.

文本

Wolfram Research (2017)，WinsorizedMean，Wolfram 语言函数，https://reference.wolfram.com/language/ref/WinsorizedMean.html （更新于 2024 年）.

CMS

Wolfram 语言. 2017. "WinsorizedMean." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/WinsorizedMean.html.

APA

Wolfram 语言. (2017). WinsorizedMean. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/WinsorizedMean.html 年

BibTeX

@misc{reference.wolfram_2024_winsorizedmean, author="Wolfram Research", title="{WinsorizedMean}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/WinsorizedMean.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_winsorizedmean, organization={Wolfram Research}, title={WinsorizedMean}, year={2024}, url={https://reference.wolfram.com/language/ref/WinsorizedMean.html}, note=[Accessed: 21-November-2024 ]}