WishartMatrixDistribution
WishartMatrixDistribution[ν,Σ]
represents a Wishart matrix distribution with ν degrees of freedom and covariance matrix Σ.
Details

- WishartMatrixDistribution is the distribution of the sample covariance from ν independent realizations of a multivariate Gaussian distribution with covariance matrix Σ when the degrees of freedom parameter ν is an integer.
- WishartMatrixDistribution is also known as Wishart–Laguerre ensemble.
- The probability density for a symmetric matrix
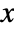 in a Wishart matrix distribution is proportional to
in a Wishart matrix distribution is proportional to 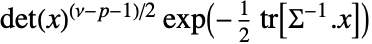 , where
, where 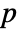 is the size of matrix Σ.
is the size of matrix Σ. - The covariance matrix
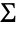 can be any positive definite symmetric matrix of dimensions
can be any positive definite symmetric matrix of dimensions 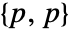 and ν can be any real number greater than
and ν can be any real number greater than 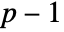 .
. - WishartMatrixDistribution can be used with such functions as MatrixPropertyDistribution, EstimatedDistribution, and RandomVariate.
Examples
open allclose allBasic Examples (3)
Generate a pseudorandom matrix:
Check that it is symmetric and positive definite:
Sample eigenvalues of a Wishart random matrix using MatrixPropertyDistribution:
Scope (6)
Generate a single pseudorandom matrix:
Generate a set of pseudorandom matrices:
Compute statistical properties numerically:
Numerically approximate expectation of the largest matrix eigenvalue ![]() :
:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare LogLikelihood for both distributions:
Applications (2)
When n and p (the dimension of the covariance matrix Σ) are both large, the scaled largest eigenvalue of a matrix from a Wishart ensemble with identity covariance is approximately distributed as a Tracy–Widom distribution:
Sample the scaled largest eigenvalue:
Check goodness of fit with TracyWidomDistribution:
Algebraically independent components of a symmetric Wishart matrix have a known PDF:
Build the distribution of independent components of a ![]() Wishart matrix:
Wishart matrix:
Find the joint distribution of a diagonal element:
Use MatrixPropertyDistribution to sample diagonal elements of Wishart matrices:
Properties & Relations (4)
Use MatrixPropertyDistribution to represent the scaled eigenvalues of a Wishart random matrix with identity covariance:
The limiting distribution of eigenvalues follows MarchenkoPasturDistribution:
Compare the histogram of the eigenvalues with the PDF:
The expression ![]() , where
, where ![]() and
and ![]() are, respectively, an independent Gaussian vector and Wishart matrix, follows HotellingTSquareDistribution:
are, respectively, an independent Gaussian vector and Wishart matrix, follows HotellingTSquareDistribution:
Use MatrixPropertyDistribution to sample expressions ![]() :
:
Diagonal elements of a Wishart random matrix each follow a scaled χ2 distribution:
Test against applicably scaled χ2 distributions:
Diagonal elements are not independent:
For any nonzero vector ![]() and Wishart matrix
and Wishart matrix ![]() with scale matrix
with scale matrix ![]() ,
, ![]() is χ2 distributed:
is χ2 distributed:
Text
Wolfram Research (2015), WishartMatrixDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/WishartMatrixDistribution.html (updated 2017).
CMS
Wolfram Language. 2015. "WishartMatrixDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/WishartMatrixDistribution.html.
APA
Wolfram Language. (2015). WishartMatrixDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WishartMatrixDistribution.html