MarchenkoPasturDistribution[λ,σ]
represents a Marchenko–Pastur distribution with asymptotic ratio ![]() and scale parameter
and scale parameter ![]() .
.
MarchenkoPasturDistribution[λ]
represents a Marchenko–Pastur distribution with unit scale parameter.


MarchenkoPasturDistribution
MarchenkoPasturDistribution[λ,σ]
represents a Marchenko–Pastur distribution with asymptotic ratio ![]() and scale parameter
and scale parameter ![]() .
.
MarchenkoPasturDistribution[λ]
represents a Marchenko–Pastur distribution with unit scale parameter.
Details
- MarchenkoPasturDistribution is the limiting spectral density of random matrices from WishartMatrixDistribution.
- The derivative of cumulative distribution function at
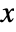 in a Marchenko–Pastur distribution is proportional to
in a Marchenko–Pastur distribution is proportional to 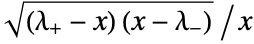 with
with 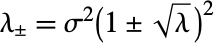 for
for 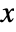 between
between 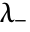 and
and 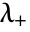 .
. - Marchenko–Pastur distribution has a point mass at
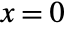 with probability
with probability 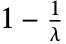 when
when 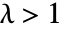 .
. - MarchenkoPasturDistribution allows
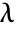 and
and 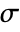 to be any positive real numbers.
to be any positive real numbers. - MarchenkoPasturDistribution allows σ to be a quantity of any unit dimension, and λ to be a dimensionless quantity. »
- MarchenkoPasturDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Examples
open all close allBasic Examples (3)
Scope (7)
Generate a sample of pseudorandom numbers from a Marchenko–Pastur distribution with ![]() :
:
Compare its histogram to the PDF:
Generate a sample of pseudorandom numbers from a Marchenko–Pastur distribution with ![]() :
:
Compare its cumulative histogram to the CDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the cumulative histogram of the sample with the CDF of the estimated distribution:
Skewness and kurtosis depend only on ![]() :
:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Closed form for symbolic order:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (1)
Use MatrixPropertyDistribution to represent the eigenvalues of a Wishart random matrix with identity covariance:
The spectral density converges to the pdf of MarchenkoPasturDistribution[λ] in the limit of large ![]() and
and ![]() with the finite ratio
with the finite ratio ![]() :
:
Properties & Relations (3)
MarchenkoPasturDistribution is closed under scaling by a positive factor:
MarchenkoPasturDistribution has an atomic weight at 0 when ![]() :
:
MarchenkoPasturDistribution is the limiting distribution of eigenvalues of Wishart matrices. The atomic weight at ![]() occurs when the Wishart matrix is singular. Generate a singular Wishart matrix with identity covariance and compute the scaled eigenvalues:
occurs when the Wishart matrix is singular. Generate a singular Wishart matrix with identity covariance and compute the scaled eigenvalues:
Fit MarchenkoPasturDistribution to the eigenvalues:
Compare the cumulative histogram of the eigenvalues with the CDF:
Possible Issues (1)
Marchenko–Pastur distribution with ![]() is a mixed type distribution, which is neither continuous nor discrete:
is a mixed type distribution, which is neither continuous nor discrete:
The CDF for such Marchenko–Pastur distributions is discontinuous at ![]() :
:
The probability density function for Marchenko–Pastur distribution with ![]() is not defined, and PDF returns unevaluated:
is not defined, and PDF returns unevaluated:
Differentiation of the CDF results in a function that does not integrate to one:
Computations with mixed type distributions are fully supported. Compute special moments:
Related Guides
Text
Wolfram Research (2015), MarchenkoPasturDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/MarchenkoPasturDistribution.html (updated 2016).
CMS
Wolfram Language. 2015. "MarchenkoPasturDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/MarchenkoPasturDistribution.html.
APA
Wolfram Language. (2015). MarchenkoPasturDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MarchenkoPasturDistribution.html
BibTeX
@misc{reference.wolfram_2025_marchenkopasturdistribution, author="Wolfram Research", title="{MarchenkoPasturDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MarchenkoPasturDistribution.html}", note=[Accessed: 14-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_marchenkopasturdistribution, organization={Wolfram Research}, title={MarchenkoPasturDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/MarchenkoPasturDistribution.html}, note=[Accessed: 14-December-2025]}