WishartMatrixDistribution[ν,Σ]
表示一个自由度为 ν 、协方差矩阵为 Σ 的 Wishart 矩阵分布.


WishartMatrixDistribution
WishartMatrixDistribution[ν,Σ]
表示一个自由度为 ν 、协方差矩阵为 Σ 的 Wishart 矩阵分布.
更多信息

- WishartMatrixDistribution 是当自由度参数 ν 为整数时,协方差矩阵为 Σ 的多变量高斯分布的 ν 个独立实现的样本协方差的分布.
- WishartMatrixDistribution 也称作 Wishart–Laguerre 系综.
- Wishart 矩阵分布中的对称矩阵
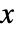 的概率密度与
的概率密度与 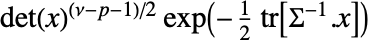 成正比,其中
成正比,其中 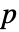 是矩阵 Σ 的大小.
是矩阵 Σ 的大小. - 协方差矩阵
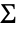 可以是任意维数为
可以是任意维数为 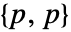 正定对称矩阵,而且 ν 可以是任意大于
正定对称矩阵,而且 ν 可以是任意大于 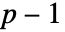 的实数.
的实数. - WishartMatrixDistribution 可与诸如 MatrixPropertyDistribution、EstimatedDistribution 和 RandomVariate 这样的函数一起使用.
范例
打开所有单元 关闭所有单元基本范例 (3)
范围 (6)
比较两个分布的 LogLikelihood:
应用 (2)
当 n 和 p(协方差矩阵 Σ 的维度)都很大时,有相同协方差的 Wishart 系综矩阵的已缩放最大特征值大致符合 Tracy-Widom 分布:
检查与 TracyWidomDistribution 的拟合优度:
对称 Wishart 矩阵的代数独立分量有已知的 PDF:
使用 MatrixPropertyDistribution 对 Wishart 矩阵的对角线元素进行抽样:
属性和关系 (4)
使用 MatrixPropertyDistribution 表示有同一协方差的 Wishart 随机矩阵的缩放过的特征值:
特征值的极限分布遵循 MarchenkoPasturDistribution:
将特征值的直方图与 PDF 相比较:
表达式 ![]() 满足 HotellingTSquareDistribution,其中
满足 HotellingTSquareDistribution,其中 ![]() 和
和 ![]() 分别是独立高斯向量和 Wishart 矩阵:
分别是独立高斯向量和 Wishart 矩阵:
使用 MatrixPropertyDistribution 对表达式 ![]() 进行抽样:
进行抽样:
文本
Wolfram Research (2015),WishartMatrixDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/WishartMatrixDistribution.html (更新于 2017 年).
CMS
Wolfram 语言. 2015. "WishartMatrixDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2017. https://reference.wolfram.com/language/ref/WishartMatrixDistribution.html.
APA
Wolfram 语言. (2015). WishartMatrixDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/WishartMatrixDistribution.html 年
BibTeX
@misc{reference.wolfram_2025_wishartmatrixdistribution, author="Wolfram Research", title="{WishartMatrixDistribution}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/WishartMatrixDistribution.html}", note=[Accessed: 27-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_wishartmatrixdistribution, organization={Wolfram Research}, title={WishartMatrixDistribution}, year={2017}, url={https://reference.wolfram.com/language/ref/WishartMatrixDistribution.html}, note=[Accessed: 27-February-2026]}