"KMeans" (機械学習メソッド)

詳細とサブオプション

  • "KMeans"は，古典的で単純な重心に基づくクタスタリング法である．"KMeans"は，クラスタのサイズが同じ位で重心の周りに局所的かつ等方的に分布している場合に使える．クラスタのサイズが大きく異なっていたり，異方性であったり，絡み合っていたり，外れ値が存在したりする場合は，"KMeans"が返す結果はあまりよくない可能性がある．
  • 次のプロットは，"KMeans"法をトイデータ集合に適用した結果を示している．
  • "KMeans"法は，k 個のクラスタを定義している k 個の重心を求めることを目的としている．各データ点は最近傍の重心に割り当てられる．ある重心に割り当てられたすべての点によってクラスタが形成される．
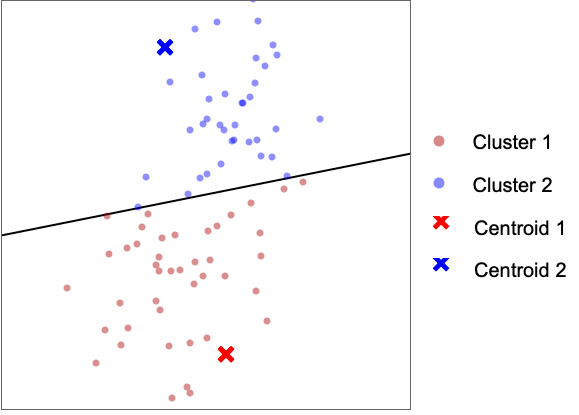
  • 最良の k 個の重心を求める手続きは反復的である．探索はランダムな重心を用いて，各点を最も近くにある重心に割り当てることから始まる：
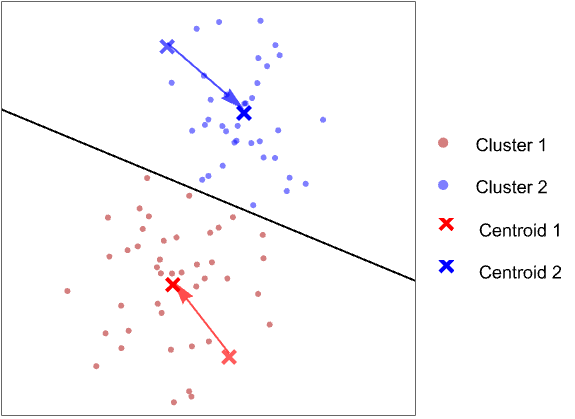
  • すべてのクラスタが定義されると，各クラスタの平均が新たな重心となる：
  • この手続きはクラスタが変化しなくなるまで繰り返される．この反復的な手続きは「硬いEM」（硬い期待値最大化，hard Expectation Maximization）と呼ばれることがある．
  • "KMeans"法は球面共分散のある（つまり，すべてのクラスタが等方性で同じサイズである）"GaussianMixture"に似ている．
  • 初期重心はランダムに選ばれるので，評価によって結果が異なることがある．
  • サブオプション"InitialCentroids"を使って初期重心をデータ点のリストとして指定できる．
  • 次は，使用可能なサブオプションである．
  • "InitialCentroids" Automatic初期重心のリスト

例題

すべて開くすべて閉じる

例  (3)

"KMeans"クラスタリング法を使って近くの値の厳密に4つのクラスタを求める：

ランダムな2Dベクトルを作成する：

"KMeans"法を使って計算されたクラスタをプロットする：

ClassifierFunction を文字列のリストで訓練する：

クラスタ割当てを求め，要素をクラスタによってまとめる：

オプション  (3)

DistanceFunction  (1)

マンハッタン距離を使ってデータをクラスタ化する：

"InitialCentroids"  (2)

ランダムな100色のリストを生成する：

"KMeans"法を使って，重心の初期構成を指定せずに色をクラスタ化する：

"KMeans"法を使って，重心として使用する初期色を指定する：

ランダムな2Dベクトルを作成する：

"KMeans"法を使って"InitialCentroids"を変えることでデータの異なるクラスタリングを求める：

考えられる問題  (1)

ノイズがある2Dの月の形の訓練データ集合と検証データ集合を，作成して可視化する：

"KMeans"を使ってClassifierFunctionを2つのクラスタについて訓練し，検証集合中のクラスタを求める：

クラスタを可視化すると，絡み合っているクラスタについては"KMeans"のパフォーマンスがあまりよくないことが分かる：