"KMedoids" (Machine Learning Method)
- Method for FindClusters, ClusterClassify and ClusteringComponents.
- Partitions data into
 clusters of similar elements using a k-medoids clustering algorithm.
clusters of similar elements using a k-medoids clustering algorithm.
Details & Suboptions
- The "KMedoids" method, also known as Partitioning Around Medoids (PAM), is a simple and fast centroid-based method. "KMedoids" is good when clusters have similar sizes and are locally distributed around their centroid (a.k.a. medoids). When clusters have very different sizes, are intertwined, or when outliers are present, it is likely that "KMedoids" will give poor results.
- The following plots show the results of the "KMedoids" method applied to toy datasets:
-

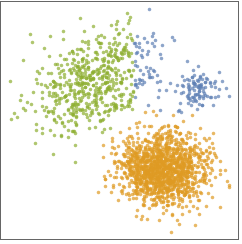
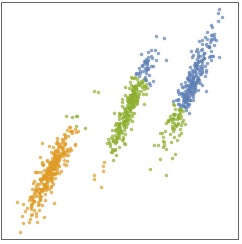

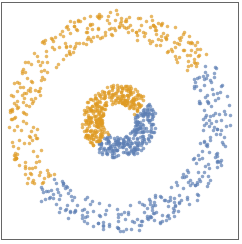
- The "KMedoids" method aims to find k medoids defining k clusters. Each data point is assigned to its nearest medoid. All points assigned to a given medoid are forming a cluster.
- The procedure to find the best k medoids is the same as "KMeans", except that the medoids are not defined as the mean of a cluster. Instead, a cluster medoid is defined as the data point in the cluster that is the most central, that is, the data point whose average distance to other points in the cluster is minimal. Because "KMedoids" does not compute means like "KMeans", it can be used in non-numeric spaces (a distance function is sufficient).
- Since the initial centroids are chosen randomly, results might differ upon evaluation.
- The suboption "InitialCentroids" can be used to specify the initial centroids as a list of data points. Each initial centroid must match an existing data point.
- The following suboption can be given:
-
"InitialCentroids" Automatic a list of initial centroids
Examples
open all close allBasic Examples (3)
Find exactly four clusters of nearby values using the "KMedoids" clustering method:
Find clusters in data found using the "KMedoids" method:
Train a ClassifierFunction on a list of strings:
Find the cluster assignments and gather the elements by their cluster:
Options (3)
Possible Issues (1)
Create and visualize noisy 2D moon-shaped training and test datasets:
Train a ClassifierFunction using "KMedoids" for two clusters and find clusters in the test set:
Visualizing clusters indicates that "KMedoids" performs poorly on intertwined clusters: