"KMeans" （机器学习方法）

详细信息和子选项

  • "KMeans" 是一种经典、简单、基于质心的聚类方法. "KMeans" 适用于集群具有相似大小并且围绕其质心局部且各向同性分布的情况. 当聚类大小迥异、各向异性、相互交织或存在异常值时，"KMeans" 很可能会给出较差的结果.
  • 以下各图显示了 "KMeans" 方法应用于玩具数据集的结果：
  • "KMeans" 方法旨在找到定义 k 个簇的 k 个质心. 每个数据点都分配给距它最近的质心. 分配给给定质心的全体点形成一个簇.
  • 寻找 k 个最佳质心的过程是迭代式的. 首先使用随机质心并将每个点分配给距它最近的质心：
  • 一旦所有簇均被定义，每个簇的平均值就变成了一个新的质心：
  • 不断重复此过程，直到簇保持不变. 这个迭代过程有时被称为硬期望最大化（“hard EM”，即 hard Expectation Maximization）.
  • "KMeans" 方法类似于具有球形协方差的 "GaussianMixture"（即所有簇都是各向同性并且大小相同）.
  • 由于初始质心是随机选择的，因此每次运算的结果可能会有所不同.
  • 子选项 "InitialCentroids" 可用于将初始质心指定为数据点列表.
  • 可以给出以下子选项：
  • "InitialCentroids" Automatic初始质心列表

范例

打开所有单元关闭所有单元

基本范例  (3)

使用 "KMeans" 聚类方法找到附近值的恰好四个聚类：

创建随机二维向量：

使用 "KMeans" 方法绘制计算的簇：

在一个字符串列表上训练 ClassifierFunction：

查找簇的分配并按簇集合元素：

选项  (3)

DistanceFunction  (1)

使用曼哈顿距离的聚类数据：

"InitialCentroids"  (2)

生成 100 种随机颜色的列表：

使用 "KMeans" 方法在不指定质心初始配置的情况下对颜色进行聚类：

使用 "KMeans" 方法指定用作质心的初始颜色：

Create random 2D vectors:

Find different clusterings of data using the "KMeans" method by varying the "InitialCentroids":

可能存在的问题  (1)

创建和可视化嘈杂的二维月亮形状训练和测试数据集：

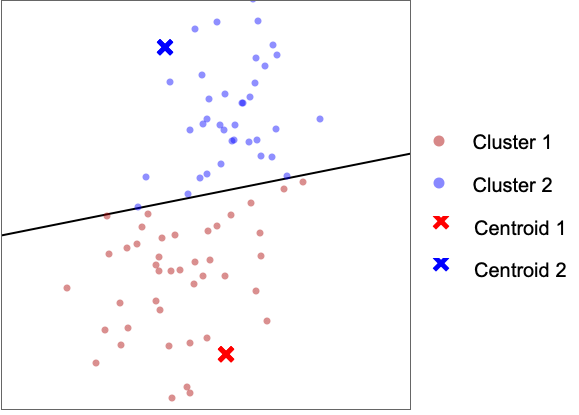
使用 "KMeans" 为两个聚类训练 ClassifierFunction 并在测试集中找到聚类：

可视化聚类表明 "KMeans" 在相互交织的聚类上表现不佳：