"Spectral" (Machine Learning Method)

Details & Suboptions

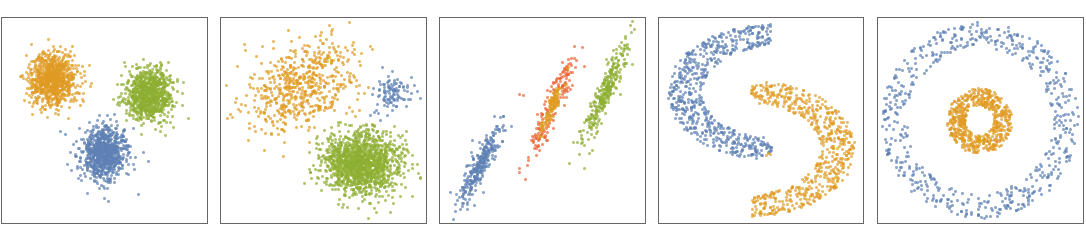
  • "Spectral" is a hybrid neighbor-based/centroid-based clustering method. "Spectral" works for arbitrary cluster shapes but requires clusters to have similar sizes. Since the method solves an eigenvalue problem, it is computationally expensive for large datasets.
  • The following plots show the results of the "Spectral" method applied to toy datasets:
  • To identify k clusters, the "Spectral" method uses the "KMeans" algorithm after reducing the data to k-dimensions. The dimensionality reduction is a neighbor-based nonlinear method similar to "Isomap": The adjacency matrix, A_(ij)=Exp[-d^2_(ij)/2sigma^2] is computed for every data point i, j. 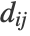is the distance between the points, and is a scale parameter. is then centered, normalized and linearly reduced to dimension k. Mathematically speaking, the centered and renormalized adjacency matrix is given by 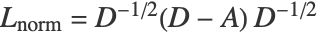, where is the diagonal matrix defined as 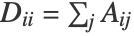. The largest k eigenvectors of constitute the reduced data.
  • The option DistanceFunction can be used to define .
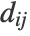  • The following suboption can be given:
  • "NeighborhoodRadius" Automaticvalue for scale parameter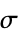

Examples

open allclose all

Basic Examples  (3)

Find clusters of numbers using the "Spectral" method:

Find up to four clusters using the "Spectral" method:

Train the ClassifierFunction on a list of colors using the "Spectral" method:

Gather the elements by their class number:

Create and visualize noisy 2D moon-shaped training and test datasets:

Train a ClassifierFunction using the "Spectral" method; find and visualize clusters in the test set:

Scope  (2)

Perform cluster analysis of a computed tomography scan image using the "Spectral" method:

Create a ClassifierFunction from a list of images and classify examples using the "Spectral" method:

Find the cluster assignments and gather the elements by their corresponding clusters:

Options  (3)

DistanceFunction  (1)

Find two clusters in data using Manhattan distance:

Define a set of two-dimensional data points, characterized by four somewhat nebulous clusters:

Plot clusters in data using Manhattan distance:

"NeighborhoodRadius"  (2)

Find clusters by specifying the "NeighborhoodRadius" suboption:

Generate two moon-shaped datasets and visualize them:

Plot different clusterings of data using the "Spectral" method by varying the "NeighborhoodRadius":