"Spectral" (Machine Learning Method)
- Method for FindClusters, ClusterClassify and ClusteringComponents.
- Partitions data into clusters of similar elements using a "Spectral" method.
Details & Suboptions
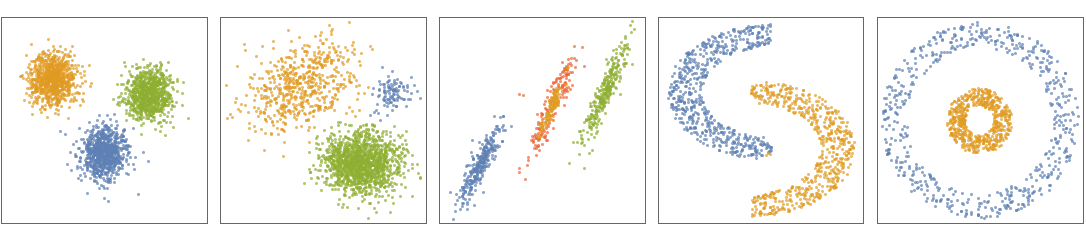
- "Spectral" is a hybrid neighbor-based/centroid-based clustering method. "Spectral" works for arbitrary cluster shapes but requires clusters to have similar sizes. Since the method solves an eigenvalue problem, it is computationally expensive for large datasets.
- The following plots show the results of the "Spectral" method applied to toy datasets:
- To identify k clusters, the "Spectral" method uses the "KMeans" algorithm after reducing the data to k-dimensions. The dimensionality reduction is a neighbor-based nonlinear method similar to "Isomap": The adjacency matrix,
![A_(ij)=Exp[-d^2_(ij)/2sigma^2] A_(ij)=Exp[-d^2_(ij)/2sigma^2]](Files/Spectral.en/2.png) is computed for every data point i, j.
is computed for every data point i, j. 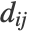 is the distance between the points, and
is the distance between the points, and  is a scale parameter.
is a scale parameter. 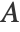 is then centered, normalized and linearly reduced to dimension k. Mathematically speaking, the centered and renormalized adjacency matrix is given by
is then centered, normalized and linearly reduced to dimension k. Mathematically speaking, the centered and renormalized adjacency matrix is given by 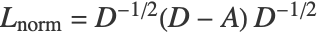 , where
, where  is the diagonal matrix defined as
is the diagonal matrix defined as 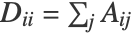 . The largest k eigenvectors of
. The largest k eigenvectors of  constitute the reduced data.
constitute the reduced data. - The option DistanceFunction can be used to define
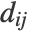 .
. - The following suboption can be given:
-
"NeighborhoodRadius" Automatic value for scale parameter 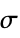
Examples
open all close allBasic Examples (3)
Find clusters of numbers using the "Spectral" method:
Find up to four clusters using the "Spectral" method:
Train the ClassifierFunction on a list of colors using the "Spectral" method:
Gather the elements by their class number:
Create and visualize noisy 2D moon-shaped training and test datasets:
Train a ClassifierFunction using the "Spectral" method; find and visualize clusters in the test set:
Scope (2)
Perform cluster analysis of a computed tomography scan image using the "Spectral" method:
Create a ClassifierFunction from a list of images and classify examples using the "Spectral" method:
Find the cluster assignments and gather the elements by their corresponding clusters: