"Spectral" （机器学习方法）

详细信息和子选项

  • "Spectral" 是一种混合的基于邻居/基于质心的聚类方法. "Spectral" 适用于任意簇形状，但要求簇具有相似的大小. 由于该方法解决的是特征值问题，因此对于大型数据集来说计算量很大.
  • 下图显示了应用于玩具数据集的 "Spectral" 方法的结果：
  • 为了识别 k 个簇，"Spectral" 方法在将数据降至 k-维后使用 "KMeans" 算法. 降维是一种基于邻居的非线性方法，类似于"Isomap"：邻接矩阵，A_(ij)=Exp[-d^2_(ij)/2sigma^2] 对每个数据点 i, j 进行计算. 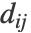是点之间的距离， 是尺度参数. 然后 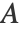居中、归一化并线性降到维度 k. 从数学上讲，居中和重新归一化的邻接矩阵由 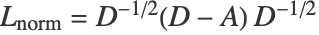给出，其中 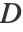是定义为 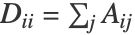的对角矩阵. 的最大 k 个特征向量构成降维后的数据.
  • 可以使用选项 DistanceFunction 定义 .
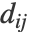  • 可以给出以下子选项：
  • "NeighborhoodRadius" Automatic尺度参数值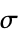

范例

打开所有单元关闭所有单元

基本范例  (3)

使用 "Spectral" 方法查找数字簇：

使用 "Spectral" 方法查找最多四个簇：

使用 "Spectral" 方法在颜色列表上训练 ClassifierFunction：

按类别号收集元素：

创建和可视化嘈杂的二维月亮形训练和测试数据集：

使用 "Spectral" 方法训练 ClassifierFunction；在测试集中查找和可视化集群：

范围  (2)

使用 "Spectral" 方法对 CT 扫描图像进行聚类分析：

从图像列表创建一个 ClassifierFunction 并使用 "Spectral" 方法对示例进行分类：

查找簇分配并按其相应的簇收集图像：

选项  (3)

DistanceFunction  (1)

使用曼哈顿距离查找 data 中的两个簇：

定义一组二维数据点，以四个有点模糊的簇为特征：

使用曼哈顿距离绘制 data 中的簇：

"NeighborhoodRadius"  (2)

通过指定 "NeighborhoodRadius" 子选项查找簇：

生成两个月亮形状的数据集并将其可视化：

通过改变 "NeighborhoodRadius" 使用 "Spectral" 方法绘制不同的 data 聚类：