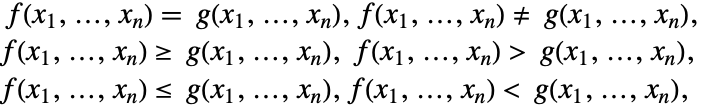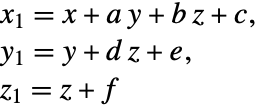はじめに

ディオファントス多項式系とは，整方程式および不等式で構築された式

を，下のように論理結合子と量限定子を使って結合したものである．

ここで，変数は整数値を表す．

変数 が あるいは の中に現れることを束縛出現， がその他の部分に現れることを自由出現という．系に変数 の自由出現がある場合， はその系の自由変数という．ディオファントス多項式系に量限定子が含まれない場合は，quantifier-freeという．決定問題とは，すべての変数が存在量化された系である．つまり，以下の形式の系のことである．

ここで はすべての変数となっている．決定問題(1)は，quantifier-freeの整方程式および不等式の系が整数解を持つかどうかによって，TrueとFalseのいずれかと等価になる．

以下は，ディオファントス多項式系の例である．

1742年に公式化されて未だに証明されていないゴールドバッハの予想(Goldbach's conjecture)[1]によると，系(2)はTrueと等価である．これは，Wolfram言語では任意のディオファントス多項式系が解けない可能性があることを示唆している．事実，ヒルベルト(Hilbert)の第10問題に対するMatiyasevichの解答[2]は，任意のディオファントス多項式系を解くアルゴリズムだけでなく，quantifier-freeの系や決定問題すら構築できないことを示している．それでもWolfram言語関数のReduce，Resolve，FindInstanceはかなり大きいクラスのディオファントス系をいくつか解くことができる．このドキュメントはこれらのクラスと，それを解くのにWolfram言語で使用されるメソッドについて説明する．メソッドは使用される順に提示する．

線形系

線形方程式系

連言の線形ディオファントス方程式は，任意数の変数について解くことができる．Wolfram言語では，Wolfram言語でHermiteDecompositionとして直接利用できる，行列のエルミート標準形の計算に基づくメソッドが使われる．その結果には，無制約の新しい整数パラメータが含まれる可能性がある．方程式が独立ならば，パラメータの数は変数の数と方程式の数との差に等しい．

フロベニウス(Frobenius)方程式

フロベニウス方程式は，以下の形式

を持つ方程式である．ここで， は正の整数， は整数であり，解の座標 は非負の整数でなければならない．

フロベニウス方程式の解のインスタンスを求める場合，Wolfram言語はフロベニウスグラフ[11]のcritical treeの計算に基づく高速アルゴリズムを使用する． の中の最小のものがMaxFrobeniusGraphシステムオプションの値（デフォルトは100万）を超えない場合に，このアルゴリズムが適用される．それ以外の場合は，より一般的な境界のある線形系の解法が使われる．関数FrobeniusSolveおよびFrobeniusNumberは，フロベニウス方程式を解いたり，フロベニウス数を計算したりするための特化された機能を提供する．

有界の線形方程式および不等式の系

線形方程式および不等式の系の実数解集合が有界の多面体である場合，系には有限多数の整数解が存在する．この解を求めるために，Wolfram言語は次の手順を踏む．

まず，この系は という形式を取るものとする．ここで は の整数行列，は長さ の整数ベクトル，は の整数行列，は長さ の整数ベクトルである．最初に が成り立つような整数ベクトル と，行が の零空間を生成するような の整数行列 N を見付けるために，線形方程式系の解法が使われる．の整数解集合はに等しい． であり であるとする．の整数解集合はに等しい．ここで は の整数解集合である．集合 をより効率よく見付けるために，Wolfram言語はLatticeReduceを使って を簡約し を得る．ただし， の列が線形依存ならば， には解がない（あるいは無限多数の解があるが，これでは仮定に反する）．は線形非依存の列を持つと仮定できるので， は 列持つ．とする．格子 の小さいベクトル を見付けるためには，格子基底還元法を使うこともできる．が を成り立たせるようにする．集合 は式 を使って，となるようなすべての の集合 から計算することができる．

集合 を見付けるためには，単純な再帰法を使うことができる．このアルゴリズムはLinearProgrammingを使って最初の変数の境界を見付け，その上・下限間のそれぞれの整数値 について，最初の変数を に設定して再帰的に自身を呼び出す．このアルゴリズムはシステムオプションのBranchLinearDiophantineがFalseに設定されているときに使われる．デフォルト設定のTrueでは，再帰法と分枝限定法とを組み合せたハイブリッドのアルゴリズムが使われる．再帰の各レベルで，最初の変数（単位立方とともに設定される実数解に含まれる点集合の投影として定義される）の「中間」値に対して再帰が継続される．一方，分枝限定法を使って，整数解を求めて実数解の残りの部分が検索される．FindInstanceは分枝限定法を使って，必要な の単独要素を見付ける．

BranchLinearDiophantineとLatticeReduceDiophantineの2つのシステムオプションを使うと，使用される厳密なアルゴリズムを制御することができる．これらのオプションの値を変更することで，Reduceのパフォーマンスが著しく向上する場合もある．

Wolfram言語は，系の整数解の数がシステムオプションDiscreteSolutionBoundの値の 次ベキ（ は方程式の解格子の次元）の最大値，およびシステムオプションExhaustiveSearchMaxPointsの値の第2要素を超えていない場合のみ，解を明示的に列挙する．

変数が2つあり，方程式がないので，解の数の上限はになる．Reduceは解を明示的に列挙することができる：

線形方程式および不等式の任意の系

quantifier-freeの線形ディオファントス方程式および不等式の系は，任意数の変数について解くことができる．この系は，選言標準形，つまり連言の選言として書かれ，各連言は別々に解かれる．連言に方程式しか含まれていない場合，線形方程式の解法が使われる．変数の数と方程式の数との違いが1以下である場合，Wolfram言語は線形方程式の解法を使って方程式を解き，解に多くて1つの自由パラメータが含まれる場合（一般に真である）は解を不等式に代入して，パラメータに対する不等式制約を決定する．この他のquantifier-freeの線形ディオファントス方程式および不等式の系には，Wolfram言語では[3]で記述されているアルゴリズムに束縛変数を扱うための線形計画法に基づく向上が加わったものが使われる．結果には非負の新しい整数パラメータが含まれ，新パラメータの数は変数の数を超える可能性がある．

一元系

一元方程式

一元方程式の整数解を見付けるために，Wolfram言語では[5]で記述された向上を含む[4]で与えられたアルゴリズムの変形が使われる．このアルゴリズムを使うと，実数根の分離法で扱えるよりもずっと高次で，整数の因数分解法で扱えるよりも格段に大きい自由項を持つ多項式の整数解を求めることができる．

一元方程式および不等式の系

一元ディオファントス方程式および不等式の系は，選言標準形で書かれ，各連言は別々に解かれる．連言に方程式が含まれる場合は，一元方程式の解法が使われ，残りの方程式および不等式を満足する解が選ばれる．

ここでReduceは の整数解を求め，不等式 を満足する解を選ぶ：

不等式だけを含む連言は，実数上で解かれる．結果の実数区間の整数解は，与えられた区間の数がシステムオプションDiscreteSolutionBoundの値を超えない場合に明示的に与えられる．このオプションのデフォルト値は10である．これより多い整数解を含む区間では，解は暗示的に表される．

多元系

二次方程式

Wolfram言語は任意の二元二次ディオファントス方程式を解くことができる．この方程式の一般形は以下の通りである．

が成り立ち，とが線形多項式であるなら，方程式(1)はと等価であり，線形ディオファントス方程式を解くメソッドが使われる．既約多項式では，使われるアルゴリズムおよび結果の形式は，二次形式の行列式に依存する．このアルゴリズムでは整数の因数分解が使われるため，結果の正確さはPrimeQで使用される確率的素数判定法の正確さに依存する．

でありが整数ならば，が成り立つ．ここでおよびは線形多項式であり， が成り立つ．この場合，方程式(1)は のすべての除数 について線形系の選言 と等価である．それぞれの線形系は有理数上に1つの解を持つため，方程式(1)には有限数の整数解が存在する．

以下は，の二元二次方程式である：

であり，が整数でないならば，方程式(1)はペル(Pell)タイプの方程式である．このような方程式の解法は18世紀から開発されており，[6]および[7]（しかし，両者ともアルゴリズムの完全な記述は含んでいない）に基づいて構築することができる．解の集合は，指数に表れる整数パラメータによってパラメータ化された空集合あるいは無限集合である．

ペル方程式は という形式の方程式であり，このとき は正方行列ではない．小さい係数を持つペル方程式では，解が非常に複雑になることがある：

A Pell equation is an equation of the form , where is not a square. Solutions to Pell equations with small coefficients can be quite complicated.

のときのペル方程式の解である：

のとき，，， であるとする．なので，，は非零の整数であり，である．よって，以下のようになる．

， とすると，方程式(1)は以下と等価になる．

ここで と仮定する．方程式(1)が整数解を持つなら，は の整数解を持つことになるため，は2つの線形多項式の積となる．ここではは既約なので，方程式(1)には整数解がない．

ならば，方程式(2)は以下を意味する．

モジュラ方程式(3)に の解がない場合，方程式(1)には整数解がない．（ならば，モジュラ方程式(3)には という解が1つある．そうでない場合，モジュラ方程式(3)のの解について， となるものもある．方程式(2)で という置換を行い， についての結果の線形方程式を解くと，以下が得られる．

はモジュラ方程式(3)を満足するので，(4)の最終項での除算の結果は整数となる． であり， なので，となる．方程式(4)および ということを考えると，以下が得られる．

従って，放物型方程式(1)の完全な解は， が整数となるようなモジュラ方程式(3)のそれぞれの解 に対して，方程式(4)および(5)で与えられる解の1パラメータ族で構成される．

であれば，方程式(1)の解は楕円上の整数点である．楕円は閉集合なので，解の数は有限となる．整数点を見付ける明らかなアルゴリズムは， が取り得る整数値の有限数のそれぞれについて， の解を計算することである．しかし，この計算は大きい楕円では極めて遅い．Wolfram言語では[8]に記述されているこれより速いアルゴリズムを使う．

以下でReduceは楕円型二次方程式の正の整数解を求める． の取り得る正の整数値は個より多いので，この楕円には明確なアルゴリズムは役に立たない：

Thue方程式

Thue方程式は，

という形式のディオファントス方程式である．ここでは次数の既約同次形式である．

Thue方程式の解の数は常に有限である．Wolfram言語では，解を見つけるのに必要な時間が，次数および係数の大きさに従って飛躍的に長くなるが，実質的に任意のThue方程式が解ける．アルゴリズムの最も難しい点は，解の大きさについての限界を計算することである．Wolfram言語ではBaker-Wustholzの定理に基づくアルゴリズムを使って，限界[9]を求める．解について妥当な大きさの限界を与える不等式が入力に含まれている場合は，Wolfram言語はもっと速く解が計算できる．

ここでReduceは，最大100桁の 座標を持つ15次Thue方程式の一意解を見付ける．解の大きさの限界がなかったら，Reduceは1000秒以内では計算を終了できない：

多元非線形系

モジュラふるい法で解ける系

Wolfram言語では，モジュラふるい法の変形（例として[9]を参照）が使われる．このメソッドは，「系に整数 を法とする整数の解がないことにより，系が整数解を持たない」ということを証明する．それ以外の場合は，小さい整数座標の解を見付けるか，系には と の間のすべての座標で整数解がないことを証明する．ふるい法が検定することのできる解の点の候補数は，システムオプションSieveMaxPointsで制御される．

複数の方程式を含む系

ディオファントス多項式系に，複数の方程式が含まれている場合，Wolfram言語ではGroebnerBasisを使って問題を簡単な問題の列に還元することが試みられる．

Wolfram言語は初期変数の最小数に依存するグレブナー基底の要素を解くことを試みる．解の数が有限ならば，Wolfram言語はそれぞれの解について計算された値を代入し，得られた系を残りの変数について解くことを試みる．

以下の最初の方程式には および について4つの整数解がある．このそれぞれの解に対して，2つ目の方程式は の1元方程式となる．4つの1変量方程式には，合計で2つの整数解がある：

ここでは最初の方程式は1つの解を持つThue方程式である． と に最初の方程式で計算された値を代入すると，2番目の方程式はペル方程式になる：

このヒューリスティックは

という形式のグレブナー基底を持つ系に適用される．この場合，Wolfram言語は以下の合同式系を解く．

その解は，新しい整数パラメータを使って表される．これらは，もとの系に存在する方程式 および不等式に代入される．Wolfram言語は，それで得られた系を新しいパラメータについて解くことを試みる．

二乗和

Wolfram言語では，[10]に記述されているアルゴリズムを使って以下の形式の方程式を解くことができる．

Wolfram言語は多元二次方程式の場合，方程式を(2)の形式に変形するアフィン変換を探す．これにはCholeskyDecompositionに基づくヒューリスティック法が使われる．しかし，(2)の形式で表現できる方程式では，このメソッドが失敗することがある．

(2)の単独解を見付けるために，FindInstanceは[12]に基づくアルゴリズムを使う．

ピタゴラス方程式

Wolfram言語はピタゴラス方程式の解が分かる．

3変数の二次方程式の場合，Wolfram言語は方程式をピタゴラス方程式に変換して，以下の形式

の変換を見付けようとする．

可約な非定数部を持つ方程式

1つの方程式の非定数項の和が因数分解されるとき，Wolfram言語は以下の公式

を使って，その方程式を1対の低次の方程式からなる選言に簡約する．この簡約は， の約数がすべて見付けられるかどうかに依存するので，結果の正確さはPrimeQで使用される確率的素数判定法の正確さに依存する．

一次変数を持つ方程式

Wolfram言語は，

の形式のディオファントス系（ここでは不等式の連言あるいはTrue）を解こうとするとき，その系を

に簡約する．系(3)の最初の部分は，複数の方程式を含む系の解法を使って解く．Wolfram言語は，系(3)の2番目の部分が解ける3つの場合を認識する．であれば，解は で与えられ，不等式を解くことで得られる の制約でも与えられる．不等式の非線形系は，CylindricalDecompositionを使って解かれる．整数定数が のとき であれば，系(3)の2番目の部分の解は により与えられ，また合同式 を解いた後，その合同式の解のそれぞれについて不等式を解くことにより得られる の制約でも与えられる．が非定数であるとき，Wolfram言語は であれば系(3)の2番目の部分が解ける．Wolfram言語は前処理段階ですべての方程式を因数分解するので，と は互いに疎であると仮定できる．従って，整数 ，整数係数を持ちである多項式 および について，以下が成り立つ．

が整数ならば，は整数であり，，も整数である．なので，最後の条件は整数 の有限数だけが満足する．ゆえに，系(3)の2番目の部分の解は，解の候補の有限数から選ぶことができる．

また，Wolfram言語では系(3)が解を持たない場合を検出するのに以下のヒューリスティックが使われる．が常に で割り切れ，は決して では割り切れないような整数 がある場合，系(3)には解がない． の候補は，いくつかの点で の値のGCDを計算することで見付かる．

最後の2つのメソッドは，点の有限集合上でしらみつぶし法を使う．使用できる探索点の数は，システムオプションであるSieveMaxPointsで制御される．

以下は で(3)に還元される：

以下は で(3)に還元される：

以下は の系(3)に還元される：

は常に5で割り切れるが，は決して5では割り切れないため，ここでReduceは方程式に解がないことを突き止める：

空あるいは有限の実数解集合を持つ系

ディオファントス多項式系が他の方法で解かれない場合，Wolfram言語はCAD (Cylindrical Algebraic Decomposition)法を使って実数上で系を解く．系に実数解がない場合は，明らかに整数解はない．実数解の集合が有限ならば，整数解の数は有限である．この場合原則として，すべての整数解は円筒分解から見付けることができる．すなわち，各円筒について，第1座標で取り得る整数値をすべて列挙し，第1座標の各値に対して，第2座標で取り得る整数値すべてを列挙していくというふうにするのである．しかし，大きな有限の解集合では，この方法を使うと，かなり多数の点を試みなければならなくなる可能性がある．従って，Wolfram言語には実数区間で明示的に列挙される整数解の数に制限がある．実数解集合が無限である系，あるいは有限であっても大きいという系では，解はCADおよびすべての変数は整数であるという条件を返すことにより，暗示的に表される．多元系では，そのような暗示的な表現では整数解が存在するかどうかを判断するのに十分ではないことがある．このことは，ヒルベルトの第10問題に対するMatiyasevichの解[2]を考えると，明白である．

ここでモジュラふるい法によりに解がないことが分かる．この立方を除去するために不等式を加えると，Reduceには，この方程式にはどこにも解がないということが分かる：

形式 の方程式

Wolfram言語では，

という形式のディオファントス方程式（ここでは不等式の連言かTrue）を

に変換することにより解こうとする．結果の系(4)は，解きやすくなっていることも，そうでないこともある．この変換を任意回数だけ再帰的に適用できる系が存在するため，Wolfram言語ではヒューリスティックが確実に終了するようにするために，反復限度が使われる．

しらみつぶし探索で解ける系

すべての変数について上限と下限を明示的に含んでいる系では，Wolfram言語は解を求めるためにしらみつぶし探索を使う．検索の範囲はシステムオプションExhaustiveSearchMaxPointsの値で指定される．このオプション値は整数のペア（デフォルトはである）でなければならない．範囲内の整数点の数が最初の整数を超えない場合は，1元多項式の解法以外の解法の代りにしらみつぶし探索が使われる．範囲内の整数点の数が2つ目の整数を超えない場合は，すべての方法が失敗した後でしらみつぶし探索法が使われる．

オプション

ディオファントス多項式系を解くWolfram言語関数には，操作方法を制御するオプションが数多く備わっている．このセクションでは，そのようなオプションを要約する．

ディオファントス多項式系の動作に影響を与えるReduceのオプション

GeneratedParameters

Reduceでディオファントス系の無限解を表すためには，新しい整数パラメータを導入する必要がある．新しいパラメータの名前は，オプションGeneratedParametersで指定される．GeneratedParameters->f とすると，新しいパラメータの名前はf[1], f[2], …となる．

ReduceOptionsグループのシステムオプション

ここで挙げるのは，ディオファントス多項式系でのReduce，Resolve，FindInstanceの動作に影響を及ぼすReduceOptionsグループのシステムオプションである．これらのオプションは以下のように設定する．

SetSystemOptions["ReduceOptions"->{"option name"->value}]

ディオファントス多項式系でReduce，Resolve, FindInstanceの動作に影響を及ぼすReduceOptionsグループオプション

システムオプションBranchLinearDiophantineの値は，有界の線形系を解く最終段階でアルゴリズムのどの変形を使うかを指定する．デフォルト設定の"BranchLinearDiophantine"->Falseでは，単純な再帰列挙法が使われる．"BranchLinearDiophantine"->Trueの場合は，Reduceは分枝限定法と単純な再帰的列挙法を組み合せたハイブリッドのメソッドを使う．

次は により制限されたシンプレックス内の7つの変数による，ランダムに生成された2つの方程式 とランダムに生成された3つの不等式 から成る系を解く．ここでは，アルゴリズムによる速度の違いは上より小さい：

システムオプションDiscreteSolutionBoundの値は，実数区間 の整数解を明示的に列挙するか， として暗示的に表現するかを指定する．DiscreteSolutionBound->n と設定すると，与えられた実数区間の整数解は，その数が n を超えない限り明示的に列挙される．このオプションのデフォルト値は10である．

実数区間には10個の整数がある．Reduceにより，それが明示的に書き出される：

実数区間には11個の整数がある．Reduceにより，それが暗示的に表現される：

DiscreteSolutionBoundの値は，有界線形系および有限個の解を持つ他のディオファントス系の解法にも影響を与える．有界の領域で多数の解を明示的に列挙する必要がある場合，DiscreteSolutionBoundをInfinityに設定する．

システムオプションExhaustiveSearchMaxPointsはしらみつぶし探索法によって使用される探索点の最大数を指定する．オプション値は整数のペア（デフォルトは）でなければならない．範囲内の整数点の数が最初の整数を超えないならば，1元多項式の解法以外の解法の代りにしらみつぶし探索法が使われる．範囲内の整数点の数が2つ目の整数を超えなければ，すべてのメソッドが失敗した後でしらみつぶし探索法が使われる．

ExhaustiveSearchMaxPoints の第2要素の値をに増やす：

ExhaustiveSearchMaxPointsの最初の要素をに増やすと，Reduceは最初にしらみつぶし探索法を使う．この例では，ペル方程式のソルバよりも探索がずっと遅い：

システムオプションDiscreteSolutionBoundは実数区間 の整数解を明示的に列挙するか， として暗示的に表すかを指定する．DiscreteSolutionBound->n の場合，与えられた実数区間の整数解の数が n を超えなければその整数解は明示的に列挙される．このオプションのデフォルト値は10である．

システムオプションLatticeReduceDiophantineの値は，有界の線形不等式系の前処理にLatticeReduceを使うかどうかを指定する．LatticeReduceの使用は，軸上に投影するよりも非軸線上に投影した方がずっと小さくなる多面体を記述する不等式系にとって重要である．しかし，LatticeReduceにより問題が簡約される代りに格段に難しくなってしまう系もある．

両軸に投影すると より大きいが，線 に投影すると大きさが1になるような三角形の中には，2つの整数点しか見付からない：

非デフォルトのメソッドはこの系ではかなり遅い．速度差は に比例する：

これは簡単な不等式 の集合を含む系である．これは比較的複雑な不等式 と合せて，解を適度に小さい大きさの多面体に制限する．この系ではLatticeReduceを使った方が速い：

システムオプションMaxFrobeniusGraphは，FindInstanceがフロベニウスグラフ[11]のcritical treeの計算に基づいたアルゴリズムを使用する対象であるフロベニウス方程式の最小定数の最大の大きさを指定する．それ以外の場合は，より一般的な有界の線形系を解くメソッドが使われる．有界の線形系を説く一般的なメソッドとは異なり，フロベニウスグラフの計算に基づく方法は変数の数にほとんど依存しないので，多数の変数がある方程式ではこの方が速い．もう一方で，このメソッドは最小の係数の大きさのグラフを保存することが必要なので，大きい係数の場合は，メモリが足りなくなる可能性がある．

より大きい最小の係数を持つフロベニウス方程式を解くために，FindInstanceはデフォルトで有界の線形系を解く一般的なメソッドを使う．この例では，メソッドは比較的遅いがほとんどメモリを使わない．現行の例で使用されるメモリを表示するために，カーネルが再起動されている：

MaxFrobeniusGraphの値をに増やす：

システムオプションSieveMaxPointsは，モジュラふるい法により使用される検索点，および線形変数を持つ方程式の解法で使用される検索により使われる検索点の最大数を指定する．オプションの値はというペアである．より遅い解法の前に， 個の点までの検索が試される．決定問題の場合，すべてのメソッドが失敗した後， 個までの点を含む別の短k策法が試される．このオプションのデフォルト値はである．　

SieveMaxPointsの第2要素をに増やすと，FindInstanceで問題が解けるようになる：

SieveMaxPointsの第1要素をに増やすと，Reduceで完全に問題が解ける：

参考文献

[8] Hardy, K., J. B. Muskat and K. S. Williams. "A Deterministic Algorithm for Solving in Coprime Integers and ." Mathematics of Computation 55 (1990): 327–343.