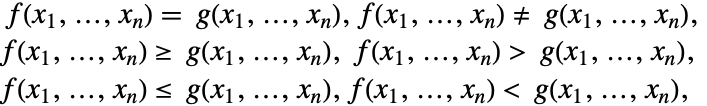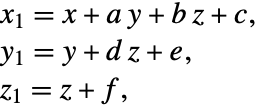丢番图多项式系统
介绍
在 ![]() 或
或 ![]() 内部出现变量
内部出现变量 ![]() , 称为约束出现,任何其它情况下
, 称为约束出现,任何其它情况下 ![]() 的出现都称为一个自由出现. 如果多项式系统含有变量
的出现都称为一个自由出现. 如果多项式系统含有变量 ![]() 的一个自由出现,则变量
的一个自由出现,则变量 ![]() 被称作该系统的自由变量. 如果一个丢番图多项式系统不含量词,则该系统为无量词系统. 决策问题是全部变量被存在性量化(existentially quantified)的系统,即一个形如
被称作该系统的自由变量. 如果一个丢番图多项式系统不含量词,则该系统为无量词系统. 决策问题是全部变量被存在性量化(existentially quantified)的系统,即一个形如
的系统,其中 ![]() 代表
代表 ![]() 中的所有变量. 决策问题(1)等价于 True 或 False,取决于多项式方程和不等式
中的所有变量. 决策问题(1)等价于 True 或 False,取决于多项式方程和不等式 ![]() 的无量词系统是否有整数解.
的无量词系统是否有整数解.
于1742年提出、至今仍未证实的歌德巴赫猜想 [1] 断言系统(2)等价于 True. 这表明 Wolfram 语言可能不能求解任意丢番图多项式系统. 事实上,马季亚谢维奇(Matiyasevich)关于希尔伯特第十问题的解 [2] 表明,不存在任何解法能够求解任意丢番图多项式系统,甚至对无量词系统或是决策问题也是如此. 尽管如此,Wolfram 语言函数 Reduce、Resolve 和 FindInstance 还是能够对丢番图系统中几个相当大的类别求解. 本教程将解释这些系统类别以及 Wolfram 语言对这些类别求解的方法. 这些方法按照被使用的次序来分别介绍. 本教程也将介绍影响这些方法的选项以及它们的作用.
线性系统
线性方程系统
线性丢番图方程组的合取(Conjunctions of linear Diophantine equations)对于任意数目的变量可解. Wolfram 语言使用一种基于计算厄米正交矩阵的方法,这种方法在 Wolfram 语言中通过 HermiteDecomposition 可直接使用. 结果可能含有新的不受限制的整数参数. 如果方程互相独立,参数个数等于变量个数与方程个数之差.
Frobenius 方程
的方程,其中 ![]() 为正整数,
为正整数,![]() 为整数,解的坐标
为整数,解的坐标 ![]() 要求是非负整数.
要求是非负整数.
为了找到Frobenius 方程解的实例,Wolfram 语言使用的是一种基于 Frobenius 图中计算临界树 [11] 的快速算法. 该算法适用于 ![]() 中的最小值不超过 MaxFrobeniusGraph 系统选项值(默认值为1,000,000)的情形. 其它时候将使用一种更一般的用于求解有界线性系统的方法. 函数 FrobeniusSolve 与 FrobeniusNumber 为求解 Frobenius 方程和计算 Frobenius 数提供了专业化的功能.
中的最小值不超过 MaxFrobeniusGraph 系统选项值(默认值为1,000,000)的情形. 其它时候将使用一种更一般的用于求解有界线性系统的方法. 函数 FrobeniusSolve 与 FrobeniusNumber 为求解 Frobenius 方程和计算 Frobenius 数提供了专业化的功能.
有界线性方程和不等式系统
如果线性方程和不等式系统的一个实数解集是一个有界的多面体,则系统存在有限多的整数解. 为了找到这些解, Wolfram 语言使用下述步骤.
用户可以假设系统有这种形式: ![]() ,其中
,其中 ![]() 为一个
为一个 ![]() 整数矩阵,
整数矩阵,![]() 为一个长度为
为一个长度为 ![]() 的整数向量,
的整数向量,![]() 为一个
为一个 ![]() 整数矩阵,以及
整数矩阵,以及 ![]() 为一个长度为
为一个长度为 ![]() 的整数向量. 首先,使用求解线性方程系统的方法找到一个整数向量
的整数向量. 首先,使用求解线性方程系统的方法找到一个整数向量 ![]() ,使得
,使得 ![]() 以及一个
以及一个 ![]() 的整数矩阵 N,其各行生成
的整数矩阵 N,其各行生成 ![]() 的零空间.
的零空间. ![]() 的整数解集等于
的整数解集等于 ![]() . 令
. 令 ![]() ,
,![]() .
. ![]() 的整数解集等于
的整数解集等于 ![]() ,其中
,其中 ![]() 为
为 ![]() 的整数解集. 为提高找到集合
的整数解集. 为提高找到集合 ![]() 的效率,Wolfram 语言使用 LatticeReduce 简化
的效率,Wolfram 语言使用 LatticeReduce 简化 ![]() ,得到
,得到 ![]() . 注意到若
. 注意到若 ![]() 的各列线性相关,则
的各列线性相关,则 ![]() 无解(否则会有无穷多的解,这与假设矛盾). 因此可以假设
无解(否则会有无穷多的解,这与假设矛盾). 因此可以假设 ![]() 具有线性无关的列,因此
具有线性无关的列,因此 ![]() 有
有 ![]() 列. 令
列. 令 ![]() . 格规约法(Lattice reduction technique)也用于在格点(lattice)
. 格规约法(Lattice reduction technique)也用于在格点(lattice)![]() 中寻找小型向量
中寻找小型向量 ![]() . 令
. 令 ![]() 满足
满足 ![]() . 集合
. 集合 ![]() 可以由满足
可以由满足 ![]() 的所有的
的所有的![]() 的集合
的集合 ![]() ,根据公式
,根据公式 ![]() 计算得到.
计算得到.
为了得到集合 ![]() ,可以使用一种简单的递归算法. 该算法使用 LinearProgramming 得到第一个变量的边界,对于边界内部的每一个整数值
,可以使用一种简单的递归算法. 该算法使用 LinearProgramming 得到第一个变量的边界,对于边界内部的每一个整数值 ![]() ,将第一个变量设定为
,将第一个变量设定为 ![]() 递归地调用自身. 该算法是在系统选项 BranchLinearDiophantine 设为 False 时使用. 在默认设置 True 时,使用的是一种结合了递归算法和分支定界 (branch and bound) 算法的混合算法. 在递归的每一层,递归在第一个变量的中间值继续(定义为单位立方体内实数解集的点集的投影)而对于实数解集的剩余部分,则使用分支定界算法来寻找其中的整数解. FindInstance 使用分支定界算法得到它所需要的
递归地调用自身. 该算法是在系统选项 BranchLinearDiophantine 设为 False 时使用. 在默认设置 True 时,使用的是一种结合了递归算法和分支定界 (branch and bound) 算法的混合算法. 在递归的每一层,递归在第一个变量的中间值继续(定义为单位立方体内实数解集的点集的投影)而对于实数解集的剩余部分,则使用分支定界算法来寻找其中的整数解. FindInstance 使用分支定界算法得到它所需要的 ![]() 的单一元素.
的单一元素.
有两种系统选项,BranchLinearDiophantine 和 LatticeReduceDiophantine 允许用户对使用何种算法进行控制. 在某些情况下,改变这些选项的值可以显著改善 Reduce 的效果.
Wolfram 语言只有在系统整数解的个数不超过系统选项DiscreteSolutionBound 的值的 ![]() 次幂时才将解显式地列出,其中
次幂时才将解显式地列出,其中 ![]() 为方程组的解的格点(solution lattice)的维数,也是系统选项 ExhaustiveSearchMaxPoints 的值的第二个元素.
为方程组的解的格点(solution lattice)的维数,也是系统选项 ExhaustiveSearchMaxPoints 的值的第二个元素.
任意线性方程和不等式系统
线性丢番图方程和不等式的无量词系统对于任意数目的变量都是可解的. 该系统以析取范式(disjunctive normal form)也就是合取(conjunctions)的析取(disjunction)形式写出,并对每一个合取分别求解. 若一个合取只含有方程,则使用求解线性方程系统的方法. 若变量个数与方程个数之差最多为1,Wolfram 语言使用求解线性方程系统的方法来求解方程组,同时如果解中至多存在一个自由参数(一般情况如此),则将解代回到不等式中来决定参数的不等式限制条件. 对于线性丢番图方程和不等式的无量词系统的所有其它情形,Wolfram 语言采用 [3] 中介绍的算法,在处理有界变量上进行某些基于线性规划的改进. 结果中可能含有新的非负整数参数,且新参数的数目可能要大于变量的数目.
单变量系统
单变量方程
为得到单变量方程的解 Wolfram 语言使用的方法是基于 [4] 中给出的算法的一种变体、并进行了 [5] 中所介绍的改进. 应用该算法能够得到整数解的多项式的次数可以大大高于实根隔离算法所能求解的多项式的次数,并且其自由项也可以比整数分解算法能够处理的自由项大得多.
单变量方程和不等式系统
单变量丢番图方程和不等式系统以析取范式写出,并且每一个合取都单独求解. 如果一个合取包含一个方程,则使用求解单变量方程的方法,并选择满足其余方程和不等式的解.
只包含不等式的合取在整个实数域内求解. 如果结果实数区间上的整数解的数目不超过系统选项 DiscreteSolutionBound 的值,则这些整数解将被显式给出. 该选项的默认值为10. 对于区间上整数解的数目过大的情况,这些解将被隐式表示.
双变量系统
二次方程
Wolfram 语言能够对于含有双变量的任意二次丢番图方程求解. 这种方程的一般形式为
若 ![]() ,其中
,其中 ![]() 和
和 ![]() 为线性多项式,则方程(1)等价于
为线性多项式,则方程(1)等价于 ![]() ,求解线性丢番图方程的方法将被使用. 对于不可约多项式
,求解线性丢番图方程的方法将被使用. 对于不可约多项式 ![]() ,所用算法及结果的形式取决于二次形式的行列式
,所用算法及结果的形式取决于二次形式的行列式 ![]() . 该算法可能用到整数因式分解,因此结果的正确与否取决于 PrimeQ 所用的概率素性检验(probabilistic primality test)的正确性.
. 该算法可能用到整数因式分解,因此结果的正确与否取决于 PrimeQ 所用的概率素性检验(probabilistic primality test)的正确性.
带有平方行列式(Square Determinant)的双曲型方程(Hyperbolic-Type Equations)
若 ![]() 且
且 ![]() 为整数,则
为整数,则 ![]() ,其中
,其中![]() 和
和 ![]() 为线性多项式,且
为线性多项式,且 ![]() . 这种情况下,对于所有
. 这种情况下,对于所有 ![]() 的除数
的除数 ![]() ,方程(1)等价于线性系统
,方程(1)等价于线性系统 ![]() 的析取. 每一个线性系统在有理数域内有一个解,因此方程(1)的整数解个数有限.
的析取. 每一个线性系统在有理数域内有一个解,因此方程(1)的整数解个数有限.
带有非平方行列式(Nonsquare Determinant)的双曲型方程(Hyperbolic-Type Equations)
若 ![]() 且
且 ![]() 非整数,则方程(1)为 Pell 型方程. 求解这类方程的方法自18世纪起就已提出,可以在 [6] 和 [7] 的基础之上构建(尽管这些书并没有对该算法给出一个完整的介绍). 解集为空或者无穷,由出现在指数上的一个整数参数进行参数化.
非整数,则方程(1)为 Pell 型方程. 求解这类方程的方法自18世纪起就已提出,可以在 [6] 和 [7] 的基础之上构建(尽管这些书并没有对该算法给出一个完整的介绍). 解集为空或者无穷,由出现在指数上的一个整数参数进行参数化.
抛物型方程
如果 ![]() ,设
,设 ![]() ,
,![]() ,且
,且 ![]() . 由于
. 由于 ![]() ,所以
,所以 ![]() 和
和 ![]() 为非零整数,且
为非零整数,且 ![]() . 则有
. 则有
设 ![]() 且
且 ![]() . 则方程 (1) 等价于
. 则方程 (1) 等价于
假设 ![]() . 若方程 (1) 存在整数解,则可得出
. 若方程 (1) 存在整数解,则可得出 ![]() 对
对 ![]() 有整数解,于是
有整数解,于是 ![]() 为两个线性多项式的乘积. 由于此处
为两个线性多项式的乘积. 由于此处 ![]() 不可约,所以方程 (1) 无整数解.
不可约,所以方程 (1) 无整数解.
若 ![]() ,则方程 (2) 意味着
,则方程 (2) 意味着
若模方程 (3) 对 ![]() 无解,则方程 (1) 无整数解. (若
无解,则方程 (1) 无整数解. (若 ![]() ,则模方程 (3) 有一解,
,则模方程 (3) 有一解,![]() .)否则对于模方程 (3) 的某个解
.)否则对于模方程 (3) 的某个解 ![]() ,有
,有 ![]() . 在方程 (2) 中进行
. 在方程 (2) 中进行 ![]() 的替换,并对所得线性方程求关于
的替换,并对所得线性方程求关于 ![]() 的解得到
的解得到
注意到由于 ![]() 满足模方程 (3),(4) 中最后一项的相除给出一个整数结果. 由于
满足模方程 (3),(4) 中最后一项的相除给出一个整数结果. 由于 ![]() 且
且 ![]() ,所以
,所以![]() . 综合考虑方程 (4) 和
. 综合考虑方程 (4) 和 ![]() ,得到
,得到
因此,对于模方程 (3) 的每个解 ![]() ,抛物型方程 (1) 的全解由单参数的解族组成,由方程 (4) 和 (5) 给出,其中
,抛物型方程 (1) 的全解由单参数的解族组成,由方程 (4) 和 (5) 给出,其中 ![]() 是一个整数.
是一个整数.
椭圆型方程
若 ![]() ,方程 (1) 的解为一个椭圆上的整数点. 由于椭圆是一个有界集合,解集的个数一定是有限的. 找到整数点的一种显而易见的算法是对于有限的
,方程 (1) 的解为一个椭圆上的整数点. 由于椭圆是一个有界集合,解集的个数一定是有限的. 找到整数点的一种显而易见的算法是对于有限的 ![]() 的每一个可能整数值计算关于
的每一个可能整数值计算关于 ![]() 的解. 然而这种做法对于较大的椭圆可能会非常慢而不建议采用. Wolfram 语言使用的是 [8] 中介绍的一种较快的算法.
的解. 然而这种做法对于较大的椭圆可能会非常慢而不建议采用. Wolfram 语言使用的是 [8] 中介绍的一种较快的算法.
Thue 方程
Thue 方程的解的个数总是有限的. 原则上 Wolfram 语言能够解出任意 Thue 方程,尽管找到解所需的时间随着次数和系数大小的增加而迅速延长. 该算法最困难的部分是为解的尺寸计算出一个界限. Wolfram 语言使用一种基于 Baker–Wustholz定理的算法来找到这个界限 [9]. 如果在输入中含有对解提供适当界限的不等式,Wolfram 语言就可以更快地将解计算出来.
多变量非线性系统
可用模筛法(Modular Sieve Method)求解的系统
Wolfram 语言使用的是模筛法的一种变体 (参见 [9]). 该方法可以证明:由于系统按整数 ![]() 为模无解,则该系统无整数解. 否则,它可以找到一个小整数坐标的解,或是证明该系统在
为模无解,则该系统无整数解. 否则,它可以找到一个小整数坐标的解,或是证明该系统在 ![]() 和
和 ![]() 之间的全部坐标内无整数解. 允许筛法测试的候选解的点的个数由系统选项 SieveMaxPoints 控制.
之间的全部坐标内无整数解. 允许筛法测试的候选解的点的个数由系统选项 SieveMaxPoints 控制.
方程数大于一的系统
如果一个丢番图多项式系统的方程数大于一,Wolfram 语言使用 GroebnerBasis 来试图将问题约化为一系列较简单的问题.
通过在有限多部分解上迭代可解的系统
Wolfram 语言试图求解依赖于最小数目的初始变量的 Gröbner 基的一个元素. 如果解的个数是有限的,则对于每一个解,Wolfram 语言将计算得到的值代入系统,并在所得到的新系统中试图求解剩余的变量.
带有线性-三角形 Gröbner 基的系统
这种情况下,Wolfram 语言求解同余(congruences)系统
解由新的整数参数表示. 这些解被代入原始系统中的方程 ![]() 和不等式,然后 Wolfram 语言尝试对所得到的系统求解新的参数.
和不等式,然后 Wolfram 语言尝试对所得到的系统求解新的参数.
平方和
Wolfram 语言能够运用 [10] 中介绍的算法,求解形如
的方程. 对于多元二次方程,Wolfram 语言试图找到一个仿射变换(affine transformation)来将方程化为 (2) 的形式. 为达到这一目的,Wolfram 语言使用的是一种基于 CholeskyDecomposition 的试探法的方法. 然而对于一些可用形式 (2) 表示的方程,这种方法也可能会失败.
为了得到 (2) 的一个单一解,FindInstance 使用一种基于 [12] 的算法.
勾股方程(Pythagorean equation)
对于含有三个变量的二次方程,Mathematica 试图找到形如
带有可约化非常数部分的方程
如果一个方程的非常数项的和可因式分解,Wolfram 语言使用公式
将方程约化为次数较低的方程对的析取. 这种约化取决于找到 ![]() 的全部除数的能力,因此结果的正确与否取决于 PrimeQ 所用的概率素性检验(probabilistic primality test)的正确性.
的全部除数的能力,因此结果的正确与否取决于 PrimeQ 所用的概率素性检验(probabilistic primality test)的正确性.
带有一个线性变量的方程
的方法来求解,其中![]() 是不等式或 True 的合取.
是不等式或 True 的合取.
求解系统 (3) 的第一部分使用的是求解方程数大于一个的系统的方法. 当系统 (3) 的第二部分能够解出时,Wolfram 语言要识别三种情况. 若 ![]() ,解由
,解由 ![]() 和通过求解不等式
和通过求解不等式 ![]() 得到的对
得到的对 ![]() 的限制条件得到. 非线性不等式系统用 CylindricalDecomposition 来求解. 若对于一个整数常数
的限制条件得到. 非线性不等式系统用 CylindricalDecomposition 来求解. 若对于一个整数常数 ![]() ,
,![]() ,则系统 (3) 的第二部分由
,则系统 (3) 的第二部分由 ![]() 和通过求解同余
和通过求解同余 ![]() 、然后对于同余的每一个解求解不等式
、然后对于同余的每一个解求解不等式 ![]() 所得到的对
所得到的对 ![]() 的限制条件联立给出. 若
的限制条件联立给出. 若 ![]() 不是常数,在
不是常数,在 ![]() 时 Wolfram 语言可以求解系统 (3) 的第二部分. 由于 Wolfram 语言在预处理阶段将所有方程进行因式分解,
时 Wolfram 语言可以求解系统 (3) 的第二部分. 由于 Wolfram 语言在预处理阶段将所有方程进行因式分解,![]() 和
和 ![]() 可以被认为是互素的. 则有
可以被认为是互素的. 则有
其中 ![]() 为整数,多项式
为整数,多项式 ![]() 和
和 ![]() 的系数为整数,且
的系数为整数,且 ![]() . 若
. 若 ![]() 为整数,则
为整数,则 ![]() 为整数,由此得到
为整数,由此得到 ![]() 或
或 ![]() . 由于
. 由于 ![]() ,故只有有限个整数
,故只有有限个整数 ![]() 满足最后一个条件. 因此,系统 (3) 的第二部分的解能够从有限个候选解中选择.
满足最后一个条件. 因此,系统 (3) 的第二部分的解能够从有限个候选解中选择.
另外,Wolfram 语言使用下述试探法来识别系统 (3) 无解的情形. 如果存在一个整数 ![]() 使得
使得 ![]() 恒能被
恒能被 ![]() 整除,而
整除,而 ![]() 恒不被
恒不被 ![]() 整除,则系统 (3) 无解.
整除,则系统 (3) 无解. ![]() 的候选对象通过计算在一些点处
的候选对象通过计算在一些点处 ![]() 值的 GCD 得到.
值的 GCD 得到.
最后两种方法是在有限个点集上进行穷举搜索(exhaustive search). 所允许的搜索点的数目由系统选项 SieveMaxPoints 控制.
带有空集或有界实数解集的系统
如果一个丢番图多项式系统不能通过任何其它方法求解,Wolfram 语言将在实数上使用柱形代数分解 (CAD) 算法对系统求解. 如果系统无实数解,则很明显该系统无整数解. 如果实数解集有界,则整数解数目是有限的. 原则上讲,这种情形下所有的整数解都可以通过柱形分解找到. 也就是说,对于每一个柱形,对第一个坐标的所有可能整数值进行枚举,然后对于第一个坐标的每一个值,枚举第二个坐标的所有可能整数值,如此继续下去. 然而,对于大型有界解集,这种方法可能导致所试探的点的数目庞大. 鉴于此,Wolfram 语言有一个界限来在实数区间上对显式枚举整数解的数量加以限制. 对于实数解集无界或是界限巨大的系统,解是通过返回 CAD 和全体变量须为整数这样一个条件来隐式表示. 注意,对于多变量系统,这种隐式表示可能都不足以表明是否存在整数解. 根据马季亚谢维奇(Matiyasevich)关于希尔伯特第十问题的解 [2],这种情况应该可以预见的.
形如 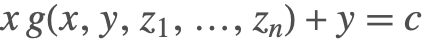 的方程
的方程
来求解,其中 ![]() 是不等式或者 True 的合取.
是不等式或者 True 的合取.
所得到的系统 (4) 可能会也可能不会被较容易地解出. 能够以任意次数迭代应用这种变换的系统是存在的,因此 Wolfram 语言使用一种迭代界限(recursion bound)来确保这种试探法能够终止.
能够通过穷举搜索求解的系统
对于所有变量都有明确的上下界的系统,Wolfram 语言通过穷举搜索来找到解. 搜索的界限通过系统选项 ExhaustiveSearchMaxPoints 的值设定. 选项的值应该是一对整数(默认值是 ![]() ). 如果界限内整数点的个数不超过第一个整数,则使用穷举搜索,而不是除一元多项式求解外的其它任何方法. 其它情况时,如果界限内整数点的个数不超过第二个整数,则穷举搜索在所有其他方法都失败后使用.
). 如果界限内整数点的个数不超过第一个整数,则使用穷举搜索,而不是除一元多项式求解外的其它任何方法. 其它情况时,如果界限内整数点的个数不超过第二个整数,则穷举搜索在所有其他方法都失败后使用.
选项
Wolfram 语言中用于求解丢番图多项式系统的函数有一系列的选项来控制其运行方式. 本教程对这些选项作一总结.
选项名称 | 默认值 | |
| GeneratedParameters | C | 指定如何对新生成的用于表示解的参数命名 |
影响丢番图多项式系统的行为的 Reduce 选项.
GeneratedParameters
为表示某些丢番图系统的无穷多个解,Reduce 需要引入新的整数参数. 新参数的名字通过选项 GeneratedParameters 设定. 在设置为 GeneratedParameters->f 时,新参数被命名为 f[1], f[2], … .
系统选项的 ReduceOptions 组
这里是 ReduceOptions 组中的系统选项,这些选项可能影响到用于丢番图多项式系统的 Reduce、Resolve 和 FindInstance 的行为. 这些选项可以用如下方式设置
SetSystemOptions["ReduceOptions"->{"option name"->value}].
选项名称 | 默认值 | |
| "BranchLinearDiophantine" | True | Reduce 是否使用分定支界型算法来计算线性丢番图不等式有界系统的解 |
| "DiscreteSolutionBound" | 10 | 在实数区间上明确列出整数解的个数的界限 |
| "ExhaustiveSearchMaxPoints" | {1000,10000} | 用于确定在使用所有其它解法之前及之后进行穷举搜索的变量界限内整数点数目的最大值 |
| "ImplicitIntegerSolutions" | Automatic | 当不能找到明确整数解时,Reduce 是否被允许返回带有 Element 条件的实解 |
| "LatticeReduceDiophantine" | True | 是否使用 LatticeReduce 对线性丢番图不等式的有界系统进行预处理 |
| "MaxFrobeniusGraph" | 1000000 | Frobenius 方程中,最小系数使 FindInstance 对 Frobenius 图中的临界树进行计算的最大值 |
| "SieveMaxPoints" | {10000,1000000} | 用于确定使用模筛法在所有其他解法前后求解系统的点数的最大值 |
影响丢番图多项式系统中的 Reduce、Resolve 和 FindInstance 的行为的 ReduceOptions 组选项.
BranchLinearDiophantine
系统选项 BranchLinearDiophantine 的值设定在求解有界线性系统的最后一步中使用算法的何种变体. 在默认设置 "BranchLinearDiophantine"->False 下,使用一种简单的递归枚举法. 在设置 "BranchLinearDiophantine"->True 下,Reduce 使用一种结合了分定支界型算法和简单递归枚举法的混合方法.
DiscreteSolutionBound
系统选项 DiscreteSolutionBound 的值对于整数解在实数区间 ![]() 内是明确列出,还是以
内是明确列出,还是以 ![]() 的形式隐式表示进行设定. 设置为 DiscreteSolutionBound->n 时,若数目不超过 n,给定实数区间内的整数解将明确列出. 该选项的默认值为10.
的形式隐式表示进行设定. 设置为 DiscreteSolutionBound->n 时,若数目不超过 n,给定实数区间内的整数解将明确列出. 该选项的默认值为10.
DiscreteSolutionBound 的值同时影响着求解有界线性方程组及其他具有有限多个解的丢番图系统. 在您需要在有界区域内对数目庞大的解进行显式枚举时,将 DiscreteSolutionBound 设置为 Infinity.
ExhaustiveSearchMaxPoints
系统选项 ExhaustiveSearchMaxPoints 设定穷举搜索法所用的搜索点的最大数目. 选项值应该是一对整数(默认值为 ![]() ). 如果界限内的整数点的个数不超过第一个整数,则使用穷举搜索,而不是其它任何方法(一元多项式的求解除外). 其它情况时,如果界限内整数点的个数不超过第二个整数,则在所有其他方法都失败后使用穷举搜索.
). 如果界限内的整数点的个数不超过第一个整数,则使用穷举搜索,而不是其它任何方法(一元多项式的求解除外). 其它情况时,如果界限内整数点的个数不超过第二个整数,则在所有其他方法都失败后使用穷举搜索.
ImplicitIntegerSolutions
系统选项 DiscreteSolutionBound 的值指定在实数区间 ![]() 上的整数解是显式枚举,还是隐式表示为
上的整数解是显式枚举,还是隐式表示为 ![]() . 在设置 DiscreteSolutionBound->n 时,在已知实数区间上的整数解如果数目不超过 n,则被显式枚举. 选项的默认值为10.
. 在设置 DiscreteSolutionBound->n 时,在已知实数区间上的整数解如果数目不超过 n,则被显式枚举. 选项的默认值为10.
LatticeReduceDiophantine
系统选项 LatticeReduceDiophantine 的值设定是否使用 LatticeReduce 对有界线性不等式系统进行预处理. 对于所描述的多面体在某些非坐标轴的直线上的投影比在坐标轴上的投影要小得多的不等式系统,LatticeReduce 的使用非常重要. 然而对于有些系统,LatticeReduce 的使用非但不能简化问题,反而会使难度显著增加.
MaxFrobeniusGraph
系统选项 MaxFrobeniusGraph 用于设定 Frobenius 方程中,最小系数使 FindInstance 使用基于计算 Frobenius 图中临界树 [11] 的算法的最大位数. 其它情况下,使用的是更一般的求解有界线性系统的方法. 与求解有界线性系统的一般方法不同,这种基于 Frobenius 图的计算的方法与变量数目几乎无关,因此对于存在很多变量的方程,这是一种较快的选择. 而另一方面,由于该方法要求存储一个具有最小系数大小的图,对于大型系数,可能会耗尽内存.
SieveMaxPoints
系统选项 SieveMaxPoints 设定的是模筛法及在带有一个线性变量的方程中所用的搜索的搜索点的最大数目. 选项的值是一个数对 ![]() . 在尝试一些较慢的解法之前,对涉及至多
. 在尝试一些较慢的解法之前,对涉及至多 ![]() 个点进行搜索. 对于决策问题,将在所有其他方法失败之后,尝试对涉及至多
个点进行搜索. 对于决策问题,将在所有其他方法失败之后,尝试对涉及至多 ![]() 个点的另一种搜索. 该选项的默认值是10,000.
个点的另一种搜索. 该选项的默认值是10,000.