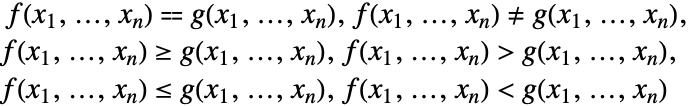はじめに

実多項式系とは，整方程式および不等式で構築された式

を，下のように論理結合子および量限定子を使って結合したものである．

変数 が または 内に現れることを束縛出現， がその他の部分に現れることを自由出現という．実多項式系に変数 の自由出現がある場合， はその系の自由変数という．実多項式系に量限定子が含まれない場合は，quantifier freeという．

以下は，自由変数 ，， を持つ実多項式系の例である．

実多項式系はすべて，冠頭標準形

に変換することができる．ここで，それぞれの は または であり， は系のquantifier free部分と呼ばれる量限定子のない式である．

量限定子のない実多項式系はすべて，選言標準形

に変換することができる．ここで，それぞれの は整方程式，あるいは不等式である．

Reduce，Resolve，FindInstanceは常に，quantifier-free部分が選言標準形で表して，実多項式系を冠頭標準形にする．それから方程式と不等式の両辺を減算して

という形式にする．このチュートリアルでは，常に系が上の形式に変換されているものと想定する．

Reduceは，任意の実多項式系を解くことができる．自由変数 を持つ系では，解（ について を拡張した後）は，以下の形式

の項の選言である．ここで は以下のいずれかである．

また，および は，を満足するすべての について正しく定義され（つまり，Rootオブジェクトの分母と主要項が非零），および は実数値を持ち，連続であり，不等式 を満足するような代数関数（Rootオブジェクトあるいは根号を使って表される）である．

式(4)で記述された の部分集合は，セルと呼ばれる．実多項式系の解の異なる項で記述されるセルは，独立である．

以下で について を拡張する関数を定義する：

Resolveは任意の実多項式系から量限定子を除去することができる．入力で変数が指定されておらず，すべての入力の多項式が束縛変数において最大で二次式であるならば，Resolveは結果の系を解かずに量限定子を除去することができることもある．そうでなければ，ResolveはReduceと同じアルゴリズムを使い，同じ答を出す．

FindInstanceは任意の実多項式系を扱うことができ，実数解の例，あるいは空リスト（解のない系の場合）を与える．複数の例が要求された場合，例は系のすべての解からランダムに生成されるので，RandomSeedオプションの値に依存する可能性がある．1つの例が要求され，系に全称記号()が含まれていない場合は，1つの例だけを生成するより高速なアルゴリズムが使われ，返される例は常に同じものになる．

実多項式系を解くときに一般的に用いられる主なツールは，CAD (Cylindrical Algebraic Decomposition)である（例えば[1]を参照のこと）．実多項式系に対するCADは，Wolfram言語ではCylindricalDecompositionで直接利用することができる．この他にも特殊な問題を解くために使われるアルゴリズムもある．

CAD法

半代数集合とセル分割

の部分集合が，量限定子を含まない実多項式系の解集合である場合，それは半代数集合である．タルスキー(Tarski)の定理[2]によれば，任意の（量化された）実多項式系の解集合は半代数集合である．

すべての半代数集合は，以下のように再帰的に定義された独立のセルの有限結合[3]として表すことができる．

• のセルは，点あるいは開区間である．
• のセルは，以下の2つの形式のうちのどちらかである．

ここで は のセル， は連続の代数関数，と は連続の代数関数，， のいずれかであり， では が成り立つ．

代数関数とは関数 で，その関数についての多項式

が

となるようなものを言う．Wolfram言語では，代数関数はRootオブジェクトあるいは無理式で表すことができる．

CAD法はCollins[4]によって提唱されたもので，任意の実多項式系の解集合のセル分割を計算する．元来のCollinsのアルゴリズムの目的は，量化された実多項式系から量限定子を除去して，量限定子を含まない等価の多項式系を生成することであった．アルゴリズムはセル分割を見付けた後，自由変数の整方程式および不等式による半代数集合の陰的表現を探索するという別のステップを実行した．Reduceの目的は多少これとは異なる．実多項式系で提示される半代数集合があると，Reduceはそれが量化されているかどうかに関わらず，代数関数で明示的に書かれたその集合のセル分割を見付ける．

Reduceは系を解くために他の方法を使うことがあるが，CylindricalDecompositionはCAD法に直接アクセスする．実多項式系では，CylindricalDecompositionはセルの選言を表すネストされた公式を，解形式(4)で与える．Reduceの出力と同様に，セルは独立であり，その上，後続の変数の範囲について常に辞書順に並べられる．

SemialgebraicComponentInstancesは，半代数集合のそれぞれの接続要素において少なくとも1つの標本点を与える．この関数はCADアルゴリズムを使い，構築されたセルのそれぞれにおけるサンプル点を返す．

CAD法の投影段階

CAD法を使って半代数集合のセル分解を見付ける場合，射影とリフティングの2つの段階がある．射影では，系(2)のquantifier-free部分 に存在する多項式の因数の集合 から始め，

が成り立つような射影演算子 を使って，変数をひとつひとつ除去する．一般に， の多項式すべてがセル で一定の符号なら，の多項式すべてが 上で描写可能である．つまり，各多項式が の多項式として 上に一定数の実根を持ち，根は 上で連続関数であり，根は一定の多様性を持ち，2つの多項式の2つの根は において常に等価であるか，決して等価にならないかのどちらかであるということである．変数は

という順で並ぶ．これで， の多項式の根は半代数集合のセル分解の構築に必要な代数関数となる．

もとのCollins射影の大きさは，向上された結果より小さくなった．現在，すべての場合に適用可能な最善の射影演算子はHong [5]によるものである．しかし，ほとんどの場合，McCallum [6, 7]が提唱し，Brown [8]が改善した，これより小さい射影演算子を使うことができる．特殊な場合に適用できるさらに小さい演算子もある．等式制約がある場合は，Collins [9]が提案し，McCallum [10, 11]が改善・証明した射影演算子を使うことができる．厳密な不等式だけで方程式がない場合，および，自由変数がない，または半代数集合の完全次元部分にしか関心がない場合は，[12, 13]で記述してあるさらに小さい射影演算子を使う使うことができる．また，0次元イデアルを生成する等式制約を含む系では，グレブナー基底(Gröbner bases)を使って射影多項式を見付ける．

Wolfram言語は与えられた例題に対して，上述の適切な射影のなかで最小のものを使う．できる限り，等式制約を使用するが，等式制約を使用しないときは，Brownが改善したMcCallumの射影を試みる．系がうまくいかない場合は，Hongの射影を計算する．

CAD法のリフティング段階

リフティング段階では，半代数集合のセル分解を見付ける．一般に，実際の詳細は使用される射影演算子に依存するが，の異なる根すべてと根の間の開区間で構成されるの中のセルから開始する．各セルに標本点を見付け，半代数集合を記述する系（系には だけを含む条件が付いている場合がある）を満足しない標本点を持つセルを削除する．次にそのセルを のセルまで一度に一次元ずつリフティングする．セルを までリフティングしたとしよう．セル をまでリフティングするために， に の標本点 の座標が代入された の実根を見付ける．多項式 は 上で描写可能なので，各根 は における連続の代数関数の値であり，その関数は が の 番目の根となるような多項式 の 番目の根として表すことができる．ここでセル をまでリフティングする作業には，これらの代数関数のグラフ，および後続のグラフ間の ×のスライスが含まれる．それぞれの新セルの標本点は，根のひとつと等価である ，あるいは2つの連続する根の間の数に， 番目の座標を加えることにより得られる．第1段階で行ったように，リフティングされたセルのうち，半代数集合を記述する系を満足しない標本点を持つものは削除する．

ならば， は量限定子変数であり，リフティングされたセルをすべて構築する必要はないかもしれない．必要なのは， 上の の真値（必ず定数）を求めることだけである．ならば，リフティングされたセルのいずれかにおいて の真値がTrueであるとすぐに，値がTrueであることが分かる． ならば，リフティングされたセルのいずれかにおいて の真値がFalseであるとすぐに値がFalseであることが分かる．

このようにして計算された標本点の係数は，一般に代数的数である．コストの高い代数的数の計算を避けるために，Wolfram言語では結果の妥当性が認められる限り，任意精度の浮動小数点数(Wolfram言語"bignum")による係数近似を使う．単独あるいはペアの多項式の2つの根が異なることを証明したり，標本点で多項式の非零符号を見付けたりする場合には，近似演算を使っただけで十分なことがある．近似演算で証明できないのは，単独あるいはペアの多項式の2つの根が等しいこと，あるいは標本点において多項式がゼロであること等である．しかし，セルの起源についての情報を使えば，このような問題が解けることが多い．例えば，2つの多項式の終結式がセル上で消失し，これらの多項式が等しい可能性のある1組の複素根を精度範囲内に持つならば，これらの根は等しいと結論付けることができる．同様に，標本点の最後の座標が，与えられた多項式の因数の根であるなら，この多項式は標本点においてゼロであるということが分かる．セルに関して集めた情報を使っても不確実性をすべて解決できない場合は，座標の厳密な代数的数値を計算する．詳細は[14, 24]を参照のこと．

決定問題，FindInstance，仮定

決定問題とは，すべての変数が存在量化された系である．つまり，

という形式の系のことである．ここで はすべて の変数となっている．決定問題を解くことは，それがTrueとFalseのどちらと等価であるかを判定すること，言い換えれば，量限定子を含まない整方程式および不等式の系 が解を持つかどうかを判定することである．

Wolfram言語で実多項式の決定問題を解くために使用するアルゴリズムはすべて，系に解がある場合に を満足する点を生成することができる．従って，このセクションで説明するアルゴリズムは，単独の例が要求され，系に量限定子が含まれていない，あるいは存在記号しか含まれていない場合は常に，決定問題に対してReduceおよびResolveだけではなく，FindInstanceでも使われる．また，このアルゴリズムはSimplify，Refine，Integrate等，仮定を使うWolfram言語関数で，推論検定のために使われる．

以下の決定問題を解くことで，集合 に，原点を中心とする半径4/5の円板が含まれることが証明される：

以下は， に単位円板が含まれないことを示し， に属さない単位円板上の点があるという反証を挙げている：

Wolfram言語で任意の実多項式の決定問題を解くために使える主なメソッドはCAD (Cylindrical Algebraic Decomposition)法である．しかし，この他にも，使用可能な場合にはCADよりもよいパフォーマンスを提供する特殊な場合のアルゴリズムがいくつかある．

多項式がすべて有理数係数あるいは浮動小数点数係数に比例する場合，Wolfram言語ではシンプレックス線形計画法に基づくメソッドが使われる．他の線形系では，Loos-Weispfenningの線形量限定子除去法[15]の変形が使われる．系に方程式がなく，厳密な不等式だけが含まれている場合は，CAD法の高速な「一般」形が使われる[12, 13]．0次元イデアルを生成する等式制約を含む系では，解の探求にグレブナー基底が使われる．浮動小数点数係数の非線形系には，CADの非厳密係数バージョン[16]が使われる．

また，他の決定問題法の前処理として使える特殊な場合のメソッドもある．系に，ひとつの変数の定数係数に比例する等式制約が含まれる場合，線形変数の除去にこの制約が使われる．系に定数係数と比例して現れる変数しかない場合は，その変数はLoos-Weispfenningの線形量限定子除去法[15]で除去される．二次の系にしか現れない変数がある場合は，その変数を除去するためには仮の代入法[22, 23]によるWeispfenningの量限定子除去の二次法が使われる．この方法で非常にスピードアップする例もあるが，ほとんどの場合はかなりスピードが落ちる．デフォルトでは，このアルゴリズムは前処理としては使われない．InequalitySolvingOptionsグループのシステムオプションQVSPreprocessorをTrueにすると，Wolfram言語はこれを使うようになる．

Wolfram言語には，この他にも特殊な場合の実多項式の決定問題法が2つある．まず，Aubry，Rouillier，Safey El Dinによるアルゴリズム[17]は方程式のみを含む系に適用される．このアルゴリズムの方がCAD法よりも格段に速く実行できる例もあるが，ランダムに選ばれた方程式系では，パフォーマンスがかなり劣ることが多い．従って，これはデフォルトでは使われない．InequalitySolvingOptionsグループのシステムオプションARSDecisionをTrueに設定すると，Wolfram言語でそのアルゴリズムが使われるようになる．また，G. X. ZengとX. N. Zengによるアルゴリズム[18]は，単独の厳密な不等式で構成される系に適用される．ここでも，このアルゴリズムの方がCAD法よりも速くなる例もあるが，一般には遅くなる．従って，これもデフォルトにはなっていない．InequalitySolvingOptionsグループのオプションZengDecisionをTrueに設定すると，このアルゴリズムが使われる．

任意の実多項式系

実多項式系を解く

タルスキーの定理[2]によると，任意の（量化された）実多項式系の解集合は，半代数集合である．Reduceはこの集合を解形式(4)で記述する．

以下は，がどのようなときに，集合 が原点を中心とする半径 の円板を含むかを示している：

以下は 軸に沿った 平面上に を射影する：

次は 軸に沿った 平面上にホイットニーの傘(Whitney umbrella) を射影する：

量限定子除去(QE)

変数が指定されていないResolveの目的は，量限定子を除去して，量限定子を含まない等価の式を生成することにある．その式は，使用されるアルゴリズムによって，解形式の場合もあれば，そうでない場合もある．

ここでは，入力にある ，， の多項式が複雑であるため，量限定子を含まない式を完全な解形式で生成することは難しい．しかし， は入力の多項式で線形にのみ現れるので，係数の複雑性にほとんど依存しないLoos-Weispfenningの線形量限定子除去法を使うと，量限定子を即座に除去することができる：

アルゴリズム

Wolfram言語で実多項式系およびそのQEを解くために使われる主なメソッドは，CAD法である．しかし，特殊な場合にはこれよりも簡単な方法が使える．

系に最内部の量限定子の変数についての等式制約が含まれていれば，以下の恒等式

を使って系を簡約化するために，その等式制約が使われる．ここで あるいは が非零の定数である場合，変数 が除去される．

系の多項式すべてが最内部の量限定子の変数に比例する場合は，変数はLoos-Weispfenningの線形量限定子除去法[15]を使って除去される．

系の多項式すべてが，最も内側の量限定子からの変数について最大でも二次である場合は，仮の代入アルゴリズム[22, 23]によるWeispfenningの量限定子除去の二次法を使って変数が除去される．システムオプションQuadraticQEのデフォルト設定では，変数を指定せず少なくとも2つのパラメータを持つResolveに対して，また，1つの変数の除去がシステムのLeafCountを最大でも2倍にする限りにおいて少なくとも3つの変数を持つReduceおよびResolveに対して，このアルゴリズムが使われる．

上記3つの特殊な場合のメソッドが適用されない場合には，CAD法が使われる．しかし，まだ除去すべき量限定子が残っているか，解が要求されるかのいずれかである．

0次元イデアルを生成する等式制約を含む系には，Wolfram言語では解集合を見付けるためにグレブナー基底が使われる．

オプション

実多項式系を解くWolfram言語関数には，操作方法を制御するオプションが数多く備わっている．このセクションでは，そのようなオプションを要約する．

実多項式系への操作に影響を与えるReduce，Resolve，FindInstanceのオプション

CubicsとQuartics

その理由は，カルダノの公式は実数解とそれ以外の解とを分離しないためである．例えば，以下で，のときは3番目の有理解が実数であるが，のときは最初の有理解が実数である：

WorkingPrecision

WorkingPrecisionの設定はCAD法のリフティング段階に影響を及ぼす．有限の作業精度 prec では，リフティングされる第1変数の標本点が，prec 桁精度で任意精度の浮動小数点数として表される．連続した変数の標本点を計算すると，すでに計算された標本点の座標に依存するしているために，厳密ではない可能性のある係数を持つ多項式の根が見付かる．従って，標本点の座標の精度は prec 以下となる．標本点における多項式の符号を判別するためには，代入後に得られる浮動小数点数のSignを評価するだけでよい．有限のWorkingPrecisionを使うと，答はより速く得られる．しかし，答が誤っていたり，精度の損失により計算が失敗したりする可能性がある．

ReduceOptionsグループのシステムオプション

ここで挙げるのは，実多項式系でのReduce，Resolve，FindInstanceの動作に影響を及ぼすReduceOptionsグループのシステムオプションである．これらのオプションは以下のように設定する．

SetSystemOptions["ReduceOptions"->{"option name"->value}].

実多項式系でのReduce，Resolve，FindInstanceの動作に影響を及ぼすReduceOptionsグループのオプション

零次元イデアル を生成する方程式制約を持つ系の場合，Wolfram言語はグレブナー基底メソッドを使って投影多項式を見付けるCADアルゴリズムの変形を使う． のグレブナー基底の辞書式順序が，最後の変数以外のすべての変数に定数係数の線形多項式を含んでいるならば，解のすべての座標は一つの代数的数の多項式，つまり最後の座標である．AlgebraicNumberOutputの設定は，Reduceが解の座標を最後の座標によって生成された場のAlgebraicNumberオブジェクトとして表すかどうかを決定する．

オプションFactorEquationsは，入力の前処理段階で下の変換

を使うかどうかを指定する．デフォルト設定のFactorEquations->Automaticでは，自動ヒューリスティックにより決定される．

入力の前処理段階で，以下のような変換

を使うと，計算が速くなることがある．しかし，これは一般に問題を解きやすくする訳ではない．さらには，問題を顕著に難しくしてしまうこともある．この変換はデフォルトでは使われない．

デフォルトではSolveは指定された変数の順序を変えることができる．この例では， について解いてから の解で を表す方が簡単である：

InequalitySolvingOptionsグループのシステムオプション

ここで挙げるのは，実多項式系でのReduce，Resolve，FindInstance，CylindricalDecompositionの動作に影響を及ぼすInequalitySolvingOptionsグループのシステムオプションである．これらのオプションは以下のように設定する．

SetSystemOptions["InequalitySolvingOptions"->{"option name"->value}].

オプション名	デフォルト値
"ARSDecision"	False	[17]で与えられた決定アルゴリズムを使うかどうか
"BrownProjection"	True	[8]で与えられた向上射影演算子をCAD法で使うかどうか
"CAD"	True	CAD法を使うかどうか
"CADBacksubstitution"	Automatic	CAD法が解座標の数値を代入しなおすべきかどうか
"CADCombineCells"	True	CAD法の出力を，解の公式が同一となっている範囲の隣接セルを結合することによって，簡約するかどうか
"CADConstruction"	Automatic	CADの構築メソッドを指定する
"CADDefaultPrecision"	30.103	CAD法のリフティング段階で計算される非有理根の初期の精度．近似根での計算が妥当とされない場合，アルゴリズムは精度を"CADExtraPrecision"の値だけ引き上げる．これで問題が解決しない場合は，厳密な代数的数の計算に戻る
"CADExtraPrecision"	30.103	CAD法のリフティング段階で使われる追加の精度
"CADMethod"	Automatic	CylindricalDecompositionで使われるCAD計算メソッドを指定する
"CADSortVariables"	Automatic	単独の量限定子もしくは決定問題の量限定子変数に対して，CAD法で変数順序のヒューリスティックを使うかどうか
"CADZeroTest"	{0,∞}	代数的数の座標の点で多項式を評価することによって得られた式について，CAD法で使うゼロ検定法を決定する
"EquationalConstraintsCAD"	Automatic	CAD法の投影段階で等式制約を使うかどうか．デフォルトのAutomatic設定では，[11]で正しいと証明された演算子が使われる．Trueの場合は，[4]で提案された複数の等式制約を使った証明されていない投影演算子が使われる
"FGLMBasisConversion"	False	0次元のブレブナー基底の単変数多項式を求めるために，CADで[20]に基づくグレブナー基底変換法を使うかどうか．使わない場合はGroebnerWalkが使われる
"FGLMElimination"	Automatic	等式制約が0次元イデアルを形成する系に対する決定およびQEアルゴリズムで，除去に使われる変数のひとつの線形等式制約（定数主要係数）を探すために，[20]に基づくアルゴリズムを使うかどうか
"GenericCAD"	True	決定および最適化問題で，[13]に記述されているCAD法の変形を使うかどうか
"GroebnerCAD"	True	等式制約が0次元イデアルを形成する系に対するCAD法で，射影としてグレブナー基底を使うかどうか
"LinearDecisionMethodCrossovers"
	{0,30,20,Automatic}	実数係数を持つ線形方程式および不等式系の解を見付けるために使用するメソッドを決定する
"LinearEquations"	True	決定問題の変数を除去するために，線形等式制約（定数の主要係数）を使うかどうか
"LinearQE"	True	QE問題に対してLoos-Weispfenningの線形量限定子除去法[15]を使うかどうか
"LWDecision"	True	線形不等式系を持つ決定問題に対して，Loos-Weispfenningの線形量限定子除去法[15]を使うかどうか
"LWPreprocessor"	Automatic	決定問題の前処理として，Loos-Weispfenningの線形量限定子除去法[15]を使うかどうか
"ProjectAlgebraic"	Automatic	CAD法で代数的数の係数に代入される変数についての射影を計算するか，その最小多項式を使うか
"ProveMultiplicities"	True	CAD法のリフティング段階で投影方程式の複数根と零主係数を証明する方法を決める
"QuadraticQE"	Automatic	QEのバーチャル代入法により，Weispfenningの量限定子除去の二次法を使うかどうか
"QVSPreprocessor"	False	バーチャル代入法によるWeispfenningの量限定子除去の二次法を決定問題の前処理として使うかどうか
"ReducePowers"	Automatic	CAD法の入力で を で置換するかどうか．ここで は系の のすべての指数のGCDである
"RootReduced"	False	0次元イデアルを形成する等式制約を持つ系の解座標を単独のRootオブジェクトに還元するかどうか
"Simplex"	True	線形不等式系の決定アルゴリズムで，シンプレックス法を使うかどうか
"SimplifyInequalities"	Automatic	[25]で提示されている不等式簡約化のヒューリスティックを使うかどうか
"ThreadOr"	True	量限定子を含まない系を解く必要がない場合に，決定問題，最適化，存在記号のQEにおけるそれぞれの選言を別々に解くかどうか．
"ZengDecision"	False	[18]で与えられる決定アルゴリズムを使うかどうか

実多項式系でのReduce，Resolve，FindInstanceの動作に影響を及ぼすInequalitySolvingOptionsグループのオプション

デフォルトではWolfram言語は，解の公式が同一となっている隣接したセルを結合することによりCADアルゴリズムの結果を簡約化する．ここでは，解集合は結合されていないが， の解の公式はすべての実数 について同じである：

投影多項式は結合されたセル上で描写できない場合がある．例えば，ここでは と は において共通根を持っているが，区間の他の点においては共通根を持っていない：

CADConstructionの設定は，すべての関数におけるCADアルゴリズムを使った直接のCAD構築に使われる方法を決定する．Wolfram言語には2つの異なるCAD構築アルゴリズムの実装が含まれている．CADConstruction"GlobalProjection"では，共通の投影が1回計算されてすべてのセルの構築に使われる[4, 24]．CADConstruction"LocalProjection"では，それぞれのセルに対してローカルの投影が計算される[28]．CADConstruction"Parallel"では2つのカーネルが起動し，両方のメソッドが並列で実行される．デフォルト設定のCADConstructionAutomaticでは，少なくとも2つのサブカーネルが利用可能な場合は両方のメソッドが並列で実行され，そうでない場合はヒューリスティックを使ってメソッドが選ばれる．

CADMethodの設定はCylindricalDecompositionにより使われるCAD計算メソッドを指定する．これはCADアルゴリズムを使う他の関数には影響しない．デフォルト設定のCADMethod->Automaticは設定DirectとRecursiveを組み合せたものである．

厳密な代数的数の座標を持つ標本点が使われると，このオプションの設定がCAD法のリフティング段階に影響を及ぼす．デフォルトではWolfram言語は任意精度の浮動小数点数の座標を持つ標本点を使い，[14, 24]のメソッドを使ってその結果の正当性を立証する．厳密な代数的数の座標を持つ標本点は，近似計算の結果の正当性が立証されない場合か，CADDefaultPrecisionがInfinityに設定されている場合にのみ使われる．

代数的数の座標での標本点で評価された多項式の符号を判定するためには，まず代数的数の数値近似で多項式を評価する．この結果が非零（つまり，ゼロが結果の近似数の誤差範囲内にない）であれば，符号は分かる．そうでない場合は，代数的数での多項式がゼロであるかどうかを検定する必要がある．CADZeroTestオプションの値により，このとき使うゼロ検定法を指定する．値は， というペアになる．デフォルト値の では，Wolfram言語は式がゼロであればゼロとなるような確度 を計算する． ならば，式の値が確度 まで計算されて，その符号がチェックされる．さもなくば，式はRootReduceを使って単一のRootオブジェクトとして表され，Rootオブジェクトの符号が見付けられる．デフォルト値の では，eacc>$MaxPrecisionの場合RootReduceに戻る．であれば，RootReduceが常に使われる．ならば，確度 までゼロである式は零とみなされる．これが最も速いメソッドであるが，他の2つとは異なり，誤った結果を与える可能性がある．それは，非零であってもゼロに近い式がゼロとして扱われている可能性があるためである．

EquationalConstraintsCADオプションは，CAD法の投影段階で等式制約を使うかどうかを指定する．デフォルト設定のAutomaticでは，Wolfram言語は[11]で正しいと証明された投影演算子を使う．EquationalConstraintsCAD->Trueでは，[4]で提案された小さいが，証明されていない投影演算子が使われる．

Wolfram言語は0次元イデアル を生成する等式制約を持つ系では，ブレブナー基底を使って射影式を見付けるCAD法の変形法を使う．辞書式順序の のグレブナー基底が，最後の変数以外のすべての変数に定数係数を持つ線形多項式を含まず，UseNestedRootsがFalseにされているならば，各変数 について に属する の一元多項式を見付ける．Wolfram言語はこれを2つの方法で行う．デフォルトでは，GroebnerWalk演算に基づいたメソッドを使う．FGLMBasisConversionをTrueに設定すると，Wolfram言語は[20]に基づくメソッドを使う．

FGLMEliminationオプションは，0次元イデアル を生成する等式制約を持つ系に適用できる特殊な場合のヒューリスティックを，Wolfram言語で使用するかどうかを指定する．このヒューリスティックは，[20]に基づくメソッドを使って， の中に量化変数のひとつについて線形な（定数係数を持つ）多項式を見付け，除去のためにその多項式を使う．このメソッドは，決定アルゴリズムでもQE法でも使うことができる．デフォルトのAutomatic設定では，「解く」変数が指定されていないResolve，および少なくとも自由変数を2つ持つ系でのみ使うことができる．

Wolfram言語は[13]で記述されたCAD法の簡約化バージョンを使って，決定問題を解き，方程式を含まない実多項式系の解を求める．このメソッドは解を求め，系の不等式すべてが厳密（ または ）である場合に解がないことを証明するものである．このメソッドは弱い（ または ）不等式を含む系にも使うことができる．しかし，その系の厳密な不等式バージョンに解がないことが証明すると，もとの系に解があるかどうかを判別するためにCAD法が必要になる．システムオプションGenericCADは，Wolfram言語でこのメソッドを使うかどうかを指定する．

0次元イデアルの を生成する等式制約のある系には，Wolfram言語はグレブナー基底を使って射影式を求めるCADの変形法を使う．GroebnerCADをFalseと設定すると，Wolfram言語は標準のCAD射影を使う．

この3つのオプションは，決定問題を解くため，または線形方程式および不等式の系の解の例を見付けるために使われる．利用可能なメソッドにはLoos-Weispfenning法[15]，シンプレックス法，改訂シンプレックス法がある．この3つのメソッドはすべて，有理係数および浮動小数点数係数を持つ系を扱うことができる．厳密な非有理係数を持つ系では，Loos-Weispfenning法だけが実装される．LWDecisionはLoos-Weispfenning法が使用可能かどうかを指定する．Simplexはシンプレックス法と改訂シンプレックス法が使えるかどうかを指定する．LinearDecisionMethodCrossoversは，すべてのメソッドが使用可能，適用可能である場合に，どのメソッドを使うかを決定する．オプションの値はリストでなければならない．Wolfram言語では， 変数までの線形系には，Loos-Weispfenning法[15]が使われる．から 変数の系にはシンプレックス法が， 変数より多い系には改訂シンプレックス法が使われる．シンプレックス法が使われる場合，不等式の数が変数の数の 倍に満たないとき， がTrueかAutomaticのとき，系が厳密なときは，スラック変数が使われる．デフォルト値は ，，，s==Automaticである．

LinearEquationsオプションは，定数の主係数を持つ線形等式制約を変数除去のために使用するかどうかを指定する．この設定は一般にアルゴリズムのパフォーマンスを向上させる．このオプションは，「純粋な」CADベースの決定アルゴリズムの実験を可能にするために提供されている．

ここでWolfram言語は，CADを使って結果となる2変数の系の解を求める前に，第一方程式を使って を除去する：

LinearQEオプションは，系のすべての方程式および不等式のなかで最も線形に現れる最内部の量限定変数を，少なくとも1つ含む系を扱うために使われる．オプション設定は，決定問題の解決には影響を与えない．デフォルト設定のTrueでは，Wolfram言語はLoos-Weispfenning法[15]を使って，系で線形にのみ現れる量限定変数をすべて除去する．その後，量限定子が残っている場合，あるいは結果を自由変数について解く必要がある場合は，CAD法が使われる．LinearQE->Automaticと設定すると，Loos-Weispfenning法は，系で定数係数を持ち，線形にのみ現れる変数に対してのみ使われる．LinearQE->Falseとすると，Loos-Weispfenning法は使用されない．

デフォルト設定のLinearQE->Trueでは， と の両方を除去するためにはLoos-Weispfenning法が使われ，二変数の量限定子を含まない残りの系を解くためにはCAD法が使われる：

LinearQE->Automaticと設定すると， を除去するためだけにLoos-Weispfenning法が使われ，三変数の残りの系を解くためにはCADが使われる．この例では，デフォルトのメソッドの方がずっと速い：

以下は，デフォルトメソッドの方が速くない場合の例である．デフォルト設定のLinearQE->Trueでは， と の両方を除去するためにLoos-Weispfenning法が使われ，量化変数と自由変数をそれぞれ1つずつ持つ残りの系を解くためにはCAD法が使われる．今回は，デフォルトメソッドが最高速ではない：

LinearQE->Automaticとすると， を除去するためだけにLoos-Weispfenning法が使われ，量化変数2つと自由変数1つを持つ残りの系を解くためにはCAD法が使われる：

LWPreprocessorオプション設定は，決定問題の解決と例の探索に影響を与える．このオプションは，結果の系にCAD法を適用する前に，Loos-Weispfenning法[8]を使って，すべての等式および不等式で最も線形に現れる変数を除去するかどうかを指定する．デフォルト設定のAutomaticでは，Wolfram言語はLoos-Weispfenning法を使って，定数係数を持ち，線形にのみ現れる変数を除去する．LWPreprocessor->Trueとすると，Loos-Weispfenning法は線形にのみ現れる変数すべてに使用される．LWPreprocessor->Falseでは，Loos-Weispfenning法はCADベースの決定法の前処理として使用されない．

デフォルト設定のLWPreprocessor->Automaticでは，Loos-Weispfenning法は を除去するためだけに使用され，三変数の残りの系の解を求めるためにはCAD法が使われる：

LWPreprocessor->Trueと設定すると， と の両方を除去するためにLoos-Weispfenning法が使われ，二変数を持つ残りの系の解を求めるためにはCAD法が使われる．以下の例では，このメソッドはデフォルトのものより遅い：

以下の例は，最後の不等式が等式になっていること以外，前の例と同じである．デフォルトのLWPreprocessor->Automaticでは，Loos-Weispfenning法は を除去するためだけに使われ，3変数の残りの系の解を見付けるためにはCAD法が使われる：

LWPreprocessor->Trueとすると，Loos-Weispfenning法は と の両方を除去するために使われ，二変数の残りの系の解を見付けるためにはCAD法が使われる．改訂したこの例では，このメソッドの方がデフォルトよりも速い：

ProjectAlgebraicオプションの設定は，CAD法の代数的数の係数の取扱いに影響を及ぼす．

入力系の係数で見付かった代数的数は，新しい変数で置き換えられる．この新しい変数は常に変数順の最初に置かれるので，CAD法の投影段階では最後に除去される．現在の射影式に 個の変数が含まれており，少なくとも最初の 個が代数的数の係数に取って代る場合，射影を継続するかどうかを選ぶことができる．射影段階を継続しない場合は，それぞれの変数が対応する代数的数の係数に等しいという関係が成り立つ，最初の 個の変数の0次元セルを拡張するリフティング段階を開始することができる．最後の の射影を計算することを選択した場合は，リフトされている変数に当たる代数的数の係数が射影式の根の間に存在することが，リフティング段階で分かる．従って，この変数については0次元セルを有理数の標本点で拡張することになる．このように，最後の の射影の計算を避けることと，標本点での代数的数による座標を避けることとの間には，トレードオフがある．

ProjectAlgebraic->Trueと設定すると，残りの変数が1つになるまで，代数的数による係数を置換する変数について射影段階が続く．ProjectAlgebraic->Falseと設定すると，代数的数による係数を置換しない変数が1つ残ると同時に，射影段階が終了する．デフォルト設定のProjectAlgebraic->Automaticでは，代数的数の係数を置換しない変数が多くて1つ残っており，少なくとも3つの射影式または射影変数の次数が2より大きい射影式がある場合に，射影段階が終了する．

ProveMultiplicitiesの設定は，CAD法のリフティング段階で任意精度の浮動小数点数（Wolfram言語の"bignum"）計算（詳細は[14, 24]を参照）を使って得た投影多項式の多根および主係数0を証明する方法を決定する．デフォルト設定のProveMultiplicities->Trueでは，Wolfram言語はセルの原点についての情報を使う．これで十分ではない場合は，セル座標の厳密値を計算し，部分終結式の主係数と厳密な零検定を使う．これで失敗したときのみ，厳密計算に戻る．ProveMultiplicities->Automaticでは，Wolfram言語はセルの原点の情報を使い，それで十分でない場合は厳密計算に戻る．ProveMultiplicities->Falseでは，無限桁の整数の計算がすべての根の分離に失敗するたび，あるいは投影多項式の主係数が非零であることを証明するのに失敗するたびに，Wolfram言語は厳密計算に戻る．

QuadraticQEオプションは，仮の代入アルゴリズム[22, 23]によるWeispfenningの量限定子除去の二次形式を使って，系のすべての方程式および不等式で最大でも二次的に現れる量化変数を除去するかどうかを指定する．すべての変数の数において二重指数的であるCAD法の複雑さとは異なり，Weispfenningのアルゴリズムの複雑さは，自由変数の数にはほとんど依存しない．従って，すべての量限定子がこのアルゴリズムを使って除去できる場合，多数の自由変数が存在する場合，量限定子を含まないタイプの系が解形式で与えられる必要のない場合には，これを使った方が確実によい．しかしながら，Weispfenningのアルゴリズムを使って変数を除去すると，式の大きさを顕著に大きくしてしまうので，Wolfram言語が結果にCADを適用しなければならない場合や系にほとんど自由変数が含まれていない場合は，もとの系にCADを使った方が速い． デフォルト設定のAutomaticでは，Wolfram言語は変数の指定されていない，あるいは少なくとも2つの変数のあるResolve，および1つの変数の除去が系のLeafCountを最大でも二倍にする限りにおいて少なくとも3つの変数を持つReduceとResolveに対してこのアルゴリズムを使う．この分類はかなりうまくいくようであるが，これが最適のアルゴリズムとはならない場合もある．オプション値を変更することで，非常に長時間かかるであろう問題を解くことができる場合がある．QuadraticQE->Trueという設定では，除去しなければならない二次変数がある場合は常にWeispfenningのアルゴリズムが使われ，QuardaticQE->Falseでは使われない．

変数が指定されていない，あるいは少なくとも2つのパラメータを持つResolveでは， を除去するのにWeispfenningのアルゴリズムが使われる．結果はパラメータ ，， について解かれない：

このReduceの例についてはデフォルトでCAD法が使われる．結果はパラメータ ，， について解かれる：

QuadraticQE->Trueと設定すると，Reduceで を除去するのにはWeispfenningのアルゴリズムが，パラメータ ，， に対する量限定子のない式を解くのにはCAD法が使われる．この例では，はじめからデフォルトメソッドのCADを使うよりも速い：

QVSPreprocessorオプション設定は，決定問題を解く場合とインスタンスを見付ける場合に影響する．このオプションは，結果となる系にCADアルゴリズムを適用する前にすべての方程式および不等式で最大で二次で現れる変数を除去するために，仮の代入アルゴリズム[22, 23]によるWeispfenningの量限定子削除の二次形式を使うかどうかを指定する．デフォルト設定はFalseであり，このアルゴリズムは使用されない．前処理としてWeispfenningのアルゴリズムを使うことでパフォーマンスが顕著に向上する例もあるし，前処理を使うことによりパフォーマンスが著しく低下する例もある．前処理は多数の変数がある例やインスタンスが存在する例で効果を発揮する傾向がある．QVSPreprocessor->Trueと設定すると，二次変数があるたびにWeispfenningのアルゴリズムが使われ，QVSPreprocessor->Automaticと設定すると，少なくとも4つの変数を持つ系に対してこのアルゴリズムが使われる．

CAD法の入力に含まれる変数 は，その系に表れる のすべてのベキ乗が整数 の整数倍である場合，Wolfram言語は入力系の を新しい変数で代替し，新しい系でCAD法を実行してから，もとの変数で表現されるように解を求める．ReducePowers->Falseと設定すると，このショートカットがオフになる．ReducePowers->Falseという設定では，CAD法の出力におけるセルの範囲として現れる代数関数は，常に有理関数，二次無理式，Rootオブジェクトのいずれかになる．デフォルトのReducePowers->Trueでは，これに加えて，以前の任意の式 に対しては ，整数 および有理関数または二次無理式 に対してはRoot[a#ⁿ-e&,1]となることがある．

デフォルト設定のReducePowers->Trueでは，CAD法は と に代る変数で二次方程式を解き，結果を および で表す．結果には，内部に二次無理式を持つRootオブジェクトが含まれている：

0次元イデアル を生成する等式制約を含む系では，Wolfram言語はグレブナー基底法を使って射影多項式を求めるCAD法の変形を使う． の辞書式順序のグレブナー基底に，最後の変数以外のすべての変数（一般に真である）に定数係数を持つ線形多項式が含まれている場合，解の座標すべてが最後の座標の多項式で簡単に表される．それ以外の場合は，座標は三角方程式系によって定義された代数的数を表すRootオブジェクトとして与えられる．RootReducedをTrueに設定すると，Wolfram言語は各座標を，最小の多項式と根の数によって定義された1つの数値的なRootオブジェクトとして表す．この簡約表現の計算は，系を解くよりも格段に時間がかかることが多い．

デフォルトでは， で表現された の値を得る：

Backsubstitution->Trueと設定すると，AlgebraicNumber表現で与えられる の数値を得る：

RootReduced->Trueと設定すると，Wolfram言語は の値を1つのRootオブジェクトとして表す．しかし計算にはもっと時間がかかる：

RootReduced->Trueと設定すると，Wolfram言語は の値を，最小多項式と根の数によって定義されたRootオブジェクトとして表す．しかし，計算にはより時間がかかる：

デフォルト設定のSimplifyInequalities->Automaticでは，Wolfram言語は[25]で提示されている不等式の簡約化ヒューリスティックを使ってCADアルゴリズムへの入力を簡約化し，CADの投影因子の不等式を推定する．その後，その不等式を使って投影段階で非零の係数と部分終結式を認識し，リフティング段階でセルを削除する．ヒューリスティックは仮想代入アルゴリズム[15, 23]の中間結果を簡約化するのにも使われる．SimplifyInequalitiesをTrueに設定すると，不等式簡約化ヒューリスティックが追加の変換 を実行する．SimplifyInequalities->Falseでは，不等式簡約化ヒューリスティックは使われない．

オプションThreadOrは，決定アルゴリズム（自由変数あるいはパラメータを含まない系ではReduceとResolve），FindInstance，QE（変数指定のないResolve)において，以下の恒等式

をどのように使うかを指定する．デフォルト設定のThreadOr->Trueでは，恒等式(8)は解法を試みる前に使われる．ThreadOr->Falseとすると，恒等式(8)はその使用を必要とするアルゴリズム（シンプレックス法等）によって使われることがある．しかし，その使用を必要としないアルゴリズム（CAD法等）では使われない．

参考文献