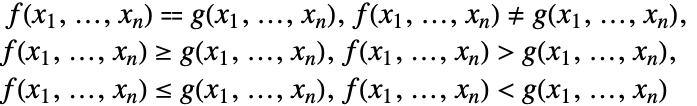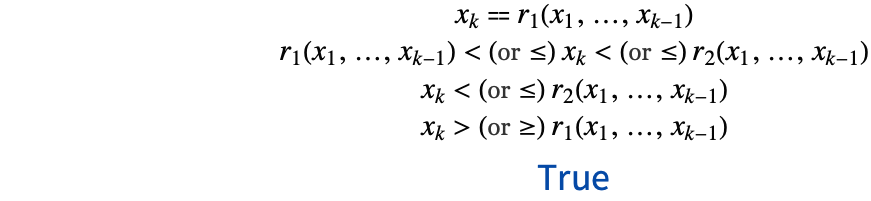实数多项式系统

介绍任意实数多项式系统
柱形代数分解选项
决策问题、FindInstance 和假设参考文献

介绍

实数多项式系统是由多项式方程和不等式

结合逻辑运算符和量词

所构建的表达式.

在 或 内部出现的变量 称为约束出现；任何其它情况下 的出现都称为自由出现. 如果实数多项式系统含有变量 的自由出现，则变量 被称作该系统的自由变量. 如果一个实数多项式系统不含量词，则该系统为无量词系统.

下面的例子是一个含有自由变量 、 和 的实数多项式系统.

任何实数多项式系统都可变换成前束范式

其中 是 或 ，并且 是称为系统中无量词部分的无量词公式.

任何无量词实数多项式系统都可变换成析取范式

其中 是多项式方程或不等式.

Reduce、Resolve 以及 FindInstance 总是把实数多项式系统化为前束范式，无量词部分化为析取范式，并将等式或不等式的两边相减，化成这种形式

在本教程中，我们都假定系统已被转换成上述形式.

Reduce 可以求解任意实数多项式系统. 对于带有自由变量 的系统，所得到的解 (可能已将 关于 展开) 是下述形式中各项的析取:

其中 是

中的一个，并且 和 是代数函数（用 Root 对象或根表示），满足对所有满足 的 ， 和 有确切的定义（即分母和 Root 对象的首项不能为零）、有实数值、连续并满足不等式 .

由公式（4）描述的 的子集被称为一个单元. 由实数多项式系统的解的不同项所描述的单元是不相交的.

这里解出了系统（1）. 单元用嵌套形式表示：
这里定义了相对于 展开 的函数：
这是以不相交单元的集合显式写出的系统（1）的解：

Resolve 可以消除任意实数多项式中的量词. 如果在输入时不指明变量并且所有的输入多项式至多对约束变量是二次的，Resolve 可能能够在不解出结果系统的情况下消去量词. 否则，Resolve 使用与 Reduce 相同的算法并给出相同的答案.

这里从系统（1）中消去了量词：

FindInstance 可以处理任意实数多项式系统，给出实数解的实例或者在无解情况下给出一个空列表. 如果要求的实例数大于1，这些实例将从系统的全部解集中随机生成，因此可能将取决于选项 RandomSeed 的值. 如果只需一个实例并且系统不包含一般量词（），将使用的是一种更快的算法，并且返回的实例永远相同.

这里得到系统 (1) 的一个解：

求解实数多项式系统的主要工具是柱形代数分解（CAD）算法 (见例[1]等). 在 Wolfram 语言中，对于实数多项式系统有 CAD 可以直接使用，即 CylindricalDecomposition. 对于特殊情形的问题还有一些其它算法可用.

柱形代数分解

半代数集合和单元分解

如果 的子集是无量词实数多项式系统的解集，则称其为半代数的. 根据 Tarski 定理[2]， 任意（量化）的实数多项式系统的解集为半代数的.

每一个半代数集都可以表示为下述递归形式定义的有限个不相交单元[3]的并集：

  • 中的一个单元是一个点或一个开区间
  • 中的一个单元采用下述形式之一：

其中 是 中的一个单元， 是一个连续代数函数， 和 是连续代数函数或者 或 ，并且在 上， .

所谓的代数函数，指的是一个函数 ，对于这个函数存在一个多项式

使得

在 Wolfram 语言中，代数函数可以表示成 Root 对象或者根.

由 Collins [4] 引入的 CAD 算法用于计算任意实数多项式系统的解集的单元分解. Collins 算法的最初目的是从一个量化的实数多项式系统中消去量词，并且生成等价的无量词多项式系统. 在得到一个单元分解后，该算法执行一个附加步骤，以自由变量的多项式方程和不等式的形式找到一个半代数集的隐式表示. Reduce 的目的有所不同. 给定一个由实数多项式系统表示的半代数集，不管其被量化与否，Reduce 找到集合的一个单元分解，以代数函数的形式显式写出.

Reduce 可以使用其它方法对这个系统求解，但 CylindricalDecomposition 提供了CAD 算法的直接途径. 对于实数多项式系统，CylindricalDecomposition 给出了一个嵌套公式，以解出的形式（4）表示的单元析取. 而在 Reduce 的输出中，单元是不相交的，并且关于后继变量的范围其次序总是字典序.

这里得到了一个圆环（annulus）的单元剖分：

SemialgebraicComponentInstances 给出半代数集的每个连通分支上至少一个样本点. 该函数使用 CAD 算法，返回每个构建单元的一个样本点.

这里给出圆环单元剖分的一个样本点：

CAD 算法的投影阶段

使用 CAD 算法得到一个半代数集的单元分解由两个阶段组成，投影和提升. 在投影阶段，以系统(2)的无量词部分 的多项式的因式的集合 开始，使用投影算符 逐个消除变量，使得

一般来说，如果 的所有的多项式在一个单元 有恒定的符号，则 的所有的多项式在 上是可描绘（delineable）的，也就是说，作为 中的一个多项式，每一个在 上都有固定数量的实根，这些根是 上的连续函数，具有恒定的重数，并且其中任意两个多项式的两个根在 上要么处处相等，要么处处不相等. 变量的排序使得

这样的话， 的多项式的根就是构建半代数集单元分解所需的代数函数.

一些改良减小了原始 Collins 投影的大小. 目前可应用于所有情形的最好的投影算符是由 Hong [5] 提出的；然而，在大多数情形下，可以使用由McCallum [6, 7] 提出、并被 Brown [8] 改良的一个较小的投影算符. 对于某些特殊情形，还有一些更小的投影算符. 如果有等式约束，则可使用有 Collins [9] 建议，并被 McCallum [10, 11] 发展和证明的投影运算符. 当没有等式，而只有严格不等式，并且无自由变量或者我们只关注半代数集的全维数部分（full-dimensional part）时，则可以使用[12, 13]中描述的更小的投影算符. 对于包含生成零维理想的等式约束的系统，将使用 Gröbner 基来得到多项式的投影.

Wolfram 语言使用先前提到的适用于给定例子的最小投影. 我们尽可能的使用等式约束；否则，将使用由 Brown 改良的 McCallum 的投影. 在系统的导向不好时，则计算 Hong 的投影.

CAD 算法的提升阶段

在提升阶段，我们将找到半代数集的单元分解. 一般来说，尽管具体细节取决于所用的投影算符，我们都将从 中由 的所有不同根以及根之间的开区间组成的单元开始. 在每一个单元中找到一个采样点，并去除采样点不符合描述半代数集的系统的单元（该系统可以包含只牵涉到 的条件). 下一步是将单元提升至 中的单元，一次一个维数.假设单元已被提升至 . 为了将一个单元 提升至 ，我们要找到 的实根并将 用 中采样点 的坐标替代. 由于 的多项式在 上不可描述，每一个根 是 处的一个连续代数函数的一个值，并且该函数可以用一个多项式 的第 个根表示，使得 为 的第 个根. 现在对单元 至 的提升将由这些代数函数的图及后续图中 × 的切片组成. 每一个新单元的采样点将通过在 中增加第 个坐标得到，该坐标等于其中的一个根，或是等于后面的两个根的之间的一个数. 和第一步相同，采样点不符合描述半代数集的系统的提升了的单元将被去除.

如果 ，则 是一个量词变量，此时可能不必构建所有的提升单元. 我们只需要找到 上 的（必为常数的）真假值. 如果 ，一旦 的真假值在其中一个提升单元上为 True，这个值就为 True. 如果 ， 则只需要 的真假值在其中一个提升单元上为 False，就可得出这个值为 False.

这样计算得到的采样点的系数通常是代数数. 为了节省高成本的代数数计算，Wolfram 语言在保证结果有效的前提下，对系数尽量使用任意精度浮点数 (Wolfram 语言 "bignum") 近法. 对于证明一个多项式的两根或一对多项式的不同，以及找到一个多项式在某个采样点的非零符号而言，使用近似运算可能就足够了. 用这种近似运算所不能证明的是一个多项式的两根或一对多项式的相等，或是一个多项式在某个采样点为零. 不过，这个问题常常可以通过利用单元来源的信息来解决. 例如，如果已知两个多项式的结式在该单元上为零，并且这两个多项式恰好有一对在精度范围内能够相等的复数根，可以得到两根相等的结论. 类似地，如果一个样本点的最后一个坐标为已给多项式的一个因式的根，则可得到该多项式在这个采样点为零. 如果无法利用所采集到的单元信息消除所有不确定性，则计算坐标的精确代数数值. 要了解更多细节，参见[14, 24].

决策问题、FindInstance 和假设

决策问题是所有变量全部被存在性量化的系统，即一个形如

的系统，其中 代表 中的所有变量. 解决一个决策问题意味着决定其是否等价于 True 或 False，也就是说，判断多项式方程和不等式 的无量词系统是否有解.

Wolfram 语言用于解决实数多项式决策问题的所有算法都能够在系统有解的情况下产生一个满足 的点. 因此本节讨论的算法不仅用在解决决策问题的 Reduce 和 Resolve 中，也用于 FindInstance，只要所要求的只是一个实例并且系统是无量词的或者只有存在性量词. 这里所讨论的算法还被 Wolfram 语言函数用于推论测评，使用诸如 Simplify、Refine、Integrate 等等的假设.

这个决策问题的求解证明集合 含有以原点为中心，半径为4/5 的圆盘：
这里表明 不含单位圆盘，并举出一个反例：单位圆盘内的一个点不属于 ：

允许 Wolfram 语言解决任意多项式决策问题的基本方法是柱形代数分解（CAD）算法. 然而还有一些其它特殊算法在适当的时候能够有更好的表现.

当所有的多项式对有理数或者浮点数系数为线性时，Wolfram 语言使用一种基于单纯型线性规划法的方法. 对于其它的线性系统，Wolfram 语言使用 Loos–Weispfenning 线性量词消去算法[15]的一种变形. 当系统不含等式且只有严格不等式时，将使用一种更快的“通用”版本的 CAD 算法[12, 13]. 对于含有生成一个零维理想的等式约束的系统，Wolfram 语言使用 Gröbner 基得到解. 对于带有浮点数字系数的非线性系统，使用的是CAD [16] 的一个粗略系数版本.

还有一些可以用作其它决策方法的预处理器的特殊方法. 当系统含有一个与其中一个变量的常系数呈线性关系的等式约束，则该约束用于消去该线性变量. 若在系统中存在一个变量只与常系数呈线性，则用 Loos–Weispfenning 线性量词消去算法[15]消去该变量. 若在系统中有一个只以二次形式存在的变量，变量的消去可以用 Weispfenning 量词消去的二次情形通过虚拟替代算法[22, 23]的来实现. 对于某些例子，这样做可以显著加快速度；然而在更多的时候这样做反而会使速度明显减慢. 默认设置下，该算法不用作预处理. 在 InequalitySolvingOptions 组中设置系统选项 QVSPreprocessor 为 True 可以使 Wolfram 语言采用这个算法.

在 Wolfram 语言中还存在两个特殊情形的实数决策算法. Aubry、Rouillier 和 Safey El Din [17] 提供了一个适用于只有方程的系统的算法. 对于一些例子，该算法比 CAD 算法好很多；然而，对于随机选择的方程系统，其表现似乎明显要差；因此在默认情况下不采用这种算法. 在 InequalitySolvingOptions 组中设置系统选项 ARSDecision 为 True 会使 Wolfram 语言采用这种算法. 另外一个算法由 G. X. Zeng 和 X. N. Zeng [18]提出，适用于由单一严格不等式组成的系统. 同样，这种算法对于某些例子有比 CAD 快，但通常速度较慢；因此它也不用于默认设置. 在 InequalitySolvingOptions 组中设置系统选项 ZengDecision 为 True 会导致 Wolfram 语言采用这种算法.

任意实数多项式系统

求解实数多项式系统

根据 Tarski 定理 [2]，任意（量化）实数多项式系统的解集为半代数集. Reduce 以解出的形式（4）给出这个解集的一个描述.

这里显示出对于什么样的 ，集合 包含中心为原点，半径为 的圆盘：
这里给出 沿着 轴在 平面上的投影：
这里得到了Whitney 伞（Whitney's umbrella） 沿着 轴在 平面上的投影：
这里直接通过定义得到了上述投影集合的内部：

量词消去

如果没有指定变量， Resolve 的目的是消去量词并生成一个等价的无量词公式. 根据所用算法的不同，该公式可以是，也可以不是一个解出的形式.

这里由于出现在输入中的关于 、 和 的多项式的复杂性，生成一个完全解出的无量词公式是困难的. 然而，由于 只在输入的多项式中线性出现，可以使用 Loos–Weispfenning 线性量词消去算法快速地消去量词，而与系数的复杂性几乎无关：

算法

对于求解实数多项式系统和实数量词的消去，Wolfram 语言所使用的基本算法是 CAD 算法. 而在一些特殊情形时，还有一些更简单的算法.

如果系统包含一个相对最内层的量词的变量的等式约束，这个约束可以用来通过使用下述恒等式对系统进行简化

如果 或 为非零常数，就消去了变量 .

如果系统内的所有多项式对于在最内层的量词的一个变量是线性的，则用 Loos–Weispfenning 线性量词消去算法 [15] 消去该变量.

如果系统中的所有多项式对于在最内层的量词的一个变量至多是二次的，则该变量的消去由 Weispfenning 量词消去的二次情形通过虚拟替代算法[22, 23]来实现. 使用系统选项 QuadraticQE 的默认设置时， Resolve 使用该算法解决无指定变量并且至少有两个参数的情形，Reduce 和 Resolve 使用该算法解决三个变量以上的情形，只要一个变量的消去至多使系统的 LeafCount 翻倍.

如果上述三种特殊情形的方法不适用，但是还是会有一些量词有待消去或是需要一个解，则使用 CAD 算法.

对于包含生成一个零维理想的等式约束的系统，Wolfram 语言使用 Gröbner 基来寻找解集.

选项

对用于求解实数多项式系统的 Wolfram 语言函数，有一些选项来控制函数的运行方式. 本节对这些选项作一总结.

选项名称
默认值
CubicsFalse是否用 Cardano 公式表示三次方程的数值解
QuarticsFalse是否用 Cardano 公式表示四次方程的数值解
WorkingPrecision∞计算使用的工作精度

Reduce、Resolve 和 FindInstance 中影响实数多项式系统的行为的选项.

三次方程和四次方程

默认情况下，Reduce 不使用 Cardano 公式求解实数上的三次方程和二次方程：
设置选项 Cubics 和 Quartics 为 True 使得 Reduce 使用 Cardano 公式来表示三次方程和四次方程的数值解：
包含参数的三次方程和四次方程的解将仍用 Root 对象表示：
这是因为 Cardano 公式不能将实数解从非实数解中分开. 例如下面这种情形，对于 ，第三个基数解为实数，但对于 ，第一个基数解为实数：

WorkingPrecision

WorkingPrecision 的设置影响到 CAD 算法的提升阶段. 对于一个有限的工作精度 prec，提升的第一个变量的采样点由精度位数为 prec 的任意精度浮点数表示. 当计算后面的变量的采样点时，所找到的多项式的根的系数由已经算出的采样点的坐标得到，因此有可能并不准确. 这样采样点的坐标精度将为 prec 或更低. 采样点处的多项式的符号的确定简单地通过确定替换后的浮点数的符号 Sign 来完成. 使用有限的工作精度 WorkingPrecision，可能能更快地得到结果，但是结果可能会错误，或者由于精度的丧失而导致计算失败.

这里 Reduce 中使用 WorkingPrecision->30，得到正确的解，其速度要比使用无穷的WorkingPrecision 快：

系统选项的 ReduceOptions 组

这里是 ReduceOptions 组中可能影响到实数多项式系统的 Reduce、Resolve 和 FindInstance 的行为的系统选项. 这些选项可以用以下方式来设置

SetSystemOptions["ReduceOptions"->{"option name"->value}].
选项名称
默认值
"AlgebraicNumberOutput"TrueReduce 是否输出 AlgebraicNumber 对象，而不是一个 Root 对象中的多项式
"FactorEquations"Automatic在输入预处理阶段是否应该分解方程
"FactorInequalities"False是否将不等式在输入预处理阶段作因式分解
"ReorderVariables"Automatic是否允许 Reduce、Resolve 和 Solve 对指定变量重新排序
"UseNestedRoots"Automatic表示由三角方程组定义的代数数的 Root 对象是否能够用于输出

影响实数多项式系统的 Reduce、Resolve 和 FindInstance 的行为的 ReduceOptions 组选项.

AlgebraicNumberOutput

对于具有生成零维理想 的等式约束的系统，Wolfram 语言使用 CAD 算法的变形，利用 Gröbner 基方法求投影多项式. 如果 的字典序 Gröbner 基所含的线性多项式中，除最后一个变量外，其他变量均为常系数（一般而言确实如此），则解的全体坐标是一个单一代数数（即最后一个坐标）的多项式. AlgebraicNumberOutput 的设置确定 Reduce 是否用由最后一个坐标生成的域中的 AlgebraicNumber 对象表示解坐标.

在默认情况下，解坐标表示为 AlgebraicNumber 对象：
设置为 AlgebraicNumberOutput->False 时，解坐标以 Root 对象中的多项式的形式给出：

FactorEquations

选项 FactorEquations 指定变换

是否应该用在输入的预处理阶段. 在默认设置 FactorEquations->Automatic 下由自动启发式决定.

这里 Reduce 不使用变换：
使用变换会加速第一个范例；然而，使得第二个范例减速：

FactorInequalities

在输入预处理阶段使用变换

在一些情形下可能会加快计算速度. 但这种方法通常并不能简化问题的解决，甚至在某些情况下这样做会显著增加问题的难度. 在缺省设置下，不采用这种变换.

这里 Reduce 不使用（7）中的变换：
使用变换（7）在第一个例子中起到加速作用，但使是第二个例子的速度显著减慢. 第二个例子受到不等式数目指数增长的影响：

ReorderVariables

默认设置时的 Reduce 不能给指定变量重新排序. 变量列表中先出现的变量可以用来表示后出现的变量的解，但反之不行：
设置系统选项 ReorderVariables->True 允许 Reduce 选择一个合适的变量次序来简化系统的求解：
默认情况下，允许 Solve 对指定变量重新排序. 在这个例子中，先求解 ，再用 的解表示 ，较为较简单：
设置系统选项 ReorderVariables->False 使得 Solve 使用指定的变量顺序：

UseNestedRoots

默认情况下，Reduce 能将解表示为 Root 对象的形式，表示由三角方程组定义的代数数：
设置系统选项 UseNestedRoots->False 使得 Reduce 使用由一元方程定义的代数数：
求所有解坐标的最小多项式，速度会比较慢：
设置 UseNestedRoots->True 允许 Reduce 使用由对于最后一个变量为线性的三角方程组定义的代数数：
在默认设置 UseNestedRoots->Automatic 下，Reduce 将第二个坐标表示为第一个坐标内的多项式：

系统选项的 InequalitySolvingOptions 组

这里是 InequalitySolvingOptions 组中可能影响到实数多项式系统的 Reduce、Resolve、FindInstance 和 CylindricalDecomposition 的行为的系统选项. 这些选项可以用以下方式设置

SetSystemOptions["InequalitySolvingOptions"->{"option name"->value}].
option name
default value
"ARSDecision"False是否使用 [17] 中给出的判决算法
"BrownProjection"TrueCAD 算法是否应该使用 [8] 中给出的改善的射影算子
"CAD"True是否使用 CAD 算法
"CADBacksubstitution"AutomaticCAD 算法是否应该回带解坐标的数值值
"CADCombineCells"TrueCAD 算法的输出是否应该通过在解公式相同的情况下组合相邻单元进行简化
"CADConstruction"Automatic指定 CAD 构建方法
"CADDefaultPrecision"30.103初始精度中的非有理根是在 CAD 算法的提升阶段进行计算；如果带有近似根的计算不能被验证，算法会通过 "CADExtraPrecision" 的值增加精度；如果这样不能解决问题，算法会恢复为精确代数值计算
"CADExtraPrecision"30.103CAD 算法的提升阶段使用额外的精度数量
"CADMethod"Automatic通过 CylindricalDecomposition 指定使用的 CAD 计算方法
"CADSortVariables"Automatic对于单个量词或决策问题中的量词变量，CAD 算法是否应该使用变量重排序试探法
"CADZeroTest"{0,∞}对于通过在带有代数数值坐标的点计算多项式获得的表达式，确定 CAD 算法使用的零测试方法
"EquationalConstraintsCAD"AutomaticCAD 算法的投影相位是否应该用于等式约束；默认的 Automatic 设置使用 [11] 中证明正确的算子；如果是 True，使用 [4] 中建议的用于多个等式约束的未证明的投影算子
"FGLMBasisConversion"FalseCAD 算法是否应该使用基于 [20] 的 Gröbner 基转换算法来求0维 Gröbner 基的单变量多项式；否则，使用 GroebnerWalk
"FGLMElimination"Automatic对于带有等式约束形成0维理想的系统，决策和量词消除算法是否使用基于 [20] 的算法查找（带有常首项系数的）线性方程约束，其中一个变量被用于消除
"GenericCAD"True对于决策和优化问题是否用 [13] 中描述的 CAD 算法变体
"GroebnerCAD"True对于带有等式约束形成0维理想的系统，CAD 算法是否使用 Gröbner 基作为投影
"LinearDecisionMethodCrossovers"
{0,30,20,Automatic}决策方法用于求解线性方程和带有有理数系数的不等式系统的解
"LinearEquations"True是否使用（带有常首项系数）的线性方程约束消除决策问题中的变量
"LinearQE"True对于量词消除问题是否使用 Loos–Weispfenning 线性量词消除算法[15]
"LWDecision"True对于带有线性不等式的系统是否使用 Loos–Weispfenning 线性量词消除算法[15]
"LWPreprocessor"Automatic是否使用 Loos–Weispfenning 线性量词消除算法[15]作为决策问题的预处理器
"ProjectAlgebraic"AutomaticCAD 算法是否应该计算关于变量的投影，取代代数数或使用最小多项式
"ProveMultiplicities"True确定 CAD 算法的提升阶段验证投影多项式的多重根和零首项系数的方法
"QuadraticQE"Automatic是否通过量词消除中的虚拟替代算法使用 Weispfenning 量词消除的二次情形
"QVSPreprocessor"False是否通过虚拟替代算法使用 Weispfenning 量词消除的二次情形作为决策问题的预处理器
"ReducePowers"Automatic是否在 CAD 的输入中用 替代 ，其中 是系统中 所有指数的 GCD
"RootReduced"False带有等式约束形成零维理想的系统的解的坐标是否应该化简为单个 Root 对象
"Simplex"True对于线性不等式系统的决策算法是否使用单纯型算法
"SimplifyInequalities"Automatic是否使用[25]中的不等式简化试探法
"ThreadOr"True是否在决策问题、优化以及当无量词系统不需要求解时的存在量词的量词消除中分别求解析取的每种情况
"ZengDecision"False是否使用[18]中的决策算法

影响实数多项式系统的 Reduce、Resolve 和 FindInstance 的行为的 InequalitySolvingOptions 组选项.

ARSDecision

选项 ARSDecision 设定 Wolfram 语言是否使用由 Aubry、Rouillier 和 Safey El Din [17] 给出的算法. 该算法适用于只含方程的决策问题. 对于一些例子，该算法比 CAD 算法好很多；然而，对于随机选择的方程系统，其效果似乎明显要差；因此在默认情况下不采用这种算法. 这里是一个决策问题 （文献中称为 butcher8），CAD 在1000秒内不能完成，而用[17] 给出的算法却成很快地算出：

BrownProjection

采用默认设置时，Wolfram 语言中 CAD 算法的执行采用的是 Brown 的改良投影算符 [8]. 这个改良通常能显著加快计算速度. 而在某些情形下，使用 Brown 的改良投影算符会使速度稍微有所减慢.选项 BrownProjection 设定是否使用 Brown 的改良投影算符. 在第一个例子中 [21]，使用 Brown 的改良投影算符使得运行速度增快；而在第二个例子中，速度则减缓：

CAD

选项 CAD 设定是否允许 Wolfram 语言采用 CAD 算法. 将 CAD 设置为 False 时， 要求使用 CAD 的计算将立即失败，而不会尝试高复杂性的 CAD 计算. 启用 CAD 后，该计算无法在1000秒内完成：

CADBacksubstitution

默认情况下，Wolfram 语言返回替代 CAD 算法中解坐标的有理值. 其它数值则不会被返回替代：
在设置 CADBacksubstitution->True 时，所有解坐标的数值被返回替代：
在设置 CADBacksubstitution->False 时，Wolfram 语言不会返回替代 CAD 算法中的坐标值：

CADCombineCells

默认情况下，Wolfram 语言合并解式相同的相邻单元，从而对 CAD 算法的结果进行简化. 这里 的解式对于所有实数 是相同的，即使解集不连通亦如此：
在设置 CADCombineCells->Automatic 时，Wolfram 语言仅当解式不含 Root 函数时，合并解式相同的相邻单元. 这保证在 CylindricalDecomposition 的结果的析取中分布合取时，每一个合取说明一个连通集：
投影多项式在合并后的单元上可能是不能界定的. 比如，这里的 和 在 处有一个公共根，但在区间 的其他点处是没有公共根的：
在设置 CADCombineCells->False，Wolfram 语言不合并 CAD 单元：

CADConstruction

CADConstruction 的设置确定使用 CAD 算法的所有函数中的直接 CAD 构建使用的方法. Wolfram 语言包含两个不同 CAD 构建算法的实现. 当 CADConstruction"GlobalProjection"，普通投影被计算一次并用于构建所有单元[4, 24]. 当 CADConstruction"LocalProjection"，每个单元计算局部投影[28]. 当 CADConstruction"Parallel"，启动两个子内核，并行尝试两种方法. 默认设置 CADConstructionAutomatic，如果至少有两个子内核可用，那么会并行尝试两种方法；否则的话，使用试探法选择一种方法.

以下使用 "GlobalProjection" 方法：
这个例子中，"LocalProjection" 方法更快：
自动方法用试探法选择 "GlobalProjection" 方法：
使用可用子内核尝试两种方法：

CADDefaultPrecision 和 CADExtraPrecision

采用默认设置时，Wolfram 语言在 CAD 算法的提升阶段采用经验证有效的数值计算，仅在数值计算无法被验证的情况下才转为精确代数计算[14, 24]. 选项 CADDefaultPrecision 设定计算采样点坐标的初始精度. 如果该精度下进行的计算无法被验证，算法将把精度值提高值 CADExtraPrecision. 如果这不能解决问题，算法将转向精确代数数计算. 对 CADDefaultPrecision 和 CADExtraPrecision 的值的选择是在数值计算的速度和由精度丧失而转为精确计算的点数之间作出的权衡. 采用缺省的100位元（bit）的设置，由精度丧失而转为精确计算法的情形是很罕见的. 将 CADDefaultPrecision 设置为Infinity 使 Wolfram 语言在 CAD 算法的提升阶段使用精确代数计算. 这个例子中，将 CADDefaultPrecision 设置为最低值，运行速度最快. (将值设定的低于16.2556 (54 位元) 导致 CADDefaultPrecision 设定为16.2556.) CADDefaultPrecision->Infinity 的设置使得该例无法在1000秒内完成：

CADMethod

设置 CADMethod 决定用于 CylindricalDecomposition 的 CAD 计算方法. 这不影响其他使用 CAD 算法的其他函数. 默认设置 CADMethod->Automatic 是 Direct 和 Recursive 设置的结合.

在设置 CADMethod->Direct，CylindricalDecomposition 计算柱形代数分解，将 CAD 算法单次应用到转换为前束格式的输入公式：
在设置 CADMethod->Recursive 下，CylindricalDecomposition 对输入公式进行细分，计算每一个子式的 CAD，然后利用[26]的算法合并结果：
如果输入公式是一个合取式，则在设置 CADMethod->Iterative 下，CylindricalDecomposition 计算合取式的第一个元素的 CAD，然后利用[27]的算法将合取式的后续元素叠加：

CADSortVariables

CAD 算法的性能常在很大程度上取决于所用的变量的次序. 变量排序的某些方面是被所解问题固定了的：量词变量需要在自由变量之前被投影，最内层量词的变量需要最先被投影. 除非ReorderVariables 的设置为 True，否则 在 Reduce 和 Resolve 中指定的变量不能被排序. 然而量词的排序还是留有一些自由度的：来自同一量词的变量和提供给 FindInstance 的变量都可以重新排序. 默认设置时，Wolfram 语言使用一种变量排序试探法来决定这些变量的顺序. 大多数时候，该试探法能够改善 CAD的性能；然而有些时候该试探法却无法选出最好的次序. 将 CADSortVariables 设置为 False，使这种试探法实效，变量的顺序由量词变量列表给出，或者是在 FindInstance 的变量列表参数中给出. 这个例子 [21] 中，如果不对量词变量重新排序，就无法使计算在1000秒内完成：
这里给出了该例最优的变量排序：

CADZeroTest

该选项的设置影响着使用精确代数数坐标的采样点的 CAD 算法的提升阶段. 在默认情况下，Wolfram 语言使用带有任意精度浮点数坐标的采样点，并利用[14, 24] 的方法验证结果. 具有精确代数数坐标的采样点仅在不能验证近似计算结果时或 CADDefaultPrecision 设置为 Infinity 时被采用.

要确定在一个具有代数数坐标的采样点处运算的多项式的符号，首先计算代数数的数值近似处的多项式. 如果结果非零（即零点不在所产生的近似数的误差范围内），则符号可知. 否则需要测试代数数值的多项式表达式是否为零. CADZeroTest 选项的值设定此时使用何种零测试法.该值应该是一个数对 . 在默认值 时，Wolfram 语言计算准确度 ，使得若该表达式在此准确度内为零，则其必定为零. 如果 ，则计算在准确度 内的表达式的值，并检查其符号. 在其他情况下，使用 RootReduce 将该表达式表示为一个单一的 Root 对象，从而得到 Root 对象的符号. 对默认值 ，如果 eacc>$MaxPrecision，转化为 RootReduce. 若 ，始终使用 RootReduce. 如果 ，在准确度 以内为零的表达式被认为是零. 这是最快的方法，但与另外两个不同，它可能给出错误结果，因为非零但接近于零的表达式可能会被误认为是零..

在设置 CADDefaultPrecision->Infinity 下，CAD 算法使用精确代数数坐标的采样点：
该例使用30位精度零测试的 CAD 算法，运行速度较快. 该例的结果是正确的，然而CADZeroTest 的这种设置可能会导致错误结果：
在系统选项的默认设置下，这个例子的运行速度显著加快：

EquationalConstraintsCAD

选项 EquationalConstraintsCAD 对 CAD 算法的投影阶段是否使用等式约束进行设定. 默认设置 Automatic 是，Wolfram 语言使用经 [11] 证实的投影算符. 设置 EquationalConstraintsCAD->True 使得[4] 中提到的较小但未经证实的投影运算符被采用.

这里我们用设置为EquationalConstraintsCAD->True 的 CAD 算法找到了一个满足系统的解. 尽管求解的方法是基于一个未经证实的猜想，但可以证明其结果是正确的，即结果满足输入的系统：
使用默认设置 EquationalConstraintsCAD->Automatic，系统的求解需要的时间有些长：
使用设置 EquationalConstraintsCAD->False 时，系统的求解需要更长的时间：
这里 FindInstance 显示系统无解. 由于使用的是设置为 EquationalConstraintsCAD->True 的 CAD 算法，结果的正确与否取决于一个未证实的猜想：
使用默认设置 EquationalConstraintsCAD->Automatic 时，证实系统无解需要更长的时间，但结果是正确的：

FGLMBasisConversion

对于带有生成一个零维理想 的等式约束的系统，Wolfram 语言使用一种 CAD 算法的变体，它采用 Gröbner 基方法来得到投影多项式. 如果 的字典序 Gröbner 基只含有对最后一个变量的带常系数的线性多项式，且 UseNestedRoots 的设置为 False，则对于每一个变量 ，我们得到一个属于 的关于 的一元多项式. Wolfram 语言采用两种方式来做到这一点. 默认情况下采用的是基于 GroebnerWalk 计算的方法. 将 FGLMBasisConversion 设置为 True 将使 Wolfram 语言采用一种基于[20]的方法.

一般情况下，这种基于[20]的方法似乎稍微有点慢：

FGLMElimination

FGLMElimination 选项设定 Wolfram 语言是否对带有等式约束，且该约束形成一个零维理想 的系统使用一种特殊情形的试探法. 该试探法使用一种基于 [20] 的算法，在 中找到对某一个量化变量线性（首系数为常数）的多项式，并用这种多项式进行量词消去. 这种方法既可用于决策算法也能用于量词的消去. 使用默认设置 Automatic，该算法仅用于未指定求解变量的 Resolve 中，且用于至少有两个自由变量的系统.

缺省情况下采用基于 [20] 的消去法，返回一个未求解形式的无量词系统：
将 FGLMElimination 设置为 False，该例计算时间延长，而结果是已解出的形式. （为读起来方便，显示的是结果的 N 形式.）
如果只有一个自由变量，缺省设置时的 Resolve 不采用基于 [20] 的消去法. （为读起来方便，我们以 N 形式显示结果）
将 FGLMElimination 设置为 True，该例计算时间延长，且结果是未解出的形式：

GenericCAD

Wolfram 语言使用 [13] 中描述的 CAD 算法的一种简化版本来解决决策问题或对不含方程的实数多项式系统求解. 当系统的所有不等式为严格不等式（ or ）时，该方法要么得到一个解，要么证明其无解. 这个方法也用于包含弱不等式（ or ）的系统. 这种情况时，如果得到了对应的严格不等式系统的解，则该解也将是原始系统的解. 然而，如果它证实该系统的严格不等式形式无解，则需使用CAD 算法的完全版本来对原始系统是否有解作出判定. 系统选项 GenericCAD 设定 Wolfram 语言是否使用这种方法.

这里 GenericCAD 方法得到了系统作为严格不等式版本时的解：
如果没有 GenericCAD，得到系统的解将需要更长的时间：
这个系统无解并且包含弱不等式. 在 GenericCAD 方法没有得到系统的严格不等式版本的解之后，Wolfram 语言需要运行完全版本的 CAD 来证实系统无解：
使用设置 GenericCAD->False 来运行同一例子节省了先前 GenericCAD 计算所用的时间：
该系统只包含严格不等式，因此 GenericCAD 能够证明其无解：
没有 GenericCAD，将需要更长的时间来证明系统无解：

GroebnerCAD

对于一个系统，该系统带有生成一个零维理想 的等式约束，Wolfram 语言使用 CAD 算法的变体，采用 Gröbner 基法来找到投影多项式. 将 GroebnerCAD 设置为 False 时，Wolfram 语言将转而使用标准 CAD 投影.

设置 GroebnerCAD->False，这个例子的运行速度要慢得多：
这里检查解的等价性：

LinearDecisionMethodCrossovers，LWDecision 和 Simplex

这三种选项用于设定求解决策问题或是找寻线性方程和不等式系统解的实例的方法. 可用的方法有：Loos–Weispfenning 算法 [15]，Simplex 算法和修正的 Simplex（Revised Simplex） 算法. 这三种方法都能够用于有理数系数或是浮点数系数的系统. 对于精确数值无理数系数的系统，只采用 Loos–Weispfenning 算法求解. LWDecision 设定 Loos–Weispfenning 算法是否可用. Simplex 设定 Simplex 算法和修正 Simplex 算法是否可用. LinearDecisionMethodCrossovers 在所有方法都可用并适用的情况下对使用何种方法做出决定. 选项的值是一个列表 . 对于变量个数小于或等于 的线性系统，Wolfram 语言使用 Loos–Weispfenning 方法[15]；若系统的变量个数在 和 之间，使用 Simplex 算法；对于变量个数大于 的系统，将使用修正 Simplex 算法. 如果使用的是 Simplex 算法，并且不等式的数目不大于变量数目的 倍，并且 为 True 或 为 Automatic 且系统是确切的. 将采用松弛变量（slack variable）. 三个数的默认值为 ，，，且 s==Automatic.

默认设置时， Simplex 算法被用于求解带有三个变量的线性系统：
这里使用的是修正 Simplex 算法：
这里使用的是 Loos–Weispfenning 算法：
由于 Simplex 算法和修正 Simplex 算法不用于带有精确无理系数的系统，这里使用了 Loos–Weispfenning 算法：
将 LWDecision 设置为 False， 且 Simplex 算法和修正 Simplex 算法都不适用, FindInstance 只好在此使用 CAD 算法：

LinearEquations

LinearEquations 选项用于设定是否用带有常数首系数的线性等式约束来消去变量. 这通常会改善算法的效能. 提供这个选项是为了允许对基于 “纯粹” CAD 的决策算法进行试验.

这里 Wolfram 语言先用第一个方程来消去 ，再用 CAD 找到所得带有两个变量的系统的解：
这里 Wolfram 语言使用 CAD 找到带有三个变量的原始系统的解：

LinearQE

LinearQE 选项设定处理下述系统的方法：系统至少含有一个最内层的量词变量，而这种变量在系统的所有方程和不等式中的出现至多是线性的. 该选项的设置对于决策问题的求解无影响. 在默认设置 True 时，Wolfram 语言使用 Loos–Weispfenning 算法 [15] 来消去所有在系统中只以线性形式出现的量词变量，随后若有剩下的量词，或是需要对自由变量解出结果，CAD 算法将被采用. 设置 LinearQE->Automatic，使得 Loos–Weispfenning 算法只用于线性并带有常数系数的变量. 设置 LinearQE->False 使得 Loos–Weispfenning 算法不被采用.

默认设置 LinearQE->True 使 Loos–Weispfenning 算法被用于消去 和 ，然后用 CAD 算法求解余下的带有两个变量的无量词系统：
设置 LinearQE->Automatic，使 Loos–Weispfenning 算法只用于对 的消去，对于 余下的带有三个变量的无量词系统的求解则用 CAD 算法. 对于这个例子，默认算法快很多：
设置 LinearQE->False，使 Loos–Weispfenning 算法不被使用. Reduce 使用 CAD 对带有四个变量的原始系统求解. 在这个例子中，这种方法需要很长的时间：
三种方法的答案相同：
下面这个例子中默认方法不是最快的方法. 默认设置的 LinearQE->True 使 Loos–Weispfenning 算法被用于消去 和 ，对于余下的带有一个量化变量和一个自由变量的系统则用 CAD 算法：
设置 LinearQE->Automatic，使 Loos–Weispfenning 算法只用与对 的消去，对于余下的带有两个量化变量和一个自由变量的系统则用 CAD 算法：
设置 LinearQE->False 使 CAD 算法用于这个系统的求解. 这是求解该例子的最快的方法：
对于量词消去问题，如果所有的量化变量在系统中仅为线性，并且系统的无量词版本不必以解出形式给出，默认设置 LinearQE->True 无疑是最优秀的. 这是因为 Loos–Weispfenning 算法的复杂性几乎与自由变量的数目无关. 这一点与 CAD 算法不同，CAD 算法的复杂性是自由变量的数目的双重指数函数（doubly exponential）. 设置为 LinearQE->False 且 QuadraticQE->False 时，这个例子无法在1000秒内完成：

LWPreprocessor

选项 LWPreprocessor 的设置影响决策问题的求解和解的实例的寻找. 该选项用于设定是否采先用 Loos–Weispfenning 算法 [8] 来消去在所有方程和不等式中至多是线性的变量，再对所得系统应用 CAD 算法. 默认设置为 Automatic，这种设置时 Wolfram 语言使用 Loos–Weispfenning 算法来消去只以线性形式存在且带有常数系数的变量. 设置为 LWPreprocessor->True 时，Loos–Weispfenning 算法用于只以线性形式存在的所有变量. 设置为 LWPreprocessor->False 时，Loos–Weispfenning 算法不用作基于 CAD 决策算法的预处理器.

缺省设置 LWPreprocessor->Automatic 使 Loos–Weispfenning 算法只用于对 的消去，对于余下的带有三个变量的系统，将用 CAD 求解：
设置 LWPreprocessor->True 使 Loos–Weispfenning 算法用于消去 和 ，对于余下的带有两个变量的系统，将用 CAD 求解. 对于这个例子，这种方法比默认方法慢：
设置为 LWPreprocessor->False 时，CAD 算法被用来对带有四个变量的原始系统求解. 在这个例子中，这种方法与默认方法一样快：
下面这个例子与上述例子的不同之处仅在于：最后一个不等式变成了一个方程. 默认设置 LWPreprocessor->Automatic 使 Loos–Weispfenning 只用于消去，CAD 算法被用来对带有三个变量的剩余系统求解：
设置 LWPreprocessor->True 使 Loos–Weispfenning 算法用来消去 和 ，对于余下的带有两个变量的系统，将用 CAD 求解. 对于这个修改了的例子，采用这个方法比默认方法快：
设置 LWPreprocessor->False 使得 CAD 算法被用于对带有四个变量的原始系统的求解. 对于这个修改了的例子，采用这个方法比默认方法慢了七倍：

ProjectAlgebraic

选项 ProjectAlgebraic 的设置影响 CAD 算法中对代数数值系数的处置.

在输入系统的系数中出现的代数数被新的变量代替. 在进行变量排序时，新的变量总是放在首位，这样在 CAD 算法的投影阶段，这些变量将被最后消去. 当当前的投影多项式包含 个变量，并且至少头 个变量用来代替代数数系数时，可以对是否继续投影阶段进行选择. 如果不继续投影阶段，可以开始提升阶段，在每一个变量都与对应的代数数系数相等的头 个变量中延展零维单元. 如果选择的是要计算最后 个投影，那么在提升阶段中我们可能会发现，与所提升的一个变量相对应的代数数系数在投影多项式的根之间. 进而对于这个变量，我们将要延展一个带有一个有理数采样点的一维单元. 因此用户要在避免计算最后 个投影和避免采样点的代数数坐标两者之间作出折衷的选择.

设置为 ProjectAlgebraic->True 时，对代替代数数系数的变量的投影阶段继续进行，直到只剩一个变量为止. 设置为 ProjectAlgebraic->False 时，一旦剩下一个不代替代数数系数的变量时，投影阶段即被终止. 采用默认设置 ProjectAlgebraic->Automatic 时，当至多只剩一个不替代代数数系数的变量且至少存在三个投影多项式，或者是存在一个投影变量次数大于二的投影多项式时，投影阶段终止.

对于方程和不等式的数目很少、且高次代数数系数的数目也很少的系统，ProjectAlgebraics->True 往往是一个较好的选择. （输出中使用 N 是为了更好的可读性.）
对于带有许多低次代数数系数、方程和不等式的系统，ProjectAlgebraics->False 往往速度较快：

ProveMultiplicities

设置 ProveMultiplicities 用于确定 CAD 算法在提升阶段验证通过任意精度浮点数（Wolfram 语言 "bignum"）计算得到的投影多项式的多重根和零首系数的方法（详情请参见 [14, 24]）. 默认设置ProveMultiplicities->True 时，Wolfram 语言利用单元原点的信息，如果没有足够的信息，则计算单元坐标的准确值，并且使用主子结式系数和精确零测试，只有在这个方法失败的情况下才转为精确计算. 设置 ProveMultiplicities->Automatic 使 Wolfram 语言采用单元原点的信息，如果信息量不够，则转为精确计算. 设置 ProveMultiplicities->False 使 Wolfram 语言在每一次任意精度（bignum）计算不能将所有根分离，或者不能证实投影多项式的首系数非零时，转为精确计算.

一般而言，使用全部现有的验证由任意精度浮点数计算得到的结果的方法，会有更好的效果：

QuadraticQE

选项 QuadraticQE 设定是否使用 Weispfenning 虚拟替代算法的量词消去的二次情形 [22, 23] 对系统的所有方程和不等式中最多为二次的量化变量进行消去. Weispfenning 算法的复杂性与自由变量的数目几乎无关，这一点与 CAD 算法不同，CAD 算法的复杂性是所有变量的数目的双指数函数（doubly exponential）. 因此，当所有量词均可用这种方法消去，有许多自由变量存在，以及系统的无量词版本无需用解出形式给出时，这种方法的优越性是毋庸置疑的. 而另一方面，使用 Weispfenning 算法消去变量常常显著增加公式的大小. 因此，如果 Wolfram 语言需要在结果中应用 CAD，或是系统中的自由变量很少，在原始系统中使用 CAD 可能较快. 在默认设置 Automatic 下， 在没有指明变量及至少出现两个参数的情况时，对于 Resolve，Wolfram 语言使用这种算法；对于 Reduce 和 Resolve，对于至少有三个变量的情形，只要一个变量的消除至多使系统的 LeafCount 增倍，Wolfram 语言在默认设置 Automatic 下，也使用这种算法. 这个判据看起来运行良好，然而对于某些情形它不能对算法作出最优化的选择. 对选项值进行改变可以使某些原本要花费很长时间的问题得到较快地解决. 在设置为 QuadraticQE->True 时, 只要有一个二次变量要消去，就使用 Weispfenning 算法，而设置为 QuardaticQE->False，Weispfenning 算法将不被采用.

Resolve 在没有指明变量，且至少出现两个参数时使用 Weispfenning 算法来消去 . 所得结果对参数 、 和 为未解出形式：
在该例中，Reduce 默认情况下使用 CAD 算法. 结果对于参数 、 和 是解出的：
设置为 QuadraticQE->True 时，Reduce 使用 Weispfenning 算法来消去 ，然后使用CAD 解出关于参数 、 和 的无量词公式. 在这个例子中，使用这种方法比从一开始就使用默认的 CAD 算法要快：
对于这个含有三个自由变量的系统，Weispfenning 算法要比 CAD 算法快得多：
对于这个只有一个自由变量的系统，Resolve 采用 CAD：
Weispfenning 算法用的时间较长，并且给出的结果较复杂：

QVSPreprocessor

选项 QVSPreprocessor 的设置影响着决策问题的解决和解得实例的寻找. 该选项设定是否先使用虚拟替代算法 [22, 23] 的 Weispfenning 量词消去的二次情形来消去在所有方程和不等式中至多以二次形式出现的变量，随后在所得到的系统中应用 CAD 算法. 默认设置为 False，此时该算法不被使用. 对有些例子中，使用 Weispfenning 算法作为预处理显会著改善了运行效果，而对另一些例子，使用这种预处理则会严重损害运行效果. 对于变量很多且有解的实例存在时，这种预处理似乎会起到帮助作用. 设置为 QVSPreprocessor->True 时，每当存在二次变量，Weispfenning 算法就被采用. 设置为QVSPreprocessor->Automatic 时，Wolfram 语言对于至少有四个变量的系统才使用这种算法.

这里 Wolfram 语言使用Weispfenning 算法作为预处理得到了解. 如果不用这种预处理，这个例子将用更多时间：
对于这个例子，使用无预处理的 CAD 算法较快：

ReducePowers

对于 CAD 算法输入中的任意变量 ，如果系统中 的幂是另外一个整数 的整数倍，Wolfram 语言将在输入系统中用一个新的变量来取代 ，在新的系统中运行 CAD，然后对结果求解以将解以原始变量的形式表示. 设置ReducePowers->False 关闭这种快捷方式. 设置为 ReducePowers->False 时， 在 CAD 算法的输出中以单元界限（cell bound）出现的代数函数必须是有理函数、二次根表达式或 Root 对象. 在默认设置 ReducePowers->True 时，它们还有可能是 ，其中 为任何前面出现的表达式；或者是 Root[a#n-e&,1]，其中 是某个整数， 是一个有理函数或是一个二次根表达式.

默认设置 ReducePowers->True 时，CAD 算法求解关于替代 和 的变量的一个二次方程，然后将结果以 和 的形式表示. 该结果包含内部包含二次根表达式的 Root 对象：
设置为 ReducePowers->True 时，CAD 算法用几倍长的时间求解原始的50次方程. 结果仅包含内部为多项式的 Root 对象：

RootReduced

对于带有等式约束，且该约束形成一个零维理想 的系统，Wolfram 语言使用 CAD 算法的一种变形，用 Gröbner 基的方法来得到投影多项式. 如果 的字典序 Gröbner 基包含线性多项式，并且这些多项式中，除了最后一个变量外的其它变量的系数都为常数（这也正是“通常”的情况），则解的所有坐标都可以很容易用最后一个坐标的多项式形式表示出来. 否则，坐标以表示三角方程组定义的代数数的 Root 对象的形式给出. 将 RootReduced 设为 True，导致 Wolfram 语言用由最小多项式和根数定义的单一数值 Root 对象来表示每一个坐标. 计算这种化简后的表示往往比直接对系统求解要花费更长的时间.

默认设置下， 的值以 的形式表示出来：
当设置为 Backsubstitution->True，我们得到了以 AlgebraicNumber 表示的 的数字值：
设置 RootReduced->True 使 Wolfram 语言用单一 Root 对象的形式来表示 的值. 然而这种计算要花费相当长的时间：
默认情况下，Reduce 以 Root 对象的形式表示解，代表由三角方程组定义的代数数：
设置 RootReduced->True 使得 Wolfram 语言用由最小多项式和根数定义的 Root 对象的形式表示 . 但计算需要的时间较长：

SimplifyInequalities

在默认设置 SimplifyInequalities->Automatic 时，Wolfram 语言使用[25] 中提出的不等式简化启发式，简化 CAD 算法的输入，推断 CAD 投影因子的不等式，使用不等式识别非零系数和投影阶段的子生成物，并消除提升阶段的单元. 启发式也用于简化虚拟替换算法的中间结果[15, 23]. 将 SimplifyInequalities 设置为 True 使得不等式简化启发式执行额外的变换 . 在设置 SimplifyInequalities->False 下，不使用不等式简化启发式.

在这个例子中，不等式简化使得 CAD 计算变快：
在第一个方程示例中，因式分解使得 CAD 计算变快；在第二个示例中，它使得 CAD 计算变慢：

ThreadOr

选项 ThreadOr 设定恒等式

如何在决策算法（对于无自由变量或参数的系统，为 Reduce 和 Resolve）、FindInstance 和量词消去（未指定变量时，为 Resolve）中被使用. 默认设置 ThreadOr->True 时，恒等式（8）在尝试任何算法前被使用. 设置为 ThreadOr->False 时，恒等式（8）被要求使用它的算法使用（例如 Simplex 算法），但如果算法不要求使用则不被使用（例如 CAD 算法）.

这里 Reduce 找到了一个满足 Or 的较简单的第一项的一个实例，这样就避免了应对更复杂的第二项：
设置为 ThreadOr->False 时，Reduce 需要对整个系统运行一个基于 CAD 的决策算法：
该系统无解，因此在设置为 ThreadOr->True 时，Reduce 需要对每一项运行一个基于 CAD 的决策算法：
由于 Or 的所有六个项都涉及到完全相同的多项式，对整个表达式运行基于 CAD 的决策算法与对其中一项运行基于 CAD 的决策算法的计算非常相似. 在这个例子中设置 ThreadOr->False 时，计算速度较快：

ZengDecision

选项 ZengDecision 指定 Wolfram 语言是否使用 G. X. Zeng 和 X. N. Zeng [18] 的算法. 该算法适用于由单一严格不等式（single strict inequality）组成的系统的决策问题. 与 [13] 中描述的 CAD 算法的严格不等式变体相比，有一些例子证明该算法的效果较好. 然而，对于随机选择的不等式，其效果较差；因此默认情况下不用该算法. 这是一个[18] 中的例子，使用设置 ZengDecision->True 使运行速度稍快：

参考文献

[1] Caviness B. F. and J. R. Johnson, eds. Quantifier Elimination and Cylindrical Algebraic Decomposition: Texts and Monographs in Symbolic Computation. Springer-Verlag (1998)
[2] Tarski A. A Decision Method for Elementary Algebra and Geometry. University of California Press (1951)
[3] Łojasiewicz S. Ensembles Semi-Analytiques. Inst. Hautes Études Sci. (1964)
[4] Collins G. E. "Quantifier Elimination for the Elementary Theory of Real Closed Fields by Cylindrical Algebraic Decomposition" Lecture Notes in Computer Science 33 (1975): 134–183
[5] Hong H. "An Improvement of the Projection Operator in Cylindrical Algebraic Decomposition" In Issac ’90: Proceedings of the International Symposium on Symbolic and Algebraic Computation (M. Nagata, ed.), 261–264, 1990
[6] McCallum S. "An Improved Projection for Cylindrical Algebraic Decomposition of Three Dimensional Space" J. Symb. Comput. 5, no. 1/2 (1988): 141–161
[7] McCallum S. "An Improved Projection for Cylindrical Algebraic Decomposition" In Quantifier Elimination and Cylindrical Algebraic Decomposition: Texts and Monographs in Symbolic Computation (B. F. Caviness and J. R. Johnson, eds.). Springer-Verlag, 242–268, 1998
[8] Brown C. W. "Improved Projection for Cylindrical Algebraic Decomposition" J. Symb. Comput. 32, no. 5 (2001): 447–465
[9] Collins G. E. "Quantifier Elimination by Cylindrical Algebraic Decomposition—Twenty Years of Progress" In Quantifier Elimination and Cylindrical Algebraic Decomposition: Texts and Monographs in Symbolic Computation (B. F. Caviness and J. R. Johnson, eds.). Springer-Verlag, 8–23, 1998
[10] McCallum S. "On Projection in CAD-Based Quantifier Elimination with Equational Constraint" In Issac ’99: Proceedings of the International Symposium on Symbolic and Algebraic Computation (Sam Dooley, ed.), 145–149, 1999
[11] McCallum S. "On Propagation of Equational Constraints in CAD-Based Quantifier Elimination" In Issac 2001: Proceedings of the International Symposium on Symbolic and Algebraic Computation, 223–231, 2001
[12] Strzebonski A. "An Algorithm for Systems of Strong Polynomial Inequalities" The Mathematica Journal 4, no. 4 (1994): 74–77
[13] Strzebonski A. "Solving Systems of Strict Polynomial Inequalities" J. Symb. Comput. 29, no. 3 (2000): 471–480
[14] Strzebonski A. "Cylindrical Algebraic Decomposition Using Validated Numerics" Paper presented at the ACA 2002 Session on Symbolic-Numerical Methods in Computational Science, Volos, Greece (2002) (Notebook with the conference talk available at members.wolfram.com/adams)
[15] Loos R. and V. Weispfenning. "Applying Linear Quantifier Elimination" Comput. J. 36, no. 5 (1993): 450–461
[16] Strzebonski A. "A Real Polynomial Decision Algorithm Using Arbitrary-Precision Floating Point Arithmetic" Reliable Comput. 5, no. 3 (1999): 337–346; Developments in Reliable Computing (Tibor Csendes, ed.). Kluwer Academic Publishers (1999): 337–346
[17] Aubry P., F. Rouillier, and M. Safey El Din. "Real Solving for Positive Dimensional Systems" J. Symb. Comput. 34, no. 6 (2002): 543–560
[18] Zeng G. X. and X. N. Zeng. "An Effective Decision Method for Semidefinite Polynomials" J. Symb. Comput. 37, no. 1 (2004): 83–99
[19] Akritas A. G. and A. Strzebonski. "A Comparative Study of Two Real Root Isolation Methods" Nonlinear Analysis: Modelling and Control 10, no. 4 (2005): 297–304
[20] Faugere J. C., P. Gianni, D. Lazard, and T. Mora. "Efficient Computation of Zero-Dimensional Gröbner Bases by Change of Ordering" J. Symb. Comput. 16, no. 4 (1993): 329–344
[21] Dorato P., W. Yang, and C. Abdallah. "Robust Multi-Objective Feedback Design by Quantifier Elimination" J. Symb. Comput. 24, no. 2 (1997): 153–159
[22] Weispfenning V. "Quantifier Elimination for Real Algebra—The Cubic Case" In Issac 1994: Proceedings of the International Symposium on Symbolic and Algebraic Computation, 258–263, 1994
[23] Weispfenning V. "Quantifier Elimination for Real Algebra—The Quadratic Case and Beyond" Appl. Algebra Eng. Commun. Comput. 8, no. 2 (1997): 85–101
[24] Strzebonski A. "Cylindrical Algebraic Decomposition Using Validated Numerics" J. Symb. Comput. 41, no. 9 (2006): 1021–1038
[25] Brown C. W. and A. Strzebonski. "Black-Box/White-Box Simplification and Applications to Quantifier Elimination" In Issac 2010: Proceedings of the International Symposium on Symbolic and Algebraic Computation (Stephen M. Watt, ed.), 69–76, 2010
[26] Strzebonski A. "Computation with Semialgebraic Sets Represented by Cylindrical Algebraic Formulas" In Issac 2010: Proceedings of the International Symposium on Symbolic and Algebraic Computation (Stephen M. Watt, ed.), 61–68, 2010
[27] Strzebonski A. "Solving Polynomial Systems over Semialgebraic Sets Represented by Cylindrical Algebraic Formulas" In Issac 2012: Proceedings of the International Symposium on Symbolic and Algebraic Computation (Joris van der Hoeven and Mark van Hoeij, eds.), 335–342, 2012
[28] Strzebonski A. "Cylindrical Algebraic Decomposition Using Local Projections" In Issac 2014: Proceedings of the International Symposium on Symbolic and Algebraic Computation (Katsusuke Nabeshima, ed.), 389–396, 2014