WXF Format Description

WXF is a binary format for faithfully serializing Wolfram Language expressions in a form suitable for outside storage or interchange with other programs. WXF can readily be interpreted using low-level native types available in many programming languages, making it suitable as a format for reading and writing Wolfram Language expressions in other programming languages.

The basic functions for converting between a Wolfram Language expression and its serialized form are BinarySerialize and BinaryDeserialize. Support for reading and writing files with WXF data is built into Export and Import.

BinarySerialize[expr]	gives a binary representation of any expression expr in the WXF format
BinaryDeserialize[bytearray]	recovers an expression from a binary representation in the WXF format
Import[file,"WXF"]	imports a WXF file and returns an expression
Export[file,expr,"WXF"]	serializes an arbitrary expression and saves it as a WXF file
ImportByteArray[ba,"WXF"]	imports data and returns an expression
ExportByteArray[expr,"WXF"]	generates a ByteArray object corresponding to expr exported in the WXF format

There are many ways to serialize and deserialize WXF in the Wolfram Language.

Basic Structure

Data in WXF form always contains a plain ASCII header followed by a string of bytes. The header specifies how the bytes can be decoded and is separated by a colon from the string of bytes that represents a sequence of parts.

The byte array continues by giving a sequence of parts, each starting with a token from the following list that specifies the type of the part.

byte value	character representation (ISO8859-1)	type of part
102	"f"	function
67	"C"	signed 8-bit integer
106	"j"	signed 16-bit integer
105	"i"	signed 32-bit integer
76	"L"	signed 64-bit integer
114	"r"	IEEE double-precision real
83	"S"	string
66	"B"	binary string
115	"s"	symbol
73	"I"	big integer
82	"R"	big real
193	"Á"	packed array
194	"Â"	numeric array
65	"A"	association
58	":"	delayed rule in association
45	"-"	rule in association

The exhaustive list of WXF tokens.

After the token comes, if necessary, a length specification, followed by the sequence of actual content elements for the part.

Basic Examples

Give the bytes for the serialized form of a symbol:

View the bytes as characters in "ISO8859-1":

Give the bytes for the serialized form of a string as characters:

Give the bytes for the serialized form of Range[10]:

Create a function to label pieces of the array:

The first two bytes belong to the header, the rest corresponds to the packed array:

The header with the version followed by the separator:

The packed array with the type, the rank and dimensions, and finally the data:

Examples with Multiple Parts

The examples in the previous section essentially consisted of a single part. There was a single token from the token list, followed by size information, followed by the data. The examples in this section contain multiple parts and types. The first example is shown by the following interactive illustration:

The first two bytes are the header and colon separator:

The next byte is the token for a function, followed by the number of arguments:

The next byte is the token of the function's head, in this case symbol:

After that is the number of bytes in the UTF-8 representation of the symbol:

Therefore, the next 6 bytes are the UTF-8 representation of the symbol:

The complete head being read, the next byte is the token of the first argument:

As this argument is a symbol, the next byte will be its length, followed by its name:

The function only had one argument, so all the bytes must be read by now:

The second example is a list of three elements. The list is represented as a function of length 3, with head List followed by three parts. The first parts introduce the format used to represent integers in a compact form using a token and an "Integer8". The last part shows the representation of a ByteArray:

Give the bytes for the serialized form of {1,-1,ByteArray[{1,2,3}]}:

Ignoring the header, this expression is a function of three arguments:

The head is a symbol of four bytes, namely List:

After the head comes the first argument, namely the 8-bit integer 1:

The next two bytes are the second argument, namely the 8-bit integer -1:

Use Mod to interpret the byte as a signed value, converting 255 to the expected -1:

The third and final argument is a binary string of length 3 with values {1,2,3}:

More on the Header

The header is a plain ASCII string of variable length, delimited by the character ":". For the current version (1.0) of WXF, the first byte in the header is the character "8" (i.e. byte value 56). When the binary serialization is zip compressed, this is indicated in the header by the character "C". The header is never compressed; the compression only applies to the following string of bytes.

Serialize an expression to give a byte array:

The first byte is the character 8:

Compression is indicated by the second character of the header being "C":

Length Encoding (Varint)

WXF types fall into three categories:

Atomic types of fixed length like machine-precision Integer or Real.

Atomic types of variable length like String or Symbol.

Types with a variable number of subparts like general expressions (token type "f" for function) or Association.

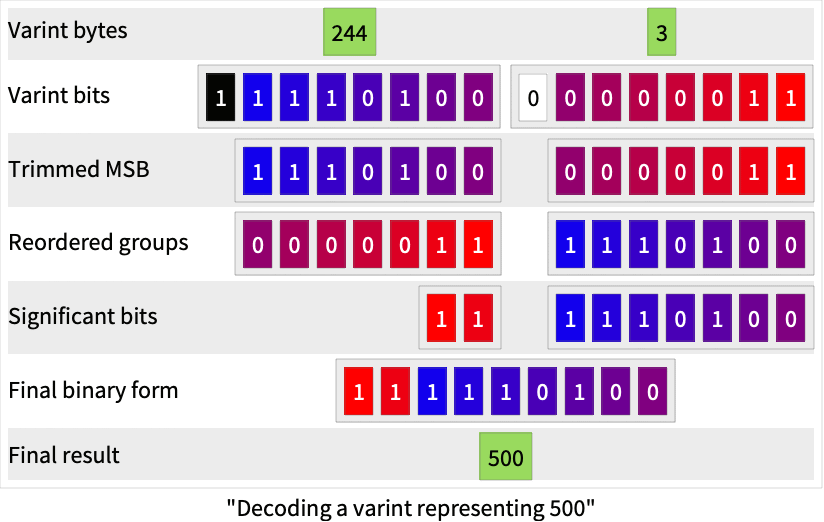
In WXF, all integers representing a length or a size are serialized using the varint method. A varint is a self-indicating variable-length format, where smaller integers require fewer bytes. Each byte except the last one has its most significant bit (MSB) set. The MSB indicates if the following byte of the stream is also part of the varint, acting as a continuation marker. The lower seven bits of each byte store the binary representation of the integer, with the least significant group first.

Here is an example of constructing the varint representation of 500:

Base-2 digits of 500:

Group bits by 7, with the least significant bits first:

Order bits of each group, with the most significant bit first, and pad each group so that they have 8 bits each:

Set the first bit of each byte except the last one to get the varint binary form:

Construct byte values from base-2 digits, to give the varint representation of 500:

The reverse operation of decoding the varint encoded byte sequence {244,3} back to 500 is explained in the following illustration, in which each initial varint bit is assigned a unique color:

Strings, Symbols and Non-Machine Numbers

Strings, symbols and non-machine numbers are represented using the same format. The first byte is a token, then the byte count encoded in the varint format, followed by a string of Unicode characters encoded as UTF-8 corresponding to the string InputForm of the expression. A non-machine number can be either an arbitrary-precision real or an integer that requires more than $SystemWordLength bits to represent.

type of atom	token	representation
String	"S"	the Unicode character sequence
Symbol	"s"	the fully qualified name of the symbol, specifying the context, except for System` symbols
Arbitrary-precision reals	"R"	the digit representation specifying the mantissa and eventually the precision and the exponent
Big integers	"I"	the string of digits

Types based on InputForm.

Serialize the first 500 characters of Alice in Wonderland:

The first byte after the header is the token for a string:

The next two bytes are 500 in the varint encoding as seen in the preceding example:

The remaining bytes are the string contents in UTF-8:

Serialize a non-machine integer:

Other than the token, the serialization is the same as for a string:

A number with one fewer digit requires only a single byte to encode the length:

Machine Integers Serialization

Machine integers are identified by the smallest integer type from the following list that can represent the value, followed by the two's complement representation of the integer. The byte ordering is always little endian.

token	definition	type size
"C"	signed 8-bit integer
"j"	signed 16-bit integer
"i"	signed 32-bit integer
"L"	signed 64-bit integer

Integer tokens, their associated types and the number of bytes used by each representation.

The bytes corresponding to the serialization of 2^14:

Skip the two-byte header and display the first token as a character:

View the bytes after the token:

Convert the preceding pair of bytes to an integer:

Negative integers binary representation uses the two's complement method. Given a N-bit integer α, its two's complement β is its complement with respect to 2^N: α+β=2^N. Negation of a number is performed by taking the two's complement.

The two's complement of the 8-bit integer 1:

The two's complement is the 8-bit binary representation of -1:

Serialize a negative 16-bit integer:

The last two bytes are the integer value:

Convert the pair of bytes to its decimal form:

The value is the 16-bit two's complement of 10000:

Machine Reals Serialization

Machine reals are represented using the character "r" followed by the memory representation of a double floating-point value in the IEEE 754 standard. As for machine integers, the byte ordering is always little endian.

Serialize a real number:

Skip the two-byte header and display the first token as a byte and as a character:

The next bytes are the real value in the IEEE 754 standard:

Machine-precision complex numbers are serialized as a function of two machine-precision reals. The following illustration highlights the Complex head followed by two real values:

Serialize a machine complex number:

The first bytes after the header are a function of length 2 with head Complex:

The next nine bytes are the real part and match the serialization of the real value 4. as shown in the previous example:

The remaining bytes are the imaginary part, again the real value 4.:

Function Serialization

Functions are represented in WXF by the character "f", followed by the expression length in the varint format. The number of elements is equal to the length incremented by one, for the head. The head and the parts are arbitrary serialized expressions. In particular, the head can also be a function: Select[OddQ][{1,2,3}] is a function of length 1 with head Select[OddQ], which itself is a function with head Select and length 1.

Serialize an expression, using Unevaluated to prevent it from evaluating:

The first two bytes correspond to a function of length 1:

The next 16 bytes are the serialization of the head Select[OddQ] shown previously:

The remaining bytes are the argument, with the token and length first:

Followed by the head:

The three machine integers round out the expression:

Associations Serialization

Associations are represented by the character "A", followed by the length and the rules.

An association's rules are represented by the character "-", and delayed rules by the character ":". It is immediately followed by two arbitrary serialized expressions. The length of the association's rule is always two and thus is omitted. The following illustration shows the serialization of a simple association:

Serialize the association:

The first bytes correspond to an association of two elements:

Then comes the rule that implicitly has two parts; the length is thus omitted:

The delayed rule is the final part:

Rules of the previous example were part of an association. Rule and RuleDelayed that are not part of an Association are serialized as functions. The serialized form is less packed, as shown in the next example.

Serialize a list of rules:

The first bytes declare a list of two elements:

The first element is a function of length 2 with head Rule:

The rule's arguments remain the same as in the association case:

The second element is also a function of length 2, but its head is RuleDelayed:

Similarly, the elements of the rule delayed remain unchanged:

The serialized length is roughly the size of the string FullForm:

The association serializes to a more compact form:

Binary Strings

Binary strings are represented by the token "B". They follow the same pattern as strings, but the byte sequence is arbitrary rather than UTF-8 characters. A ByteArray is serialized as a binary string.

Serialize a byte array:

The first byte after the header is a binary string token, followed by the length of the binary data:

The next bytes are the data:

Decoding the bytes as UTF-8 does not always succeed:

The bytes can always be represented as a string using the "ISO8859-1" encoding:

Numeric Arrays

Arrays are multidimensional tables of machine-precision numeric values. Arrays are represented by the following sequence: a token specifying the type of array, a token specifying the type of the values, the rank in the varint format, the dimensions as a sequence of integers also in the varint format and finally, the data.

There are two types of arrays in the WXF format: packed arrays represented by the token "Á" (byte value 193) and numeric arrays represented by the token "Â" (byte value 194). There are slight differences between the two, the major one being the supported value type, as described in the following tables.

integer value	value in hexadecimal representation	type of array
0	00₁₆	array of 8-bit signed integers
1	01₁₆	array of 16-bit signed integers
2	02₁₆	array of 32-bit signed integers
3	03₁₆	array of 64-bit signed integers (64-bit system only)
34	22₁₆	array of IEEE single-precision real numbers (float)
35	23₁₆	array of IEEE double-precision real numbers (double)
51	33₁₆	array of IEEE single-precision complex numbers
52	34₁₆	array of IEEE double-precision complex numbers

The valid value type tokens for packed arrays.

integer value	value in hexadecimal representation	type of array
0	00₁₆	array of 8-bit signed integers
16	10₁₆	array of 8-bit unsigned integers
1	01₁₆	array of 16-bit signed integers
17	11₁₆	array of 16-bit unsigned integers
2	02₁₆	array of 32-bit signed integers
18	12₁₆	array of 32-bit unsigned integers
3	03₁₆	array of 64-bit signed integers
19	13₁₆	array of 64-bit unsigned integers
34	22₁₆	array of IEEE single-precision real numbers (float)
35	23₁₆	array of IEEE double-precision real numbers (double)
50	33₁₆	array of IEEE single-precision complex numbers
51	34₁₆	array of IEEE double-precision complex numbers

The valid value type tokens for numeric arrays.

The integer range supported by packed arrays varies with the system word length, $SystemWordLength, from -2³¹ to 2³¹-1 on a 32-bit environment, and from -2⁶³ to 2⁶³-1 on a 64-bit environment.

Define a matrix:

Serialize it as a packed array:

The first byte after the header is the packed array token:

The next byte indicates an array of 16-bit signed integers:

The following bytes are the rank and dimensions of the array:

The trailing bytes are the values:

It is possible to reconstruct the decimal form of each 16-bit integer. First, group the pair of bytes:

Each pair is a little endian 16-bit long integer whose value is reconstructed using a bit shift operation:

The interactive illustration following shows the serialization of the previous matrix before packing. The sequence of elements is significantly different, since it involves nested functions with head List. The inner lists have three parts corresponding to the integer values. It is worth noting that the binary representation of the integer values is similar to the one witnessed in the packed array case (little endian signed 16-bit integer).

Array value type tokens are constructed as bit fields. The four least significant bits store the log of the size of the numeric type in bytes, and the four most significant bits represent the numeric type. Note that for complex types, the size refers to the whole number, so that, for example, the single-precision complex type is considered to have a size of 8 bytes.

0000
0001
0010
0011
0100

The four least significant bits of the value type token and the corresponding type sizes in bytes.

0000	integer
0001	unsigned integer
0010	real
0011	complex

The four most significant bits of the value type token and the corresponding numeric types.

It is possible to construct the bit field corresponding to an array of double-precision reals using the Wolfram Language.

A double-precision real is 8 bytes long; the logarithm to base 2 is 3:

Find the bit representation:

View the bit field made from the concatenation of the numeric type corresponding to a real number and the type size:

Convert the preceding bit sequence to retrieve the expected byte value:

Top