WOLFRAM

Wolfram Language & System Documentation Center

AlgebraicNumberNorm[a]

gives the norm of the algebraic number a.

Details and Options
Details and Options Details and Options
Examples  
Basic Examples  
Scope  
Options  
Extension  
Applications  
Properties & Relations  
Neat Examples  
See Also
Tech Notes
Related Guides
History
Cite this Page

AlgebraicNumberNorm

AlgebraicNumberNorm[a]

gives the norm of the algebraic number a.

Details and Options

  • The norm of a is defined to be the product of the roots of its minimal polynomial.
  • AlgebraicNumberNorm[a,Extension->θ] finds the norm of a over the field .

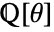Examples

open all close all

Basic Examples  (1)

Norms of algebraic numbers:

Scope  (4)

Integers and rational numbers:

Radical expressions:

Root and AlgebraicNumber objects:

AlgebraicNumberNorm automatically threads over lists:

Options  (1)

Extension  (1)

Norm of over :

Applications  (1)

is irreducible in :

Since AlgebraicNumberNorm is multiplicative, having a prime norm implies the original number is prime:

Properties & Relations  (3)

AlgebraicNumberNorm is multiplicative:

Units in a number field have norm :

Compute the smallest field that includes , i.e. :

Compute the norm in that field:

Neat Examples  (1)

Plot of norms of elements in :

Wolfram Research (2007), AlgebraicNumberNorm, Wolfram Language function, https://reference.wolfram.com/language/ref/AlgebraicNumberNorm.html.

Text

Wolfram Research (2007), AlgebraicNumberNorm, Wolfram Language function, https://reference.wolfram.com/language/ref/AlgebraicNumberNorm.html.

CMS

Wolfram Language. 2007. "AlgebraicNumberNorm." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AlgebraicNumberNorm.html.

APA

Wolfram Language. (2007). AlgebraicNumberNorm. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AlgebraicNumberNorm.html

BibTeX

@misc{reference.wolfram_2025_algebraicnumbernorm, author="Wolfram Research", title="{AlgebraicNumberNorm}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/AlgebraicNumberNorm.html}", note=[Accessed: 08-August-2025]}

BibLaTeX

@online{reference.wolfram_2025_algebraicnumbernorm, organization={Wolfram Research}, title={AlgebraicNumberNorm}, year={2007}, url={https://reference.wolfram.com/language/ref/AlgebraicNumberNorm.html}, note=[Accessed: 08-August-2025]}