Wolfram Mathematica Documentation Center
DOCUMENTATION CENTER SEARCH
New to Mathematica? Find your learning path »
Mathematica > Mathematics and Algorithms > Matrices and Linear Algebra > Matrix Operations > ConjugateTranspose >
Mathematica > Mathematics and Algorithms > Graphs & Networks > Graph Programming > Matrices and Linear Algebra > Matrix Operations > ConjugateTranspose >
Mathematica > Visualization and Graphics > Graphs & Networks > Graph Programming > Matrices and Linear Algebra > Matrix Operations > ConjugateTranspose >
BUILT-IN MATHEMATICA SYMBOLTutorials »|See Also »|More About »

ConjugateTranspose

ConjugateTranspose[m]
or gives the conjugate transpose of .
MORE INFORMATION
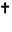  • can be entered as Esc ct Esc or \[ConjugateTranspose].
  • ConjugateTranspose[m] can also be given as 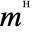, where 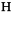can be entered as Esc hc Esc or \[HermitianConjugate].
EXAMPLESCLOSE ALL
Basic Examples   (2)
Conjugate transpose of a complex-valued matrix:
Enter using Esc ct Esc:
Conjugate transpose of a complex-valued matrix:
In[1]:=
Click for copyable input
In[2]:=
Click for copyable input
Out[2]//MatrixForm=
In[3]:=
Click for copyable input
Out[3]//MatrixForm=
 
Enter using Esc ct Esc:
In[1]:=
Click for copyable input
Out[1]=
Scope   (2)
Conjugate transpose a sparse array:
The conjugate transpose is sparse:
ConjugateTranspose works for symbolic matrices:
ComplexExpand assumes all variables are real:
Generalizations & Extensions   (1)
ConjugateTranspose works similarly to Transpose for tensors:
Conjugate and transpose the first two dimensions:
Conjugate and transpose the first and third dimensions:
Applications   (1)
is a random complex matrix:
Find the QRDecomposition of :
is unitary, so its inverse is
Reconstruct from the decomposition:
Properties & Relations   (2)
ConjugateTranspose[m] is equivalent to Conjugate[Transpose[m]]:
The product of a matrix and its conjugate transpose is Hermitian:
is the matrix product of and .
so is Hermitian:
New in 5.1
Ask a question about this page  |  Suggest an improvement  |  Leave a message for the team
Format:   HTML  |  CDF