Disjunction
Disjunction[expr,{a1,a2,…}]
gives the disjunction of expr over all choices of the Boolean variables ai.
Details
- Disjunction[expr,{a1,a2,…}] applies Or to the results of substituting all possible combinations of True and False for the ai in expr.
- Disjunction gives a resolved form of
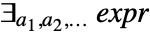. - Disjunction is to Or what Sum is to Plus.
Examples
open all close allBasic Examples (3)
Properties & Relations (5)
Disjunction effectively computes the Or over all truth values of the listed variables:
Disjunction is typically more efficient and can work large numbers of variables:
Disjunction eliminates ∃ (Exists) quantifiers for the list of variables:
Use Resolve to eliminate more general combinations of quantifiers:
SatisfiableQ is Disjunction over all variables:
Use Conjunction to compute And over a list of variables:
Conjunction is related to Disjunction by de Morgan's law:
Disjunction is effectively repeated Or, just as Sum is repeated Plus:
Represent Disjunction in terms of Sum:
Text
Wolfram Research (2008), Disjunction, Wolfram Language function, https://reference.wolfram.com/language/ref/Disjunction.html.
CMS
Wolfram Language. 2008. "Disjunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Disjunction.html.
APA
Wolfram Language. (2008). Disjunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Disjunction.html