WOLFRAM SYSTEM MODELER
LinearizedStateSpaceExample for demonstrating the linearized state space modeling environment |
|
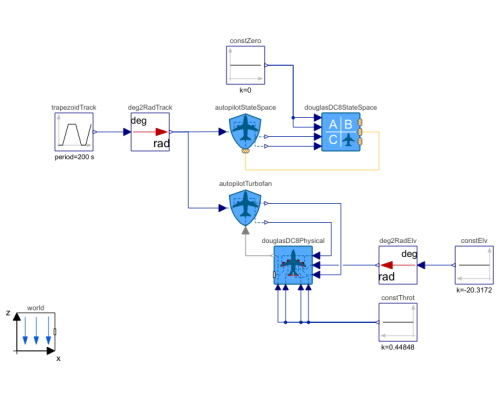
Diagram
Wolfram Language
SystemModel["Aircraft.Examples.LinearizedStateSpace"]
Information
Comparing the State Space and Physical Models for Flying Douglas DC-8
In this example, the Aircraft.StateSpace and Aircraft.Physical aircraft models of the Douglas DC-8 are flown for level flight with moderate turns of 5 degrees first right and then left.
For both aircraft models, only the track angle ais controlled by the autopilot, which consequently control the ailerons and rudders for both aircraft. The state space model of the Douglas DC-8 will calculate at initialization the required throttle position and elevator deflection angle for trimmed conditions for the given altitude and velocity. For the physical model, the constant signals for throttle position and elevator deflection angle also correspond to trimmed conditions for steady level flight in the given flight condition and their values are solved separately.
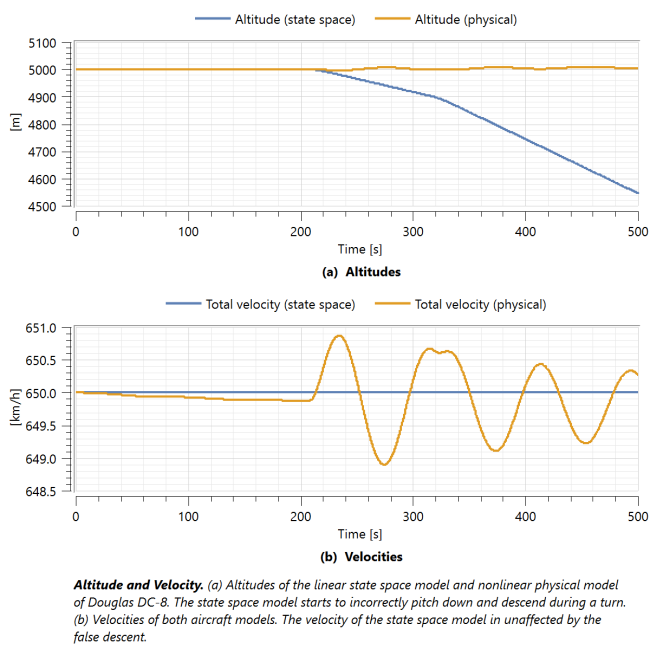
The idea of this example is to show that the linear state space models in this library only work well for studying flight with small deviations from the trimmed reference flight conditions, around which the linearization is defined, whereas the nonlinear physical models will not be distorted when flight conditions change. In this example, the state space model will get considerably distorted as the aircraft turns and there is a yaw rate (r) with a nonzero roll angle (φ). This induces a change in pitch angle (θ), as can be seen in the relation between the Euler rates and body angular velocities [1].
The distortion is due to the assumption in the state space representation for an aircraft (Aircraft.StateSpace.Blocks.longitudinalMotion) on
which creates a disagreement with the pitch angle that is used for solving the longitudinal equations of motion and the pitch angle that is used to solve the position and orientation of the aircraft [2]. Thus, we can see in the default plot how the state space model aircraft seems to pitch down as it turns but continues at the same velocity despite elevator deflection and throttle position remaining the same. The figure also shows that the nonlinear physical model aircraft still accumulates some extremely minor deviations in altitude and velocity even though it was initialized for trimmed conditions as accurately as possible. This is due to the changing dynamics as the mass properties change with the burning of the fuel.
References
[1] Nelson, R. C. (1998). Flight Stability and Automatic Control. 2nd ed. McGraw-Hill. Available at: http://home.eng.iastate.edu/~shermanp/AERE355/lectures/Flight_Stability_and_Automatic_Control_N.pdf.
[2] Cook, M. A. (2012). Flight Dynamics Principles. 2nd ed. Butterworth Heinemann.
Parameters (2)
Components (11)
| deg2RadTrack |
Type: From_deg Description: Convert from degree to radian |
|
|---|---|---|
| autopilotStateSpace |
Type: AutopilotStateSpace Description: Autopilot with default setup for state space models |
|
| douglasDC8StateSpace |
Type: DouglasDC8 Description: Model of Douglas DC-8 using state-space representation |
|
| trapezoidTrack |
Type: Trapezoid Description: Generate trapezoidal signal of type Real |
|
| constZero |
Type: Constant Description: Generate constant signal of type Real |
|
| autopilotTurbofan |
Type: AutopilotTurbofan Description: Autopilot for passenger aircraft with turbofan propulsion |
|
| douglasDC8Physical |
Type: DouglasDC820 Description: Narrow-body turbojet airliner: Douglas DC-8-20 |
|
| constThrot |
Type: Constant Description: Constant throttle position signal (trimmed) |
|
| constElv |
Type: Constant Description: Constant elevator deflection signal (trimmed) |
|
| deg2RadElv |
Type: From_deg Description: Convert from degree to radian |
|
| world |
Type: World Description: World coordinate system used in aircraft libray |