WOLFRAM SYSTEM MODELER
BearingComparisonComparison bearings from a selection list |
 |
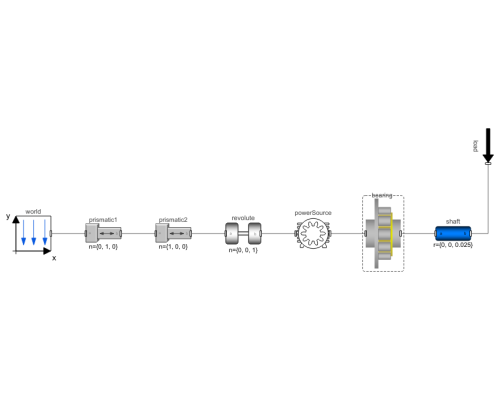
Diagram
Wolfram Language
In[1]:=
SystemModel["RotatingMachinery.Examples.BearingAnalysis.BearingComparison"]
Out[1]:=
Information
Comparing Selected Bearings
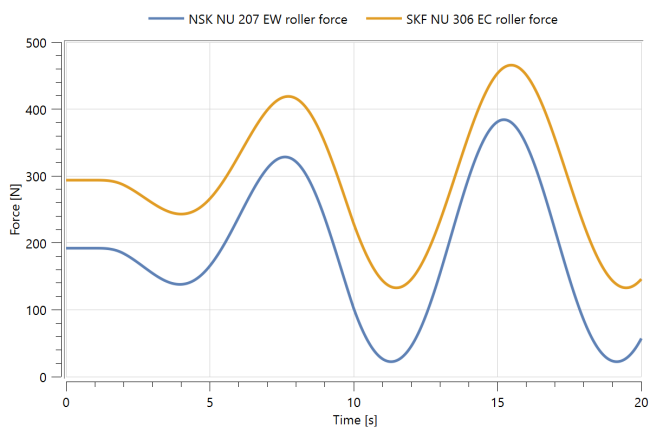
This example compares the performance of two cylindrical bearings.
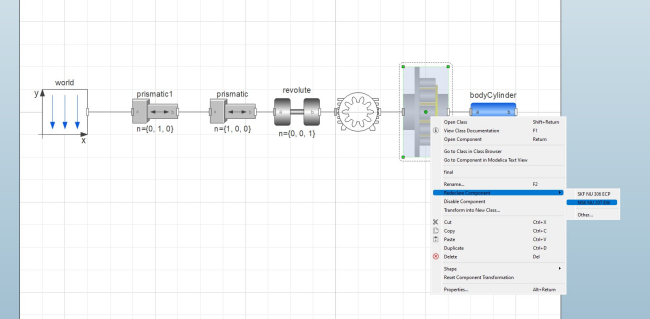
The cylindrical bearings are of the type SKF NU 306 ECP and NSK NU 207 EW. It is possible to switch between these two options by right-clicking the bearing and choosing the desired bearing under Redeclare Component, as shown in Figure 1. Please note that it is necessary to run the simulation for one bearing to store its results, then come back to the Model Center and redeclare it.
Figure 1: Redeclaration of bearing in Model Center.
Now, it is possible to compare any outcome of these two bearings. For instance, the roller forces of the NSK NU 207 EW are smaller, which is an indication of less deflection.
Figure 2: Roller forces comparison.
Parameters (1)
| appliedLoad |
Value: -1000 Type: Force (N) Description: The load applied to the shaft |
|---|
Components (8)
 |
world |
Type: World Description: World coordinate system + gravity field + default animation definition |
|---|---|---|
 |
bearing |
Type: NSK_NU_207_EW Description: Roller bearing parameterized with values corresponding to NSK NU 207 EW |
 |
shaft |
Type: BodyCylinder Description: Rigid body with cylinder shape. Mass and animation properties are computed from cylinder data and density (12 potential states) |
 |
powerSource |
Type: Motor Description: Class for applying a torque to generate a desired angular velocity |
 |
revolute |
Type: Revolute Description: Revolute joint (1 rotational degree-of-freedom, 2 potential states, optional axis flange) |
 |
prismatic2 |
Type: Prismatic Description: Prismatic joint (1 translational degree-of-freedom, 2 potential states, optional axis flange) |
|
prismatic1 |
Type: Prismatic Description: Prismatic joint (1 translational degree-of-freedom, 2 potential states, optional axis flange) |
 |
load |
Type: Force Description: Class that can apply forces along x, y and z axes with a defined interval and amplitude |