BeniniDistribution[α,β,σ]
represents a Benini distribution with shape parameters α and β and scale parameter σ.


BeniniDistribution
BeniniDistribution[α,β,σ]
represents a Benini distribution with shape parameters α and β and scale parameter σ.
Details
- BeniniDistribution is also known as log-Rayleigh distribution.
- The probability density for value
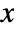 in a Benini distribution is proportional to
in a Benini distribution is proportional to 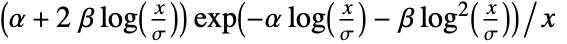 for
for 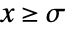 .
. - BeniniDistribution allows α, β, and σ to be any positive real numbers.
- BeniniDistribution allows σ to be a quantity of any unit dimension, and α and β to be dimensionless units. »
- BeniniDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- BeniniDistribution[α,β,σ] represents a continuous statistical distribution defined over the interval
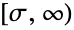 and parametrized by two positive values α, β known as "shape parameters" that determine the overall behavior of the probability density function (PDF). σ is a positive value known as a "location parameter" due to its determination of the horizontal location of the Benini distribution's PDF, though σ is also a "scaling parameter" in the sense that high values of σ correspond to PDFs with shorter overall height. Depending on the values of α and β, the PDF of the Benini distribution may be monotonic decreasing or may be unimodal with potential singularities approaching the leftmost boundary of its domain. The tails of the PDF may be "fat" (in the sense that the PDF decreases algebraically rather than decreasing exponentially for large values
and parametrized by two positive values α, β known as "shape parameters" that determine the overall behavior of the probability density function (PDF). σ is a positive value known as a "location parameter" due to its determination of the horizontal location of the Benini distribution's PDF, though σ is also a "scaling parameter" in the sense that high values of σ correspond to PDFs with shorter overall height. Depending on the values of α and β, the PDF of the Benini distribution may be monotonic decreasing or may be unimodal with potential singularities approaching the leftmost boundary of its domain. The tails of the PDF may be "fat" (in the sense that the PDF decreases algebraically rather than decreasing exponentially for large values 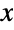 ) or "thin" (the PDF decreases exponentially for large
) or "thin" (the PDF decreases exponentially for large 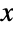 ), depending on the parameters α and β. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.)
), depending on the parameters α and β. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) - Benini distributions were formulated by Italian statistician Rodolfo Benini, who noticed that a quadratic polynomial in the expression
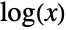 often provided a better fit to models than the degree-one polynomials used by Vilfredo Pareto in the construction of the ParetoDistribution. Since their creation, Benini distributions have become foundational tools in a number of areas due to their potential to measure a vast array of phenomena, including failure rate considerations in actuarial science and income distributions in economics.
often provided a better fit to models than the degree-one polynomials used by Vilfredo Pareto in the construction of the ParetoDistribution. Since their creation, Benini distributions have become foundational tools in a number of areas due to their potential to measure a vast array of phenomena, including failure rate considerations in actuarial science and income distributions in economics. - RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Benini distribution. Distributed[x,BeniniDistribution[α,β,σ]], written more concisely as xBeniniDistribution[α,β,σ], can be used to assert that a random variable x is distributed according to a Benini distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[BeniniDistribution[α,β,σ],x] and CDF[BeniniDistribution[α,β,σ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a Benini distribution, EstimatedDistribution to estimate a Benini parametric distribution from given data, and FindDistributionParameters to fit data to a Benini distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Benini distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Benini distribution.
- TransformedDistribution can be used to represent a transformed Benini distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Benini distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Benini distributions.
- The Benini distribution is related to a number of other distributions. As previously noted, BeniniDistribution is a natural generalization of ParetoDistribution and, indeed, PDF[BeniniDistribution[α,0,σ],x] is precisely the same as PDF[ParetoDistribution[α,σ],x]. BeniniDistribution is also a transformation of RayleighDistribution, in the sense that if a random variate
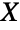 satisfies XRayleighDistribution[σ], then Exp[X]BeniniDistribution[0,1/(2σ2),1]. BeniniDistribution is sometimes referred to as the log-Weibull distribution, in the sense that the CDF of the logarithm of a variate distributed according to WeibullDistribution is the same as the CDF of a Benini-distributed variate, and because of this relationship, BeniniDistribution is also closely related to GammaDistribution, ExponentialDistribution, MaxStableDistribution, MinStableDistribution, GumbelDistribution, FrechetDistribution, and UniformDistribution.
satisfies XRayleighDistribution[σ], then Exp[X]BeniniDistribution[0,1/(2σ2),1]. BeniniDistribution is sometimes referred to as the log-Weibull distribution, in the sense that the CDF of the logarithm of a variate distributed according to WeibullDistribution is the same as the CDF of a Benini-distributed variate, and because of this relationship, BeniniDistribution is also closely related to GammaDistribution, ExponentialDistribution, MaxStableDistribution, MinStableDistribution, GumbelDistribution, FrechetDistribution, and UniformDistribution.
Examples
open all close allBasic Examples (4)
Scope (8)
Generate a sample of pseudorandom numbers from a Benini distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Skewness varies with the shape parameters:
Kurtosis varies with the shape parameters:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (3)
BeniniDistribution can be used to model the weight of cats:
Fit Benini distribution to the data:
Compare the histogram of the data to the PDF of the estimated distribution:
Find the average weight of a cat:
Find the median weight of a cat:
Show that the estimated distribution has a heavy right tail:
Find the probability that a cat weighs at least 3 kg:
Simulated weights for a group of 30 cats:
BeniniDistribution can be used to model losses:
Remove the clear outlier, Andrew, the most destructive hurricane, and add currency units:
Fit generalized beta distribution to the data:
Compare the histogram of the data with the PDF of the estimated distribution:
Find the probability that a loss caused by a hurricane is over 3 billion dollars:
Find the mean hurricane loss in US dollars:
Simulate possible losses for the next 30 strong hurricanes in millions of US dollars:
Find stationary renewal distribution associated with a BenktanderGibratDistribution:
Compare it with BeniniDistribution:
Properties & Relations (5)
Benini distribution is closed under scaling by a positive factor:
The σ parameter behaves as both scale and location parameter:
Relationships to other distributions:
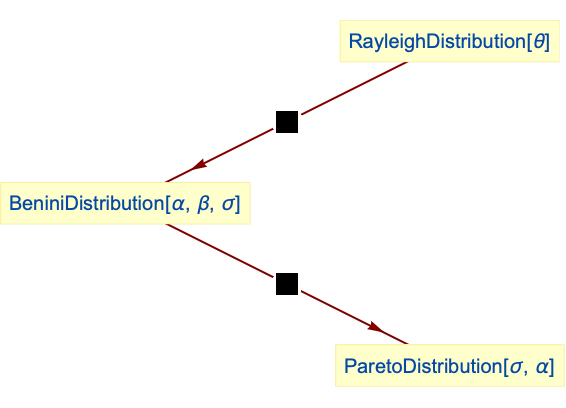
ParetoDistribution is a special case of BeniniDistribution:
Benini distribution is a transformation of RayleighDistribution:
See Also
Related Guides
Text
Wolfram Research (2010), BeniniDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/BeniniDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "BeniniDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/BeniniDistribution.html.
APA
Wolfram Language. (2010). BeniniDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BeniniDistribution.html
BibTeX
@misc{reference.wolfram_2025_beninidistribution, author="Wolfram Research", title="{BeniniDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/BeniniDistribution.html}", note=[Accessed: 05-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_beninidistribution, organization={Wolfram Research}, title={BeniniDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/BeniniDistribution.html}, note=[Accessed: 05-February-2026]}