Global Aspects of Wolfram System Sessions
Global Aspects of Wolfram System Sessions
| The Main Loop | Memory Management |
| Dialogs | Global System Information |
| Date and Time Functions | Wolfram System Sessions |
In any interactive session, the Wolfram System effectively operates in a loop. It waits for your input, processes the input, prints the result, then goes back to waiting for input again. As part of this "main loop", the Wolfram System maintains and uses various global objects. You will often find it useful to work with these objects.
You should realize, however, that if you use the Wolfram System through a special front end, your front end may set up its own main loop, and what is said here may not apply.
| In[n] | the expression on the n th input line |
| InString[n] | the textual form of the n th input line |
| %n or Out[n] | the expression on the n th output line |
| Out[{n1,n2,…}] | a list of output expressions |
| %%…%
(
n
times) or
Out[-n] | the expression on the n th previous output line |
| MessageList[n] | a list of messages produced while processing the n th line |
| $Line |
the current line number (resettable)
|
In a standard interactive session, there is a sequence of input and output lines. The Wolfram System stores the values of the expressions on these lines in In[n] and Out[n].
As indicated by the usual In[n]:= prompt, the input expressions are stored with delayed assignments. This means that whenever you ask for In[n], the input expression will always be reevaluated in your current environment.
This gives the textual form of the second input line, appropriate for editing or other textual manipulation:
| $HistoryLength | the number of previous lines of input and output to keep |
The Wolfram System by default stores all your input and output lines for the duration of the session. In a very long session, this may take up a large amount of computer memory. You can nevertheless get rid of the input and output lines by explicitly clearing the values of In and Out, using Unprotect[In,Out], followed by Clear[In,Out]. You can also tell the Wolfram System to keep only a limited number of lines of history by setting the global variable $HistoryLength.
Note that at any point in a session, you can reset the line number counter $Line, so that, for example, new lines are numbered so as to overwrite previous ones.
| $PreRead | a function applied to each input string before being fed to the Wolfram System |
| $Pre | a function applied to each input expression before evaluation |
| $Post | a function applied to each expression after evaluation |
| $PrePrint | a function applied after Out[n] is assigned, but before the result is printed |
| $SyntaxHandler | a function applied to any input line that yields a syntax error |
The Wolfram System provides a variety of "hooks" that allow you to insert functions to be applied to expressions at various stages in the main loop. Thus, for example, any function you assign as the value of the global variable $Pre will automatically be applied before evaluation to any expression you give as input.
For a particular input line, the standard main loop begins by getting a text string of input. Particularly if you need to deal with special characters, you may want to modify this text string before it is further processed by the Wolfram System. You can do this by assigning a function as the value of the global variable $PreRead. This function will be applied to the text string, and the result will be used as the actual input string for the particular input line.
You can remove the value for $PreRead like this, at least so long as your definition for $PreRead does not modify this very input string:
Once the Wolfram System has successfully read an input expression, it then evaluates this expression. Before doing the evaluation, the Wolfram System applies any function you have specified as the value of $Pre, and after the evaluation, it applies any function specified as the value of $Post. Note that unless the $Pre function holds its arguments unevaluated, the function will have exactly the same effect as $Post.
$Post allows you to specify arbitrary "postprocessing" to be done on results obtained from the Wolfram System. Thus, for example, to make the Wolfram System get a numerical approximation to every result it generates, all you need do is to set $Post=N.
This tells the Wolfram System to apply N to every result it generates:
As soon as the Wolfram System has generated a result, and applied any $Post function you have specified, it takes the result and assigns it as the value of Out[$Line]. The next step is for the Wolfram System to print the result. However, before doing this, it applies any function you have specified as the value of $PrePrint.
This removes the value you assigned to $PrePrint:
There are various kinds of output generated in a typical Wolfram System session. In general, each kind of output is sent to a definite output channel, as discussed in "Streams and Low-Level Input and Output". Associated with each output channel there is a global variable that gives a list of the output streams to be included in that output channel.
| $Output | standard output and text generated by Print |
| $Echo | |
| $Urgent | input prompts and other urgent output |
| $Messages | standard messages and output generated by Message |
By modifying the list of streams in a given output channel, you can redirect or copy particular kinds of Wolfram System output. Thus, for example, by opening an output stream to a file, and including that stream in the $Echo list, you can get each piece of input you give to the Wolfram System saved in a file.
| Streams[] | list of all open streams |
| Streams["name"] | list of all open streams with the specified name |
| $Input | the name of the current input stream |
| $InputFileName | the full absolute path to the file from which input is currently being sought |
The function Streams shows you all the input, output, and other streams that are open at a particular point in a Wolfram System session. The variable $Input gives the name of the current stream from which the Wolfram System input is being taken at a particular point. $Input is reset, for example, during the execution of a Get command. Get also sets $InputFileName to the full absolute path of the file from which input is read.
| $MessagePrePrint | a function to be applied to expressions that are given in messages |
| $Language | list of default languages to use for messages |
There are various global parameters that determine the form of messages generated by the Wolfram System.
As discussed in "Messages", typical messages include a sequence of expressions that are combined with the text of the message through StringForm. $MessagePrePrint gives a function to be applied to the expressions before they are printed. The default for $MessagePrePrint uses Short for text formatting and a combination of Short and Shallow for typesetting.
As discussed in "International Messages", the Wolfram System allows you to specify the language in which you want messages to be produced. In a particular Wolfram System session, you can assign a list of language names as the value of $Language.
| Exit[] or Quit[] | terminate your Wolfram System session |
| $Epilog | a global variable to be evaluated before termination |
The Wolfram System will continue in its main loop until you explicitly tell it to exit. Most Wolfram System interfaces provide special ways to do this. Nevertheless, you can always do it by explicitly calling Exit or Quit.
The Wolfram System allows you to give a value to the global variable $Epilog to specify operations to perform just before the Wolfram System actually exits. In this way, you can, for example, make the Wolfram System always save certain objects before exiting.
| $IgnoreEOF | whether to ignore the end‐of‐file character |
As discussed in "Special Characters: Strings and Characters", the Wolfram System usually does not treat special characters in a special way. There is one potential exception, however. With the default setting $IgnoreEOF=False, the Wolfram System recognizes end‐of‐file characters. If the Wolfram System receives an end‐of‐file character as the only thing on a particular input line in a standard interactive Wolfram System session, then it will exit the session.
Exactly how you enter an end‐of‐file character depends on the computer system you are using. Under Unix, for example, you typically press Ctrl+D.
Note that if you use the Wolfram System in a "batch mode", with all its input coming from a file, then it will automatically exit when it reaches the end of the file, regardless of the value of $IgnoreEOF.
Within a standard interactive session, you can create "subsessions" or dialogs using the Wolfram Language command Dialog. Dialogs are often useful if you want to interact with the Wolfram Language while it is in the middle of doing a calculation. As mentioned in "Tracing Evaluation", TraceDialog for example automatically calls Dialog at specified points in the evaluation of a particular expression. In addition, if you interrupt the Wolfram Language during a computation, you can typically "inspect" its state using a dialog.
| Dialog[] | initiate a Wolfram Language dialog |
| Dialog[expr] | initiate a dialog with expr as the current value of % |
| Return[] | return from a dialog, taking the current value of % as the return value |
| Return[expr] | return from a dialog, taking expr as the return value |
You can use Return to exit from a dialog:
When you exit a dialog, you can return a value for the dialog using Return[expr]. If you do not want to return a value, and you have set $IgnoreEOF=False, then you can also exit a dialog simply by giving an end‐of‐file character, at least on systems with text‐based interfaces.
In starting a dialog, you will often find it useful to have some "initial expression". If you use Dialog[expr], then the Wolfram Language will start a dialog, using expr as the initial expression, accessible for example as the value of %.
This returns a value from the first dialog, and starts the second dialog, with initial expression b+c:
This returns a value from the second dialog. The final result is the original expression, with values from the two dialogs inserted:
Dialog effectively works by running a subsidiary version of the standard Wolfram Language main loop. Each dialog you start effectively "inherits" various values from the overall main loop. Some of the values are, however, local to the dialog, so their original values are restored when you exit the dialog.
Thus, for example, dialogs inherit the current line number $Line when they start. This means that the lines in a dialog have numbers that follow the sequence used in the main loop. Nevertheless, the value of $Line is local to the dialog. As a result, when you exit the dialog, the value of $Line reverts to what it was in the main loop.
If you start a dialog on line 10 of your Wolfram Language session, then the first line of the dialog will be labeled In[11]. Successive lines of the dialog will be labeled In[12], In[13], and so on. Then, when you exit the dialog, the next line in your main loop will be labeled In[11]. At this point, you can still refer to results generated within the dialog as Out[11], Out[12], and so on. These results will be overwritten, however, when you reach lines In[12], In[13], and so on in the main loop.
In a standard Wolfram Language session, you can tell whether you are in a dialog by seeing whether your input and output lines are indented. If you call a dialog from within a dialog, you will get two levels of indentation. In general, the indentation you get inside d nested dialogs is determined by the output form of the object DialogIndent[d]. By defining the format for this object, you can specify how dialogs should be indicated in your Wolfram Language session.
| DialogSymbols:>{x,y,…} | symbols whose values should be treated as local to the dialog |
| DialogSymbols:>{x=x0,y=y0,…} | symbols with initial values |
| DialogProlog:>expr | an expression to evaluate before starting the dialog |
Options for Dialog.
Whatever setting you give for DialogSymbols, Dialog will always treat the values of $Line, $Epilog, and $MessageList as local. Note that if you give a value for $Epilog, it will automatically be evaluated when you exit the dialog.
When you call Dialog, its first step is to localize the values of variables. Then it evaluates any expression you have set for the option DialogProlog. If you have given an explicit argument to the Dialog function, this is then evaluated next. Finally, the actual dialog is started.
When you exit the dialog, you can explicitly specify the return value using Return[expr]. If you do not do this, the return value will be taken to be the last value generated in the dialog.
| DateList[] | give the current local date and time in the form {year,month,day,hour,minute,second} |
| DateList[TimeZone->z] | give the current date and time in time zone z |
| $TimeZone | give the time zone assumed by your computer system |
The Wolfram Language DateList function returns whatever your computer system gives as the current date and time. It assumes that any corrections for daylight saving time and so on have already been done by your computer system. In addition, it assumes that your computer system has been set for the appropriate time zone.
The variable $TimeZone returns the current time zone assumed by your computer system. The time zone is given as the number of hours which must be added to Greenwich Mean Time (GMT) to obtain the correct local time. Thus, for example, U.S. Eastern Standard Time (EST) corresponds to time zone 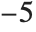 . Note that daylight saving time corrections must be included in the time zone, so U.S. Eastern Daylight Time (EDT) corresponds to time zone
. Note that daylight saving time corrections must be included in the time zone, so U.S. Eastern Daylight Time (EDT) corresponds to time zone 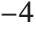 .
.
| AbsoluteTime[] |
total number of seconds since the beginning of January 1, 1900
|
| SessionTime[] | total number of seconds elapsed since the beginning of your current Wolfram System session |
| TimeUsed[] | total number of seconds of CPU time used in your current Wolfram System session |
| $TimeUnit | the minimum time interval recorded on your computer system |
You should realize that on any computer system, there is a certain "granularity" in the times that can be measured. This granularity is given as the value of the global variable $TimeUnit. Typically it is either about 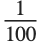 or
or 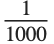 of a second.
of a second.
| Pause[n] | pause for at least n seconds |
This pauses for 10 seconds, then reevaluates the time functions. Note that TimeUsed[] is not affected by the pause:
| AbsoluteTime[date] | convert from date to absolute time |
| DateList[time] | convert from absolute time to date |
| DateList["string"] | convert a date string to a date list |
| DateList[{"string",{"e1","e2",…}}] | give the date list obtained by extracting elements "ei" from "string" |
You can use DateList["string"] to convert a date string into a date list, as long as the date format is sufficiently unambiguous.
For more control of the conversion, you can specify the order and type of date elements appearing in the string. The elements can be strings like "Year", "Quarter", "Month", "MonthName", "Day", "DayName", "Hour", "AMPM", "Minute", or "Second".
If the date element delimiters contain letters or digits, these must also be specified as part of the date elements.
| DateString[] | give a string representing current local date and time |
| DateString[datespec,elems] | give elements elems of date and time given by datespec |
DateString is used to give a nice string representation of a date and time. The exact output format can be specified from a long list of date elements, such as "DateTime", "DayName", "HourShort", etc.
| DatePattern[elems] | string pattern matching a date with the given elements |
You can use DatePattern[elems] as a string pattern in string matching functions. The date elements are the same as used in DateList, although the default date element delimiters are restricted to the /, -, :, or . characters. Other delimiters can be given explicitly in the list of date elements.
| DateListPlot[list] | generate a plot from a list of data with date coordinates |
| DateListPlot[list,datespec] | generate a plot from a list of data with dates specified by datespec |
| DateListLogPlot[list] | generate a linear-log plot from a list of data with date coordinates |
| DateListLogPlot[list,datespec] | generate a linear-log plot from a list of data with dates specified by datespec |
DateListPlot can be used to plot data with date or time horizontal coordinates. Dates can be lists, strings, or absolute times as with DateList, DateString, and AbsoluteTime. A date specification datespec can be given to associate dates with data given as {y1,y2,…}. DateListLogPlot allows you to plot the data with a logarithmic vertical scale.
| Timing[expr] | evaluate expr, and return a list of the CPU time needed, together with the result obtained |
| AbsoluteTiming[expr] | evaluate expr, giving the absolute time taken |
Timing allows you to measure the CPU time associated with the evaluation of a single Wolfram Language expression. Timing corresponds to the increase in TimeUsed. Note that only CPU time associated with the actual evaluation of the expression within the Wolfram Language kernel is included. The time needed to format the expression for output, and any time associated with external programs, is not included.
AbsoluteTiming allows you to measure absolute total elapsed time. You should realize, however, that the time reported for a particular calculation by both AbsoluteTiming and Timing depends on many factors.
First, the time depends in detail on the computer system you are using. It depends not only on instruction times, but also on memory caching, as well as on the details of the optimization done in compiling the parts of the internal code of the Wolfram Language used in the calculation.
The time also depends on the precise state of your Wolfram Language session when the calculation was done. Many of the internal optimizations used by the Wolfram Language depend on details of preceding calculations. For example, the Wolfram Language often uses previous results it has obtained, and avoids unnecessarily reevaluating expressions. In addition, some Wolfram Language functions build internal tables when they are first called in a particular way, so that if they are called in that way again, they run much faster. For all of these kinds of reasons, it is often the case that a particular calculation may not take the same amount of time if you run it at different points in the same Wolfram Language session.
This gives the CPU time needed for the calculation. The semicolon causes the result of the calculation to be given as Null:
Now the Wolfram Language has built internal tables for factorial functions, and the calculation takes no measurable CPU time:
Note that the results you get from Timing are only accurate to the timing granularity $TimeUnit of your computer system. Thus, for example, a timing reported as 0 could in fact be as much as $TimeUnit.
| TimeConstrained[expr,t] | try to evaluate expr, aborting the calculation after t seconds |
| TimeConstrained[expr,t,failexpr] | return failexpr if the time constraint is not met |
When you use the Wolfram Language interactively, it is quite common to try doing a calculation, but to abort the calculation if it seems to be taking too long. You can emulate this behavior inside a program by using TimeConstrained. TimeConstrained tries to evaluate a particular expression for a specified amount of time. If it does not succeed, then it aborts the evaluation, and returns either $Aborted, or an expression you specify.
You can use TimeConstrained, for example, to have the Wolfram Language try a particular approach to a problem for a certain amount of time, and then to switch to another approach if the first one has not yet succeeded. You should realize however that TimeConstrained may overrun the time you specify if the Wolfram Language cannot be interrupted during a particular part of a calculation. In addition, you should realize that because different computer systems run at different speeds, programs that use TimeConstrained will often give different results on different systems.
| MemoryInUse[] | number of bytes of memory currently being used by the Wolfram System |
| MaxMemoryUsed[] | maximum number of bytes of memory used by the Wolfram System in this session |
Particularly for symbolic computations, memory is usually the primary resource which limits the size of computations you can do. If a computation runs slowly, you can always potentially let it run longer. But if the computation generates intermediate expressions which simply cannot fit in the memory of your computer system, then you cannot proceed with the computation.
The Wolfram System is careful about the way it uses memory. Every time an intermediate expression you have generated is no longer needed, the Wolfram System immediately reclaims the memory allocated to it. This means that at any point in a session, the Wolfram System stores only those expressions that are actually needed; it does not keep unnecessary objects which have to be "garbage collected" later.
This list is kept because it is the value of Out[41]. If you clear Out[41], the list is no longer needed:
One issue that often comes up is exactly how much memory the Wolfram System can actually use on a particular computer system. Usually there is a certain amount of memory available for all processes running on the computer at a particular time. Sometimes this amount of memory is equal to the physical number of bytes of RAM in the computer. Often, it includes a certain amount of "virtual memory", obtained by swapping data on and off a mass storage device.
When the Wolfram System runs, it needs space both for data and for code. The complete code of the Wolfram System is typically several megabytes in size. For any particular calculation, only a small fraction of this code is usually used. However, in trying to work out the total amount of space available for Wolfram System data, you should not forget what is needed for Wolfram Language code. In addition, you must include the space that is taken up by other processes running in the computer. If there are fewer jobs running, you will usually find that your job can use more memory.
It is also worth realizing that the time needed to do a calculation can depend very greatly on how much physical memory you have. Although virtual memory allows you in principle to use large amounts of memory space, it is usually hundreds or even thousands of times slower to access than physical memory. As a result, if your calculation becomes so large that it needs to make use of virtual memory, it may run much more slowly.
| MemoryConstrained[expr,b] | try to evaluate expr, aborting if more than b additional bytes of memory are requested |
| MemoryConstrained[expr,b,failexpr] | return failexpr if the memory constraint is not met |
MemoryConstrained works much like TimeConstrained. If more than the specified amount of memory is requested, MemoryConstrained attempts to abort your computation. As with TimeConstrained, there may be some overshoot in the actual amount of memory used before the computation is aborted.
| ByteCount[expr] | the maximum number of bytes of memory needed to store expr |
| LeafCount[expr] | the number of terminal nodes in the expression tree for expr |
Although you may find ByteCount useful in estimating how large an expression of a particular kind you can handle, you should realize that the specific results given by ByteCount can differ substantially from one version of the Wolfram System to another.
Another important point is that ByteCount always gives you the maximum amount of memory needed to store a particular expression. Often the Wolfram System will actually use a much smaller amount of memory to store the expression. The main issue is how many of the subexpressions in the expression can be shared.
In an expression like f[1+x,1+x], the two subexpressions 1+x are identical, but they may or may not actually be stored in the same piece of computer memory. ByteCount gives you the number of bytes needed to store expressions with the assumption that no subexpressions are shared. You should realize that the sharing of subexpressions is often destroyed as soon as you use an operation like the /. operator.
Nevertheless, you can explicitly tell the Wolfram Language to share subexpressions using the function Share. In this way, you can significantly reduce the actual amount of memory needed to store a particular expression.
| Share[expr] | share common subexpressions in the storage of expr |
| Share[] | share common subexpressions throughout memory |
On most computer systems, the memory used by a running program is divided into two parts: memory explicitly allocated by the program, and "stack space". Every time an internal routine is called in the program, a certain amount of stack space is used to store parameters associated with the call. On many computer systems, the maximum amount of stack space that can be used by a program must be specified in advance. If the specified stack space limit is exceeded, the program usually just exits.
In the Wolfram System, one of the primary uses of stack space is in handling the calling of one Wolfram Language function by another. All such calls are explicitly recorded in the Wolfram System Stack discussed in "The Evaluation Stack". You can control the size of this stack by setting the global parameter $RecursionLimit. You should be sure that this parameter is set small enough that you do not run out of stack space on your particular computer system.
In order to write the most general Wolfram Language programs you will sometimes need to find out global information about the setup under which your program is being run.
Thus, for example, to tell whether your program should be calling functions like NotebookWrite, you need to find out whether the program is being run in a Wolfram Language session that is using the notebook front end. You can do this by testing the global variable $Notebooks.
| $Notebooks | whether a notebook front end is being used |
The Wolfram System is usually used interactively, but it can also operate in a batch mode—say taking input from a file and writing output to a file. In such a case, a program cannot for example expect to get interactive input from the user.
| $BatchInput | whether input is being given in batch mode |
| $BatchOutput |
whether output should be given in batch mode, without labeling, etc.
|
The Wolfram Language kernel is a process that runs under the operating system on your computer. Within the Wolfram Language there are several global variables that allow you to find the characteristics of this process and its environment.
| $CommandLine | the original command line used to invoke the Wolfram Language kernel |
| $ParentLink | the WSTP LinkObject specifying the program that invoked the kernel (or Null if the kernel was invoked directly) |
| $ProcessID | the ID assigned to the Wolfram Language kernel process by the operating system |
| $ParentProcessID | the ID of the process that invoked the Wolfram Language kernel |
| $Username | the login name of the user running the Wolfram Language kernel |
| Environment["var"] | the value of a variable defined by the operating system |
If you have a variable such as x in a particular Wolfram Language session, you may or may not want that variable to be the same as an x in another Wolfram Language session. In order to make it possible to maintain distinct objects in different sessions, the Wolfram Language supports the variable $SessionID, which uses information such as starting time, process ID and machine ID to try to give a different value for every single Wolfram Language session, whether it is run on the same computer or a different one.
| $SessionID | a number set up to be different for every Wolfram Language session |
The Wolfram Language provides various global variables that allow you to tell which version of the kernel you are running. This is important if you write programs that make use of features that are, say, new in Version 6. You can then check $VersionNumber to find out if these features will be available.
| $Version | a string giving the complete version of the Wolfram System in use |
| $VersionNumber | the Wolfram Language kernel version number (e.g. 11.2) |
| $ReleaseNumber | the release number for your version of the Wolfram Language kernel on your particular computer system |
| $CreationDate |
The Wolfram System itself is set up to be as independent of the details of the particular computer system on which it is run as possible. However, if you want to access external aspects of your computer system, then you will often need to find out its characteristics.
| $System | a full string describing the computer system in use |
| $SystemID | a short string specifying the computer system in use |
| $ProcessorType | the architecture of the processor in your computer system |
| $MachineType | the general type of your computer system |
| $ByteOrdering | the native byte ordering convention on your computer system |
| $OperatingSystem | the basic operating system in use |
| $SystemCharacterEncoding | the default raw character encoding used by your operating system |
The Wolfram System uses the values of $SystemID to label directories that contain versions of files for different computer systems, as discussed in "Reading and Writing Wolfram Language Files: Files and Streams" and "Portability of WSTP Programs". Computer systems for which $SystemID is the same will normally be binary compatible.
$OperatingSystem has values such as "Windows" or "Unix". By testing $OperatingSystem you can determine whether a particular external program is likely to be available on your computer system.
| $MachineAddresses | the list of current IP addresses |
| $MachineName | the name of the computer on which the Wolfram System is running |
| $MachineDomains | the current network domains for the computer |
| $MachineID | the unique ID assigned by the Wolfram System to the computer |
| $ActivationKey | the activation key under which the Wolfram System is running |
| $LicenseExpirationDate | the date on which the license expires |
| $NetworkLicense | whether this is a network license |
| $LicenseServer | the full name of the machine serving the license |
| $LicenseProcesses | the number of Wolfram System processes currently being run under the license |
| $MaxLicenseProcesses | the maximum number of processes provided by the license |
| $PasswordFile | password file used when the kernel was started |
Command‐Line Options and Environment Variables
| -pwfile | Wolfram System password file |
| -run |
Wolfram Language input to run (kernel only)
|
| -initfile |
Wolfram System initialization file (kernel only)
|
| -noinit |
do not run initialization files (kernel only)
|
| -wstp | communicate only via WSTP |
If the Wolfram System front end is called with a notebook file as a command‐line argument, then this notebook will be made the initial selected notebook. Otherwise, a new notebook will be created for this purpose.
Wolfram Language kernels and front ends can also take additional command‐line options specific to particular window environments.
command‐line environment for the Wolfram System front end | |
command‐line environment for the Wolfram Language kernel | |
setting for $BaseDirectory | |
setting for $UserBaseDirectory |
The Wolfram System will read the values of operating system environment variables, and will use these values in addition to any command-line options explicitly given.
Initialization
- Performs license management operations.
- Runs Wolfram Language commands specified in any -run options passed to the kernel executable.
- Runs the Wolfram Language commands in the systemwide initialization file $BaseDirectory/Kernel/init.m.
- Runs the Wolfram Language commands in the user‐specific initialization file $UserBaseDirectory/Kernel/init.m.
- Loads init.m and Kernel/init.m files in Autoload directories.
- Begins running the main loop.
The Main Loop
- Read in input.
- Apply $PreRead function, if defined, to the input string.
- Print syntax warnings if necessary.
- Apply $SyntaxHandler function if there is a syntax error.
- Assign InString[n].
- Apply $Pre function, if defined, to the input expression.
- Assign In[n].
- Evaluate expression.
- Apply $Post function, if defined.
- Assign Out[n], stripping off any formatting wrappers.
- Apply $PrePrint function, if defined.
- Assign MessageList[n] and clear $MessageList.
- Print expression, if it is not Null.
- Increment $Line.
- Clear any pending aborts.
Note that if you call the Wolfram Language via the Wolfram Symbolic Transfer Protocol (WSTP) from within an external program, then you must effectively create your own main loop, which will usually differ from the one described above.
Messages
During a Wolfram System session messages can be generated either by explicit calls to Message, or in the course of executing other built‐in functions.
| f::name::lang | a message in a specific language |
| f::name | a message in a default language |
| General::name | a general message with a given name |
If no language is specified for a particular message, text for the message is sought in each of the languages specified by $Language. If f::name is not defined, a definition for General::name is sought. If still no message is found, any value defined for $NewMessage is applied to f and "name".
Quiet[expr] evaluates expr while preventing messages from being printed during the evaluation. Off[message] prevents a specified message from ever being printed. Check allows you to determine whether particular messages were generated during the evaluation of an expression. $MessageList and MessageList[n] record all the messages that were generated during the evaluation of a particular line in a Wolfram System session.
Messages are specified as strings to be used as the first argument of StringForm. $MessagePrePrint is applied to each expression to be spliced into the string.
Termination
| Exit[] or Quit[] | terminate the Wolfram System |
| $Epilog | symbol to evaluate before the Wolfram System exits |
| $IgnoreEOF | whether to exit an interactive Wolfram System session when an end‐of‐file character is received |
| end.m | file to read when the Wolfram System terminates |
There are several ways to end a Wolfram System session. If you are using the Wolfram System interactively, typing Exit[] or Quit[] on an input line will always terminate the Wolfram System.
If you are taking input for the Wolfram Language from a file, the Wolfram System will exit when it reaches the end of the file. If you are using the Wolfram System interactively, it will still exit if it receives an end‐of‐file character (typically Ctrl+d). You can stop the Wolfram System from doing this by setting $IgnoreEOF=True.
Network License Management
single-machine license | a process must always run on a specific machine |
network license | a process can run on any machine on a network |
Copies of the Wolfram System can be set up with either single‐machine or network licenses. A network license is indicated by a line in the mathpass file starting with !name, where name is the name of the server machine for the network license.
Network licenses are controlled by the Wolfram System license management program mathlm, which is run on the server machine. This program must be running whenever a Wolfram System with a network license is being used. Typically you will want to set up your system so that mathlm is started whenever the system boots.
■ Type ./mathlm directly on the Unix command line |
■ Add a line to start mathlm in your central system startup script |
When mathlm is not started directly from a command line, it normally sets itself up as a background process, and continues running until it is explicitly terminated. Note that if one mathlm process is running, any other mathlm processes you try to start will automatically exit immediately.
| -logfile file | write a log of license server actions to file |
| -loglevel n |
how verbose to make log entries (1 to 4)
|
| -logformat string | use a log format specified by string |
| -language name |
language to use for messages (default
English
)
|
| -pwfile file | use the specified mathpass file (default ./mathpass) |
| -timeout n | suspend authorization on stopped Wolfram System jobs after n hours |
| -restrict file | use the specified restriction file |
| -mathid |
print the MathID for the license server, then exit
|
| -foreground | run mathlm in the foreground, logging to stdout |
| -install | install mathlm as a Windows service (Microsoft Windows only) |
| -uninstall | uninstall mathlm as a Windows service (Microsoft Windows only) |
| monitorlm | a program to monitor network license activity |
| monitorlm name | monitor activity for license server name |
If monitorlm is run in an environment where a web browser can be started, it will automatically generate HTML output in the browser. Otherwise it will generate plain text.