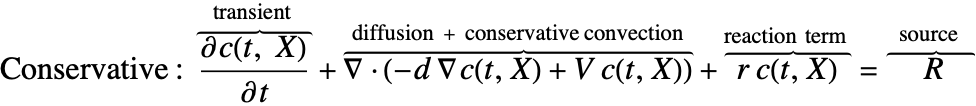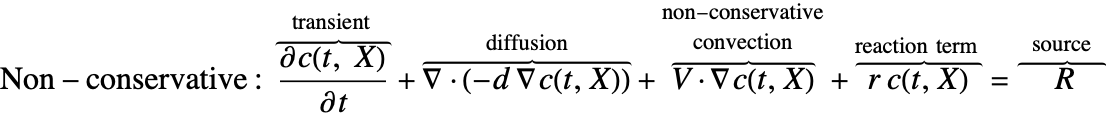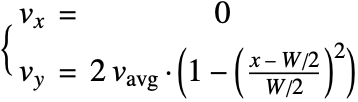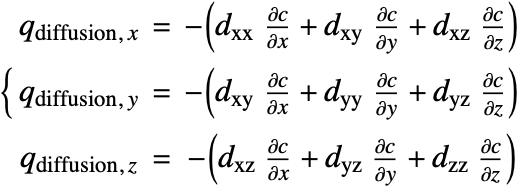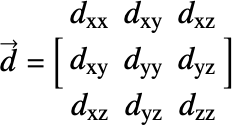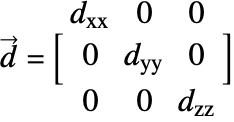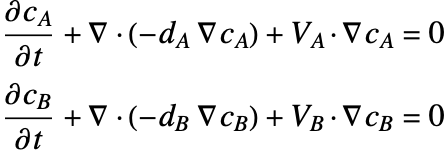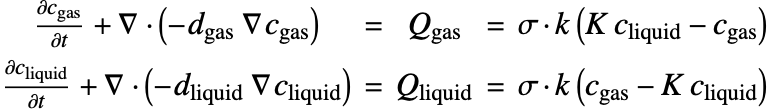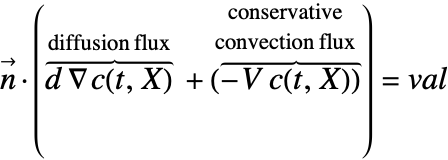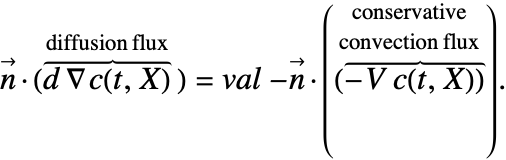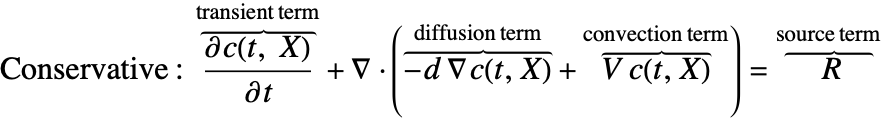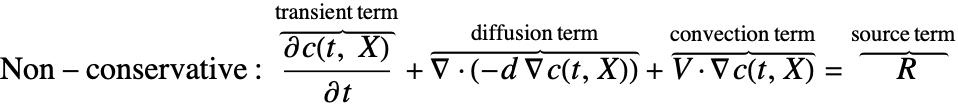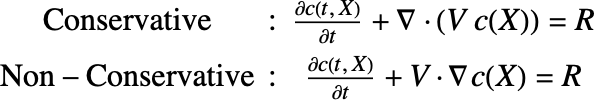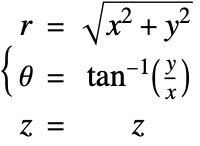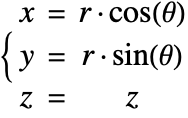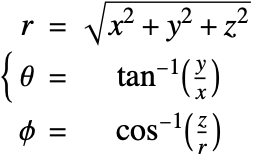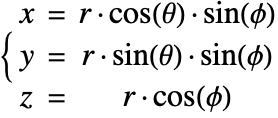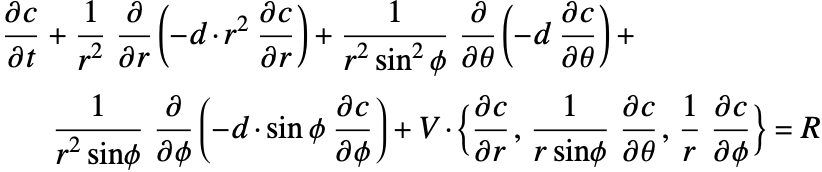物質輸送

はじめに

このチュートリアルでは，希釈種の物質輸送のモデリングの基本を説明する．物質輸送解析を行うのに関連する方程式と境界条件を導出し，解説する．

物質輸送は，化学種の運動に関する化学工学の分野である．物質輸送の2つのメカニズムは物質拡散と物質対流である．物質拡散の動力となるのはさまざまな場所における種濃度の差である．一方，物質対流は種が運動している流体媒体で輸送されるときにのみ発生する．この2つのメカニズムが組み合さると，時間に伴う種濃度場の変化を引き起こし，質量平衡方程式でモデル化される．

このモデリングプロセスは，NDSolveで解くことができる偏微分方程式(PDE)となる．さらにこのチュートリアルでは，いろいろな種類の質量輸送境界条件を紹介する．与えられた境界条件について，さまざまな現実世界の化学種の相互作用をモデル化する方法を示す．

このノートブックは，物質移動をモデル化する方法の基本を提供する．簡単でありながら分かりやすい例を示すことに焦点を置く．物質移動モデリングの産業的な応用例を示す拡張例題は物質移動モデルコレクションで見ることができる．

このノートブックで示されているシミュレーション結果のアニメーションの多くはRasterizeの呼出しで生成されている．これはこのノートブックが必要とするディスク容量を減らすためである．この欠点はアニメーションの視覚的な品質が，呼出しなしの場合ほど鮮明ではないという点である．高品質のグラフィックスが取得したい場合は，Rasterizeの呼び出しを削除するかコメントアウトするとよい．

このチュートリアルで使われているシンボルおよび対応する単位は，用語集セクションに要約されている．

物質平衡方程式

このセクションでは，まず物質平衡方程式を紹介し，その導出方法，Wolfram言語にマップする方法の例を示す．

物質平衡方程式入門

物質拡散および物質対流による化学種の輸送をモデル化するために使うことのできる公式には2種類ある．

物質平衡方程式の従属変数は種濃度 であり，これは時間 と位置 によって変化する．偏微分方程式(PDE)モデルは，化学種が固体媒体あるいは流体媒体中を時間とともにどのように輸送されるかを記述する．

通常，濃度場 が滑らかであると想定される非圧縮性流体には非保存形式が適している．物質平衡方程式の導出セクションの導出方法を見えると，なぜであるかが分かる．

時間微分の部分の他，どちらのPDEもいくつかの成分からできている．まず，種の拡散係数とも言われる拡散係数 を持つ拡散項 がある．場合によっては，拡散係数が温度 や濃度 等の他の特性に依存し，方程式が非線形になることがある．可変拡散係数の詳細は，後のセクション物質の可変拡散係数Coefficientで説明する．

2つ目の成分は対流項である．保存形式では対流項はであり，非保存形式では である．保存形式と非保存形式の違いは物質平衡方程式の導出セクションで説明する．どちらの形式でも，この項は流速 のある流体媒体で物質輸送が起こるときにだけ存在する．シミュレーションの媒体が固体であれば，どちらの形式が使われていようともこの項はゼロとなる．

対流項とは異なり，拡散項は媒体が固体でも流体でも存在する．

項 は，通常化学反応による化学種の物質生成速度あるいは物質消費速度を表す．これについては化学反応のある物質輸送のセクション詳述する．

物質平衡方程式の導出

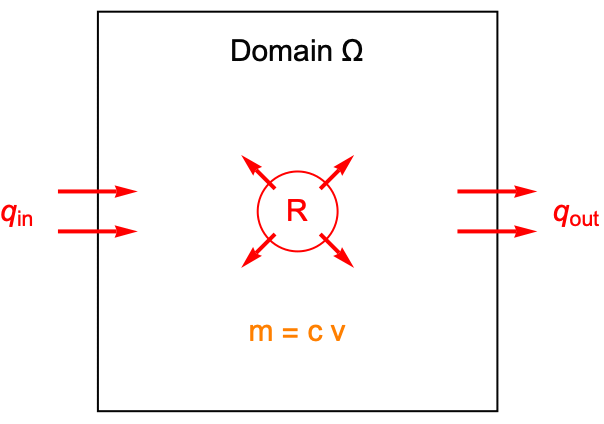
物質平衡方程式を導くために，まず質量保存の法則から始める．システムにおいて，合計の質量変化は質量形成の純量から質量流出の純量を引いたものに等しいはずである．したがって質量平衡は以下のように表すことができる．

物質平衡方程式を定式化するために，化学種の質量が単位体積領域内で平衡となる．質量平衡は種濃度 に基づいており，モルで測定される単位体積当たりの種の量を表している．モル濃度 は以下によって物質濃度 に変換することができる．

ここで はモルでの種の量，は領域の体積，は種の質量，は種の単位モル当たりの質量であるモル質量である．

上のグラフィックスでは が濃度で が領域の面積である．制御面積内の総質量は に等しい．工 は領域内部の化学反応による物質生成の正味速度を表す．正味質量流束 は境界を通して存在する質量流束の正味速度を表す．

上記の2Dにおける考え方はどの次元でも有効である．例えば3D領域では，濃度 はで，体積はで与えられる．

境界を通過する質量流束 の単位は境界の次元に依存する．3D領域では，境界は2D曲面で表現され，質量流束 の単位はである．しかし2D領域では，境界は1Dの直線で構成されるため の単位はになる．1Dでは，境界は無次元の点で表され，熱流束 の単位はである．

領域内の質量保存は以下の方程式で記述することができる．

つまり質量変化速度 は領域内の物質生成正味速度 から領域内に存在する正味質量流束 を引いたものに等しいのである．

ここで質量流束 を，拡散質量流束 と対流質量流束 の2つの部分に分けることができる．拡散流束は質量種濃度の濃度勾配による物質輸送を表し，その拡散率 に比例する：

方程式(1)はフィック(Fick)の法則[2]としても知られている．先頭の負記号は，物質拡散が濃度減少の方向にあることを示している．

対流流束は媒体の流れによって輸送される物質を表し，流速 に比例する：

物質輸送が固体媒体内で起きる場合，固体には定義上内部速度場 がないため，対流項は に設定される．

(3)と(4)を質量保存方程式(5)に代入すると，保存形式の物質輸送モデルになる．

(6)をPDEの係数形式 で表すときは，対流項 の符号に気をつける必要がある．

方程式(7)は，対流物質流束項 および流速 が発散演算子の内部にあるため，保存形式の物質平衡方程式として知られている．

非保存形式を得るためには，連鎖法則を使って方程式(8)を拡張する．

この結果は項 と項 になる．非圧縮性流体の場合，流速の拡散は定義上ゼロ()であるため，項 はゼロに等しく，結果的に非保存形式の物質平衡方程式(9)になる．

物質輸送モデルを解く場合，可能ならば，非圧縮性流体には非保存形式を使うことをお勧めする．以下がその主な理由のうちの2つである．

• 項 を削除することで，非圧縮性流束場 が非物理的な物質生成あるいは消費を生成項 に誘導しないことが確実になる．

• 物質対流項(10)が発散演算子の外側にあることで，解の場[11]のスプリアス振動の成長を阻止し，PDEモデルを解くのにより安定に効率的にする．

しかし，非保存形式は，濃度場 が滑らかであると想定される非圧縮性流体にしか適用できない．圧縮性媒体における物質輸送では，保存形式(12)を使わなければならない．流体流速がゼロの場合，どちらのモデルも同じPDEに簡約される．

このチュートリアルでは非圧縮性流体媒体に焦点を当て，物質輸送モデルのデフォルトPDE設定として非保存形式の物質平衡方程式(13)を使う．しかし，後のセクション物質輸送の境界条件では，保存形式と非保存形式の両方の境界条件の設定を提示する．

物質平衡方程式は円筒座標および球座標で表すこともできる．この詳細は付録セクション物質平衡方程式の特別な場合で述べている．

次のセクションではWolfram言語で物質輸送モデル関数を設定する．

物質輸送モデルの設定

直交座標の物質輸送モデルに必要な入力は次の通りである．

		濃度変数
		空間独立変数
		速度場
		種の拡散率
		反応速度（物質生成速度ともいわれる）

このモデル定義では非アクティブなPDE演算子が使われている．チュートリアル偏微分方程式の数値解法のいくつかのセクションに非アクティブ演算子の使用についての説明がある．

次の数セクションでは，物質輸送モデルについてもっと詳しく説明する．さまざまな種類の物質輸送PDEの使い方を例を使って提示する．

最初の物質輸送の例

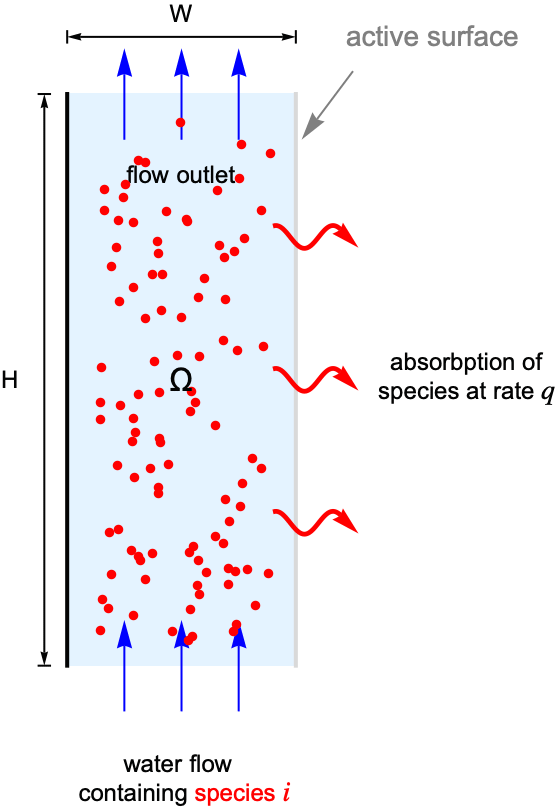
以下に示す2Dの静的な例の目的は，物質輸送モデリングの通常のワークフローを示すことである．

このために，種 が水に溶けた平行板反応器を考える．水流が反応器を通過するとき，種 の一部が右側にある活性表面によって吸収される．ここでの目標は，反応器内の種 の定常状態濃度場を求めることである．

例を具体的にするため，モデル領域に幅 ，高さ を使い，薄い灰色で示された右側の活性表面に吸収速度 を設定する．黒で表示されている左の壁は，種 には不透過であると想定されるため，質量流束は存在しない．

モデル領域を設定する．

この例では，任意の物質拡散係数を使う．

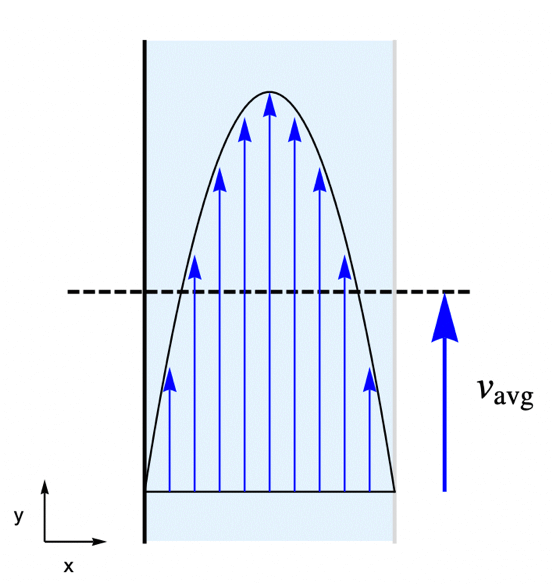
この例では，水は平均速度 で反応器内を通過する．反応器内の流速場 はラミナ断面によって決まる．

次に各境界における境界条件を設定する．物質輸送境界条件の設定の詳細は，セクション物質輸送の境界条件で述べる．

流入口では，その下から種 が無限に供給されるかのように，種濃度は に保たれる．

活性表面では，種 が指定された速度 で継続的に吸収される．これは質量流束境界条件でモデル化される．

活性表面で質量流束境界条件を設定する．

左側の壁は種 が透過できないので，質量流束のない境界をモデル化するために不透過境界条件を使う．

流出口で不透過境界条件を設定する．

上の境界には，種 が領域から出される流出口をモデル化するためにデフォルトの流出境界条件が陰的に適用される．

次に，既定の流束場 および任意に選ばれた種の拡散率 を使って物質輸送PDEモデルを解く．

引数"NoReaction"は，領域内に内部反応がないことを示すために使われる．

定常状態濃度場 を可視化する．

この例では，種 は速度 で右境界の活性表面に排他的に吸収されており，結果として層状の濃度場になる．

触媒コンバータ応用モデルは時間依存の物質輸送モデルである．

化学反応を伴う物質輸送

前のセクションでは化学種は化学反応を受けなかった．このセクションでは化学反応のモデリングについて説明する．

物質平衡方程式(14)および(15)の項 を使って，領域内の物質生成率()あるいは消費率()をモデル化する．物質生成あるいは物質消費を導く典型的な現象は化学反応である．例として，次の2D過渡モデルを考える．

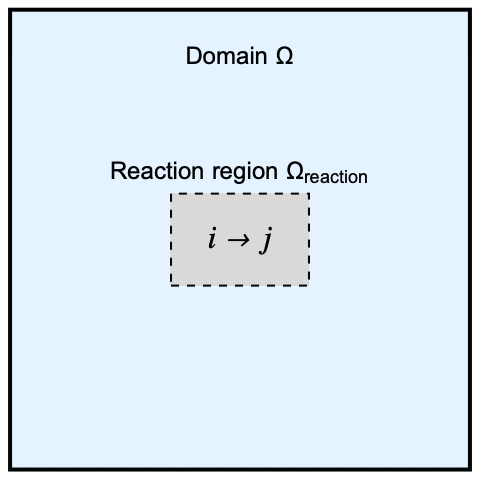
モデル領域には内部に矩形領域があり，ここで一分子反応が生じる．化学種 が自己変換して1つの分子 になるとき一分子反応という．

この例では，反応は一次反応[16]，つまり，反応物質 の物質消費速度 が反応物質自身の濃度 に比例すると想定する．

ここで は反応速度定数で，単位は である．ほとんどの化学反応では速度定数 は温度依存であり，アレニウス(Arrhenius)の式[17]で計算することができる．しかしこの例では，簡単にするために定数 を選ぶ．

通常，反応速度 が温度依存である応用例は，熱方程式が物質輸送方程式に関連付けられた連立方程式としてモデル化される．温度依存の反応速度 の設定およびそのモデリングの例は，マルチフィジックスの応用モデル熱分解で見ることができる．

速度定数 および物質消費速度 をRegionMember関数で指定する．

領域に厳密数を使うことによって，領域の帰属テストはIf文に簡約される．

化学反応の効果を強調するために，領域内に移動流れがないものと仮定する．これは物質輸送が拡散のみによるものであるということである．

物質消費速度 ，初期濃度場 ，種の拡散率 で物質輸送PDEを定義する．

種 の濃度場を秒間解く．

種 の時間依存濃度場 を可視化する．

アニメーションの質を向上させる方法はこちらをご覧いただきたい．

種 は初期濃度場 がであり，領域内で反応により徐々に消費される．そのため領域外の余分な種 が濃度勾配のため拡散によって充満する．このことでモデル領域内の全体的な濃度が低下する．

より発展した反応モデルを示す例は，触媒失活のマイクロスケールシミュレーションモデルで見ることができる．液面におけるガス吸収モデルでも見られる．

異方性物質拡散と直交異方性物質拡散

前のセクションでは，種は等方性媒体内で輸送されること，つまり，拡散物質移動の速度はその方向とは独立であり，同じ濃度勾配 によって与えられることを想定していた．しかし現実では，媒体は異方性である可能性がある．異方性拡散とは種がさまざまな方向にさまざまな速度で拡散することである．直交異方性拡散とは以下に示す通り，異方性拡散の特別な場合である．異方性挙動は自然生成物から高度な合成材料すべてに見られ，モデル化することのできる重要な現象である．

種の拡散率 が方向によって異なるため，拡散流項(18)は次のように書くことができる．

より簡約すると以下になる．

対称行列を伴う．

は拡散率テンソルである．およびはそれぞれ主拡散係数，非対角拡散係数と呼ばれる．

直交異方性拡散では，以下のグラフィックスで示されている通り，材料の種の拡散率は対称であるが主方向 ，， に沿って異なっている．非対角拡散係数はすべてゼロである．この挙動は，繊維複合材料等で見られる．拡散テンソルは次のようになる．

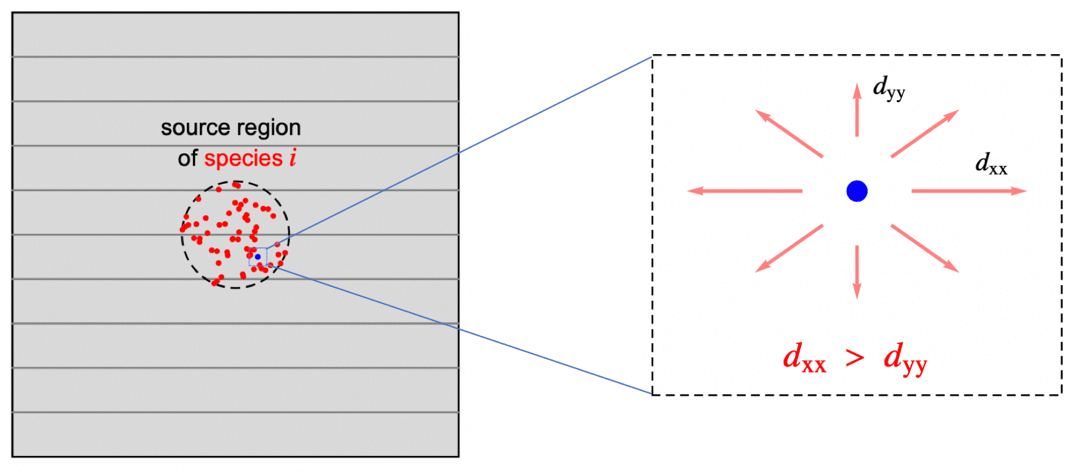
例として，層のような構造を持つ2Dの複合材料を考える．種の初期濃度はを中心とするガウスのベルカーブで記述することができる．その後種は領域全体に徐々に拡散する．

上の図は，種が灰色の線で示されている層構造の内部境界を通過する縦方向において拡散が遅くなる，直交異方性の場合を表している．拡散テンソルは次のように書くことができる．

直交異方性材料の拡散テンソル を設定する．

初期濃度場 を設定する．

種 の時間依存濃度場 を可視化する．

アニメーションの質を向上させる方法はこちらをご覧いただきたい．

種は横方向の方が早く輸送される．その結果の幅の中の濃度がより高くなる．

可変物質拡散係数

前のセクションでは，物質拡散係数と種の拡散率は，等方性媒体についての一定のスカラー か異方性媒体についての一定のテンソル のどちらかであると想定していた．しかし現実では，拡散率は温度 と種の密度 によって大きく変化する可能性がある．この両方の現象を順に見ていく．

拡散係数の温度依存性

不均一な温度場を持つ媒体における物質輸送をモデル化するとき，拡散係数 の温度依存性を説明した方がよい．初期モデルとして，拡散係数はアレニウスの式で予測することができる．

は種の拡散率，
は無限温度における種の最大拡散率，
は絶対温度，
は拡散の活性化エネルギー，
は気体定数である．

この関係の指数形式は，種の拡散率 が温度 に伴い急速に大きくなる可能性を意味する．

例として，左から右への既定の温度場の増加が である1D領域 を考える．

最大拡散率 ，活性化エネルギー ，気体定数 を設定する．

温度依存の種の拡散率を既定の温度場 で設定する．

時間 では，種は中心付近に閉じ込められており，ガウス分布で書くことができる．

を中心とするガウス分布によって，初期濃度場 を設定する．

時間依存の物質輸送PDEモデルを秒間解く．

種 の時間依存濃度場 を可視化する．

時間 において，種は中心付近に閉じ込められているが，領域全体に徐々に拡散する．右側の方が温度が高いため，種の拡散は右側の方が速い．

この例では，温度場 は既定されている．しかし，未知の温度場を持つ物質輸送モデルを解く場合，熱移動モデルと物質輸送モデルを組み合せるマルチフィジックスモデルを構築する必要がある．このように結合された熱移動物質輸送マルチフィジックス応用モデルは，モデルコレクションの熱分解の例で示してある．

拡散係数の濃度依存性

血中の薬物配送や大気中の汚染物質排出等，物質輸送の応用分野の中には，輸送された種が媒体の分子と一意の相互作用を及ぼし合うものがある[19, 20]．このような場合，拡散係数 は輸送された種濃度場 の影響を受け，非線形の物質平衡方程式になる．非保存形式の非線形物質平衡方程式は以下で与えられる．

PDEモデルの拡散係数 は濃度 自身の関数になっている．非線形拡散係数の式は通常実験的に決められ，輸送される種と媒体によって異なる．

例として，初期濃度場 ，参照拡散係数 ，濃度依存拡散係数 の1D物質輸送モデルを考える．この場合，種の拡散率 は濃度 が高くなるにつれ上昇する．

領域への種の供給をモデル化するために，左側の境界に一定の質量流束 を適用する．

濃度依存拡散係数 ，初期濃度場 ，参照拡散率 を持つ非線形物質輸送PDEを解く．

非線形性の効果をよりよく理解するために，線形の物質輸送PDEと比較する．

一定の拡散係数 を持つ線形の物質輸送PDEを設定して，それを解く．

線形モデルと非線形モデルのどちらの場合も，種は一定の質量流束 で左から領域に入った．しかし非線形モデルでは，拡散係数 が濃度 とともに増大し，それが物質輸送をスピードアップして結果的により平坦な濃度場になった．

相間物質移動

前のセクションでは，単相における物質対流と物質拡散iによる物質移動を考えた．しかし現実では，2つの異なる相が接触していたり，物質が1つの相から別の相に輸送されたりする場合が多くある．これは相間物質移動といわれる．

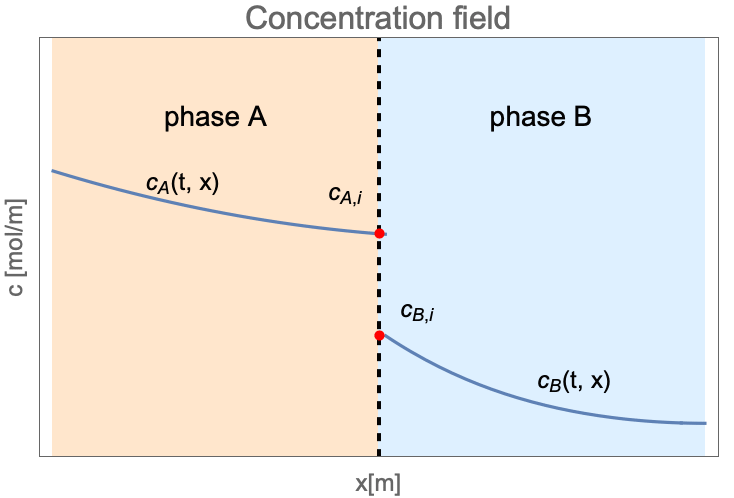
濃度場が常に連続である単相の物質移動とは異なり，種濃度は以下のように2つの状態の間の界面でジャンプすることがある．

ここで および は，相 と相 に溶けている種濃度である．下付き文字 は2つの相の界面における種濃度を表す．

相 の種濃度 と相 の種濃度 を表すために別々の物質平衡方程式を使う．

2つの相の界面において，濃度は と の間で不連続である場合がある．比 は平衡分配係数 として知られている．

係数 は圧力，温度，輸送される種の化学特性，両方の相の媒体に依存する．値 は実験的測定によって決めることができる[21]．

種の分子が2つの相の界面を素早く浸透することができると仮定すると，界面の平衡条件(22) は即座に到達され，ずっと満足される．

この仮定はWhitman [23]によりtwo-resistance theoryとして最初に提唱され，ほとんどの相間物質移動で有効である．しかし，界面で化学反応が起る場合，追加の反発力や引力が輸送される種に作用するため，この仮定は有効ではなくなる．

二酸化硫黄が大気中から水中に移動する1Dモデルを考える．相間物質移動をモデル化するために，2つの異なる相の間に薄い相間領域を定義することで，連立の架空物質源を介して平衡状態(24)を強制し，におけるの濃度の不連続性を扱うことが可能になる．

ここで相間領域の幅 を領域の長さ のになるよう設定する． の値が小さすぎると，数値的な不安定性が界面付近で起る可能性がある．

の間に薄い相間領域を持つ境界ElementMeshを作成する．

次に，気体領域，液体領域，相間領域を区別するための内部マーカーを含む完全な要素メッシュを定義する．マーカーをより明確に割り当てるために，連想を使う．

気体相および液体相のの拡散係数はそれぞれ ，で与えられる．と はそれ自身の相と相間領域内でのみ有効である．

気体相と液体相における拡散率を指定する．

2つの相の間のの移動をモデル化するために，支配物質平衡方程式(25)に結合物質源項 と を加えると，次が求まる．

ここで と はにおいて設定されるため，平衡条件(26) は界面で強制することができる．この方程式において は相間物質移動係数， は相間領域内ではオン，それ以外ではオフにするスイッチである．

相間領域内でスイッチオンにする因数を設定する．

前述のtwo-resistance theoryに基づくと，界面の平衡はすぐに達成され，ずっと維持されるものと考えられる．この条件は物質移動係数 を無限に大きく設定することでモデル化することができる．

実際では， に種の拡散率および )より何倍か大きい値を選ぶことができる．

に大きい値を設定し，相間領域全体の瞬時物質移動をモデル化する．

連立の生成項 と を設定する．

質量保存により，連立の生成項 と は同じ大きさだが符号は反対である．

領域へのの供給をモデル化するために，空気領域の左境界で一定の質量流束 を適用する．

初期濃度場 を持つ相間物質移動PDEを定義する．

気相における濃度 と液相における濃度 を記述するために，2つの物質移動モデルを定義する．

相間物質移動に対する平衡係数 の影響を調べるために，ParametricNDSolveValueで ，，において繰り返しPDEモデルを解く．

平衡係数 ，，で相間物質移動モデルを解く．

空気領域と水領域における濃度を可視化する．

平衡係数 がから逸れるにつれて，と の間のジャンプは大きくなる．

このセクションで提示しているストラテジーは，膜を通り抜ける物質移動のモデリングにも応用できる．しかしその場合は，追加の反発力（表面抵抗）が作用することもあれば，膜が平衡条件(27)に達する時間を考える必要もある．これは，膜の表面抵抗に基づいて(28)の 値を選ぶことで行える．

物質源のタイプ

体積源，層原，点源等の物質源は，熱移動モデルセクションで説明してあるのと同じようにモデル化することができる．

マルチフィジックス物質輸送

物質輸送は物理の他の分野と組み合せることができる．以下は物質輸送を使うマルチフィジックスの応用例である：

• 流体流れ
• パッシブ露凝縮器の水分凝縮

• 熱移動
• 管型反応器における放射効果
• 熱分解
• パッシブ露凝縮器の水分凝縮

• 固体力学
• 吸湿膨張

物質輸送の境界条件

物質輸送モデリングにおける最も一般的な境界条件はDirichletCondition，NeumannValue，PeriodicBoundaryConditionであり，これらは次の4つのタイプに分類できる．

• ディリクレタイプの境界条件．このタイプの境界条件は境界における種濃度 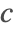を指定し，DirichletConditionでモデル化することができる．

• ノイマンタイプの境界条件．このタイプの境界条件は境界における質量流束 を指定し，NeumannValueでモデル化することができる．

• ロビンタイプの境界条件．このタイプの境界条件は境界における種濃度 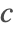とその法線微分の間の関係を指定する．ロビンタイプの境界条件は厳密に言えば一般化されたノイマン境界条件であるため，これはNeumannValueでモデル化することができる．

• 周期境界条件．このタイプの境界条件は，境界の一部における種濃度 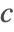が他の部分と同じになるよう指定し，PeriodicBoundaryConditionでモデル化することができる．

この4つのタイプのもと，次の境界条件を導入する．

• ディリクレタイプ
• 濃度境界条件

• ノイマンタイプ
• 質量流束境界条件
• 不透過境界条件
• 対称境界条件
• 流出境界条件

• ロビンタイプ
• Surrounding Flux境界条件

• 周期タイプ
• 周期境界条件

次のセクションでは物質輸送のモデリングでよく使われるいくつかの物理的境界条件，およびDirichletCondition，NeumannValue，PeriodicBoundaryConditionを使ってどのように表すかについて説明する．このため，現在述べている境界条件は常に例のシミュレーション領域の左側にある．例の中には追加の境界条件を右側に置いて，左側の境界条件の動作が分かりやすくなるようにしている．

ノイマンタイプの境界条件の設定は，保存モデルと非保存モデルとでわずかに異なる．この差の詳細は，以下のセクションで示す．

保存モデルおよび非保存モデルのノイマン値

前のセクションで，保存形および非保存形の物質輸送モデルの導出と設定について説明した．モデルの定式の違いはノイマンタイプの境界条件の設定方法およびその意味に影響を及ぼす．

保存形定式では，NeumannValueは の境界値を指定する．NeumannValue[val,X∈Γ_b]では次のようになる．

非保存形定式ではNeumannValueは の境界値を指定する．NeumannValue[val,X∈Γ_b]では次のようになる．

保存形の場合，境界から媒体の流れによって物質輸送される項 もノイマン値に含まれる．

提示されている境界条件の中には，ノイマン値の値を変更しなければならないものもある．例えば，方程式(29)のような保存形式のノイマン値は次のように変換しなければならない．

このような変換は問題となる．方程式(30)の左辺のようなノイマン定式は実際には計算されず方程式(31)の右辺の値で置換されるからである．一旦方程式の右辺に法線 が現れると，法線のその値は計算されなければならないがこれは自動的に行われる．境界の単位法線が単純な場合，それはモデルパラメータ"BoundaryUnitNormal"で指定することができる．これによりスピードとメモリ使用量の両方において計算効率が向上する可能性がある．

保存モデルと非保存モデルの物質輸送境界条件を示す前に，例のモデルパラメータをいくつか設定する．

モデルパラメータの設定

次のモデルパラメータは，質量輸送境界条件の例で利用される．これらのパラメータはシミュレーション領域およびシミュレーションの終了時間 を定義する．

領域とシミュレーション終了時間 のモデルパラメータを設定する．

例によっては，境界上の質量流束 あるいは濃度 等の過渡パラメータに対する時間プロファイルを既定するために，滑らかな階段関数 を使うことがある．この滑らかな階段関数は次のように定義される．

ここで関数 の最小値と最大値はそれぞれ と で表される．階段の位置は で，滑らかな傾きは で制御される．

滑らかな階段関数 を定義して可視化する．

濃度境界条件

目的

濃度境界条件の目的は特定の種濃度を境界のある部分に設定することである．

定式化

境界 上に指定された濃度 がある場合，濃度境界条件は以下によって保存モデルと非保存モデルの両方に対して与えられる．

濃度境界条件はディリクレタイプの条件であり，モデル方程式に関連付けられないので，その定式化は保存モデルでも非保存モデルでも同じである．

DirichletConditionでモデル化された，従属変数 に対する濃度境界条件．

導出

与えられた種濃度 が境界上で既定されていると，濃度境界条件のことを考える．この既定の濃度 は定数か時間依存値のいずれかである可能性があり，物質輸送PDEモデルではDirichletConditionで設定される．

例

例えば，境界上で与えられた種の供給をモデル化するためには，左端に過渡種濃度 設定することができる．右端にはノイマンのゼロ条件を流出境界として陰的に適用する．

ここで滑らかな階段関数を使って，から までの境界上における種濃度 のプロファイルを記述する．パラメータ と は，境界からの種の供給のシミュレーションのために任意に選ぶ．

滑らかな階段関数を使って，境界上の種濃度 を指定する．

次に，流束場 ，初期濃度場 ，拡散係数 の物質輸送モデルを設定する．

可視化

このシミュレーションは である不撹乱領域から始まる．濃度 が左境界で上昇すると，余分な種は右側に輸送され領域内の全体的な種濃度が上昇する．物質輸送の速度は種の拡散率 と流れ場に依存する．

流出境界条件

目的

物質輸送が流速 のシステム内で発生する場合，種が流体流とともに領域を出る流出口をモデル化するために流出境界条件を使う．

定式化

流体媒体内で物質輸送をモデル化する場合，流出口 における流出境界条件は以下で与えられる．

非保存モデルの場合，流出境界条件は実質的にノイマンのゼロ条件である．つまり，与えられた境界で境界条件が指定されていない場合，流出境界条件が陰的に適用されるのである．

導出

流体流で物質輸送をモデリングする場合，流出口の拡散質量流束はゼロに設定される．流出境界において移動された物質は質量保存だけによるもので，物質拡散 は無視されるということが確実になるようにするためである．

非保存形の定式ではNeumannValue[val,X∈Γ_b]は境界値(32) を指定する．したがって， のとき はでなければならない．非保存形式の物質輸送モデルは以下で与えられる．

保存形の定式では，NeumannValue[val,X∈Γ_b]は境界値(33) を指定する．には次が必要である．

流出境界条件は十分発達した流れにのみ適用することができる．つまり，流出口で速度プロファイル は流れの方向を変更しないのである．

流出境界からの再循環は乱流でよく起るが，再循環がある場合，再流入する流れは領域内部の流れの濃度場に影響を与え，ゼロ拡散流束の仮定を破る．このような状態では，流出境界条件はもう適用できない．

例

次の例では，流出境界条件を左端に設定して，領域から流出する質量流束をモデル化する．保存モデルと非保存モデルの両方に対する境界条件の設定を示す．

流出境界の効果を強調するために，種の拡散率 をゼロと仮定する．したがって物質輸送は流体流 の対流のみによるものである．

領域への右側からの種の供給をモデル化するために，濃度境界条件を使う．

次に保存モデルと非保存モデルの両方に対する境界条件の設定を示す．保存モデル形式を加える以外，以下に示す両方の設定は同じである．

流出境界条件を持つ保存形式の物質輸送モデル

流出口で左に向かう流れ および法線 を持つ保存形式の物質輸送モデル対する流出境界条件を設定する．

このPDEモデルが対流優勢であることを示すメッセージが生成される．この場合拡散質量流束がないため，メッセージが出るのは想定通りである．この問題についての情報は有限要素使用のヒントチュートリアルに記載されている．

流出境界条件を持つ非保存形式の物質輸送モデル

境界のどの部分にも境界条件が指定されていない場合，デフォルトではノイマンのゼロ条件が陰的に使われる．これは流出境界が非保存形式の物質輸送モデルに使われるデフォルトの境界条件であることを意味する．

流出境界条件の可視化

流出境界条件を左境界に適用すると，種は流体流によって反射なしで領域から輸送された．保存モデルと非保存モデルの結果は一致していることが分かる．

質量流束境界条件

目的

質量流束境界条件の目的は，与えられた種が境界のある部分から流入または流出する量をモデル化することである．

定式化

既定の質量流束 が境界 上にある場合，質量流束境界条件は以下で与えられる．

導出

境界に垂直な質量流束 が指定されており，ゼロではない境界は質量流束境界と呼ばれる．

慣習により， の前に負記号を加え，質量流束が外向きの法線 と逆向きに指定されていることを示す．したがって， の正値は，指定された種が領域に入る内向きの質量流束を示し，負の は外向きの流束を示す．

前のセクション輸送方程式の導出で述べたように，質量流束 は拡散流束 と対流流束 からなる．

保存形の定式の場合，NeumannValue[val,X∈Γ_b]は境界値(34) を指定するということをを先に述べた．したがって，(35)を(36)に挿入すると，保存モデルに対する質量流束境界条件は次で与えられる．

この場合 は であり，NeumannValue[(t,X),X∈Γ_b]となる．

非保存形の定式では，NeumannValue[val,X∈Γ_b]は境界値(37) を指定する．よって，(38)の境界対流流束 を右辺に代入すると，非保存モデルに対する質量流束境界条件は次で与えられる．

質量流束 の単位は，境界の次元に依存する．1D ()，2D ()，3D ()の領域では， の単位はそれぞれ，，である．

例

次の例では，左境界に過渡質量流束 を適用して，実際の化学反応が関与せずに，種が領域内に供給されるのをモデル化する．右境界を流出境界条件として設定し，右端で流出する質量流束をモデル化する．

質量流束のプロファイルは次のように定義される．

次に保存モデルと非保存モデルの両方の境界条件を設定する．保存モデル形式を加える以外，以下に示す両方の設定は同じである．

質量流束境界条件を持つ保存物質輸送モデル

ここで流れ場 および流出境界条件を指定して，右端の流出質量流束をモデル化する．

初期濃度場と拡散係数は，それぞれ ，で与えられる．

質量流束境界条件を持つ非保存物質輸送モデル

流出口における流速が ，法線が である非保存物質輸送モデルの流束境界条件を設定する．

非保存モデルでは，流出境界条件はノイマンのゼロ条件であり，領域の右端で陰的に適用される．

質量流束境界条件の可視化

質量流束 を左境界で適用すると，種は徐々に領域内に輸送される．質量流束が時間 でオフになった後，残りの種は引き続き流体流束とともに領域から輸送され，全体的な濃度場が縮小される．保存モデルと非保存モデルの結果は一致している．

不透過境界条件

不透過境界条件は，境界全域の流束が である場合の質量流束境界条件の特殊系である．

目的

不透過境界条件は，種が通過できないため質量流束が存在しない境界をモデル化するものである．

定式化

不透過境界条件は以下で与えられる．

保存モデルでは，不透過境界条件は実質的にノイマンのゼロ条件であり，指定された境界で境界条件が指定されていないときに陰的に適用される．

導出

不透過境界条件は質量流束が存在しない境界を表す．

(39)を質量流束境界条件(40)に挿入すると，保存モデルと非保存モデル両方の不透過境界条件の定式化が得られる．

例

次の例ではガウス分布を使って領域内の初期濃度場 を記述する．不透過境界を両側に置いて，境界の質量流束を阻止する．

ガウス分布を初期濃度場 として設定する．

不透過境界の効果を強調するために，流れ場を と仮定する．つまり物質輸送は拡散にのみよるものである．種の拡散係数は で与えられる．

次に保存モデルと非保存モデル両方の境界条件を示す．保存モデル形式を加える以外，以下に示す両方の設定は同じである．

不透過境界条件を持つ保存物質輸送モデル

境界のどの部分にも境界条件が指定されていない場合，デフォルトではノイマンのゼロ条件が陰的に適用される．つまり，不透過境界は保存物質輸送モデルに使われるデフォルトの境界条件であることを意味する．

ここで流出境界条件も適用して，右端の流出質量流束をモデル化する．

不透過境界条件を持つ非保存物質輸送モデル

不透過境界条件の可視化

両方のモデルで および における正味濃度を計算する．

初期濃度場は内部拡散により徐々に平坦化されたが，領域内の正味濃度は変化していないことが分かる．これは両端の不透過境界に質量流束がないためである．保存モデルと非保存モデルの結果は一致している．

周囲流束境界条件

周囲流束境界条件は，流速場がゼロ のときという特殊な場合に適用される流束条件である．したがって，周囲流束境界条件は，境界の流束が外部濃度 および による物質移動係数 に依存する場合の質量流束境界条件を拡張するものである．

目的

周囲流束境界条件は，モデル化されたシステムと，流速がゼロ である境界の拡散を介した周囲環境の間の物質移動をモデル化するために使う．

定式化

外部濃度 と境界 上の物質移動係数 のプロファイルが与えられると，周囲流束境界条件は以下で与えられる．

このモデルには流体流束 が関与していないため，周囲流束境界条件の定式化は保存モデルと非保存モデルの両方で同じである．

NeumannValueでモデル化された従属変数 の周囲流束境界．

導出

協会に流体流束がない場合，種が境界を通過するための唯一のメカニズムは拡散である．境界の拡散流束速度は濃度勾配，輸送される種の物理特性，媒体の特性（相や密度等）に依存する．

残念ながら拡散流束と，このような物理特性の間の関係は簡単には決定できない．これに対処するために，物質移動係数 を定義し，これらの要因をまとめる．拡散質量流束は以下のように表すことができる．

ここで はモデル化された領域の周囲における外部濃度である．物質移動係数 実験的に決定することができる[41, 42]．物質移動係数 は通常，気体相ではの範囲，流体相ではの範囲である．

(43)を質量流束境界条件(44)に挿入し，流れ場 を設定すると，周囲流束境界条件は次のように書くことができる．

例

Consider a 1D example where 二酸化炭素が領域の左と右の境界から拡散して出る1Dの例を考える．領域の外側の濃度は同程度に薄く，と想定される．境界を通過する拡散質量流束は，与えられた物質移動係数 の周囲流束境界条件によってモデル化される．

この場合，ガウス分布を使って内部濃度場 を記述する．の拡散係数は で与えられる．

境界上で外部濃度 および物質移動係数 を指定する．

周囲流束境界の効果をよりよく理解するために，境界条件を持たない解析解の結果と比較する．つまり，分子は無限範囲の領域を持つかのように拡散し続けるのである．

周囲流束境界条件の可視化

周囲流束条件を両端に適用すると，分子は境界条件がないときよりも速い速度で領域から移動して出て行く．これは境界における物質拡散が，この場合，内部拡散よりも効率的であることを意味している．

周囲環境への拡散流束は場合によって異なり，外部濃度 および物質移動係数 によって制御される．

と における正味濃度 を比較する．

周囲流束条件があると，正味濃度は3時間で約からまで減少する．

対称境界条件

目的

対称境界条件は，実質的に，境界に垂直な流速がゼロであるシミュレーション領域の線形境界を反映することによって，計算領域の範囲を完全な物理的モデル形状の対称サブ領域に減少させるために使われる．これにより少ないメモリで解を速く処理することができる．

定式化

対称境界条件は以下で与えられる．

対称境界条件の定式化は保存モデルでも非保存モデルでも同じである．対称境界の法線流速 はずっとゼロで維持されるため，(45)には境界対流流束項 がない．

NeumannValueでモデル化された，従属変数 の対称境界．

対称境界条件は実質的にノイマンのゼロ条件であるため，与えられた境界で境界条件が指定されていない場合は，ノイマンのゼロ条件が陰的に適用される．

導出

線形境界全体で対称性を維持するためには，常に境界に垂直な質量流束 および流れ があってはならない．

(46)を質量流束境界条件(47)に挿入すると，周囲流束境界条件は次のように書くことができる．

例

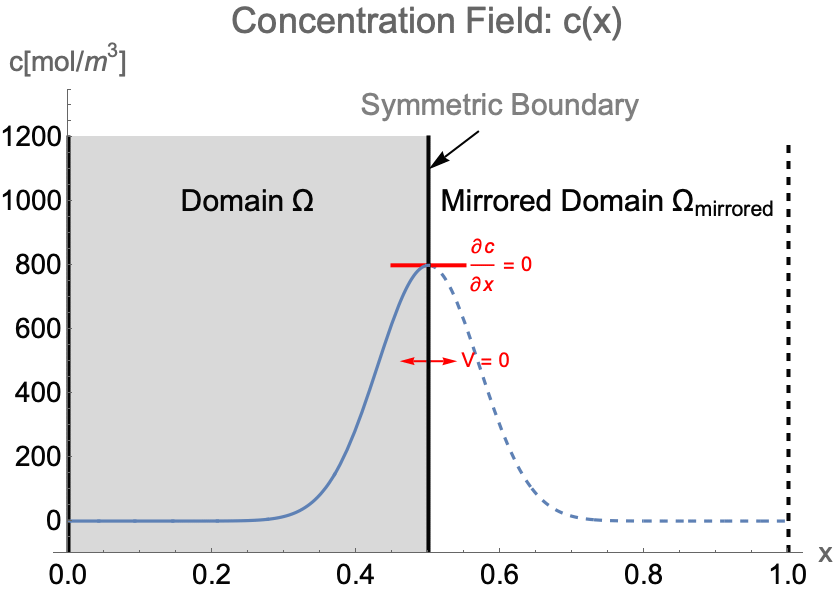
1Dシステムの濃度場を から まで解く場合を考える．濃度パターンが に沿って鏡面対称であると想定される場合，システムの左半分だけでシミュレーション領域を構築することができる．その後 で対称境界条件を適用しなければならない．

対称性のため，対称境界の濃度勾配 および流速 は常にゼロのままである．厳密に言うと，対称境界は実際には不透過境界である．不透過境界条件(48)で流速 をゼロに設定することにより，対称境界条件は次のように書くことができる．

周期境界条件

目的

周期境界条件の目的は，領域の周期性を使うために，種濃度をある境界から別の境界にマップすることである．

定式化

種濃度 を周期境界 から目的の境界にマップする関数 が与えられると，周期境界条件は次のように書くことができる．

周期境界の定式化は， 保存モデルでも非保存モデルでも同じである．

PeriodicBoundaryConditionでモデル化された，従属変数 の周期境界条件．

導出

周期境界条件は，空間的に周期的な領域における物質移動を計算するために適用する．目標の境界が与えられると，周期境界の種濃度 は既定の関数 によって目標表面上の濃度 にマップすることができる．境界条件は，物質輸送PDEモデルのPeriodicBoundaryConditionで設定される．

例

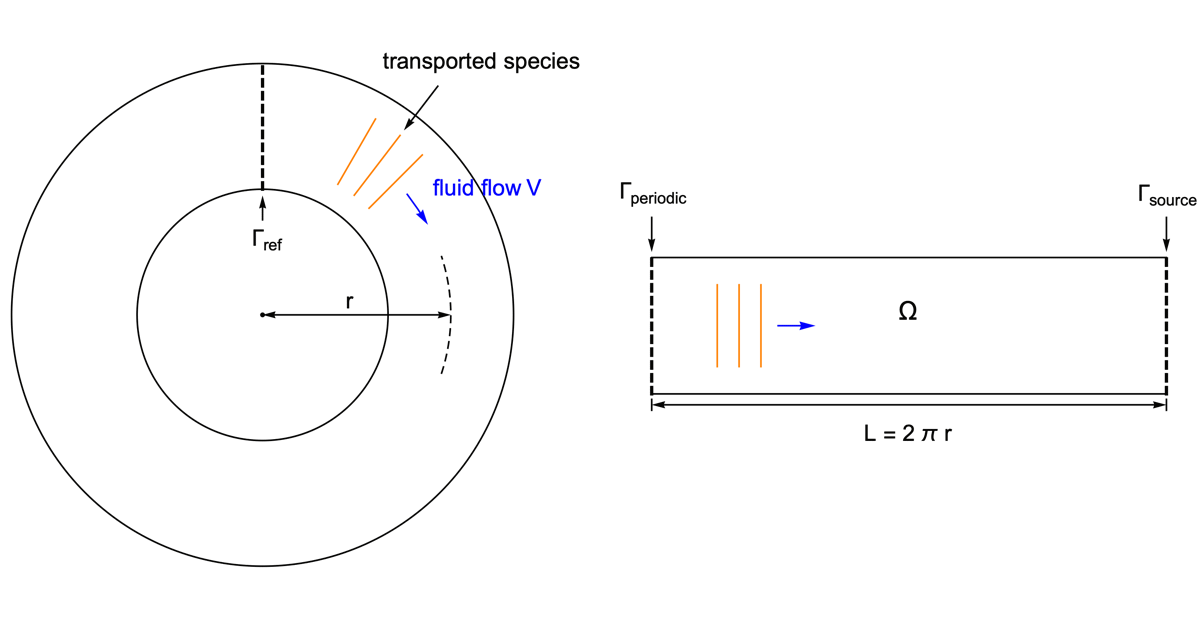
例として，円管内の種の輸送を見る．周期境界条件の使用法では，1D領域でシミュレーションを行うことが可能である．

周期境界の効果を強調するために，種の拡散率 をゼロと想定する．したがって種の輸送は流体流れ の対流のみによるものである．

モデル変数，種の拡散率 ，流速 を設定する．

円管は管の円周に等しい長さ の1Dモデルに変換される．周期境界は左端で設定されるため，種が領域の右側を通過するとき，左側で同じ大きさで再び現れる．

マッピング関数 で左端でPeriodicBoundaryConditionを設定する．

次に初期濃度場 としてガウス分布を使う．

初期濃度場 を設定する．

このPDEモデルが対流支配下にあることを表すメッセージが生成される．この場合は拡散質量流束がないため，メッセージは想定通りである．この問題についての情報は有限要素の使用法のヒントチュートリアルに記載されている．

周期境界条件の可視化

種は，空間的に周期的な領域内の流体流れによって右に輸送されたことが分かる．種が右の境界を通過すると，それは左側にまた現れる．これは周期境界条件で設定されたこの領域の周期性のためである．種の拡散率はゼロに設定されており，物質は対流によってのみ輸送されるので，種濃度のパターンと大きさは常に一定のままである．

付録

物質平衡方程式の特別な場合

物質平衡方程式の導出のセクションで示した通り，物質平衡方程式の保存形と非保存形は次で与えられる．

以下のセクションでは物質平衡方程式の特別な場合と，それが円筒座標および球座興でどのように表せるかを示す．

定常の場合

濃度場が定常状態にある場合，物質平衡方程式(49)および(50)の過渡項は消失し，物質平衡方程式は以下のように簡約される．

拡散のみによる物質輸送

物質輸送が固体媒体で生じる場合，定義上固体は内部速度場 を持たないため，物質平衡方程式(51)および(52)の対流項はゼロに設定され，以下が得られる．

この場合，物質輸送は拡散でのみ生じる．

対流のみによる物質輸送

流体流れによる物質輸送をモデル化する場合，物質輸送が物質対流convection,tによって支配されているならば拡散項は無視でき，以下が得られる．

この場合，物質輸送は対流によってのみ起る．

対流成分および が大きくなる場合，物質輸送モデルは対流支配下のPDEになる．このタイプのPDEの解は不安定になる可能性があるため，追加の安定化方法が必要になることがある．この問題についての情報は有限要素の使用のヒントチュートリアルに記載されている．

円筒座標系における物質平衡方程式

物質輸送問題をモデル化する場合，モデルを直交座標で記述するのは便利ではないことがある．熱方程式も円筒座標系あるいは球座標系を使って表すことができる．

円筒座標系を示すグラフィックス．

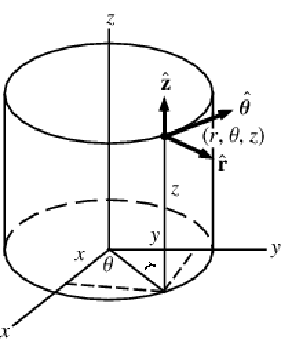
円筒座標系では，，， はそれぞれ動径，周方向，軸方向を表す．直交座標系では，円筒座標系は次のように定義される．

あるいは以下である．

座標関係(53)を方程式(54)および(55)に代入することによって，物質平衡方程式は以下のように円筒座標系で表すことができる．

モデル内の物質輸送が 軸について回転対称ならば，結果の濃度場 は 方向では不変である．よって，方程式(56)は次のように簡約される．

この場合，この対称特性を使って3D物質輸送問題を2D領域でモデル化することができる．このタイプのモデルは軸対称モデルとして知られている．

球座標系における物質平衡

球座標系を示すグラフィックスである．

球座標系では，，， はそれぞれ動径，方位角，極方向を表す．直交座標系では，極座標系は以下のように定義される．

あるいは次のようになる．

座標関係(57)を方程式(58)および(59)に挿入すると，物質平衡方程式は球座標系で以下のように表すことができる．

用語集

参考文献

1.  Fick, A. Über Diffusion. Annalen der Physik (in German), 94 (1): 59–86 (1855).

2.  Wolf, E. E. and Alfani, F. Catalysts Deactivation by Coking, Catalysis Reviews: vol 24 329-371 (1982).

3.  Calvo, E. G., Arranz, M. A. and Leton, P. Effects of Impurities in the Kinetics of Calcite Decomposition, Thermochimica Acta. 170: 7–11 (1990).

4.  Fu, J. C., Hagemeir, C. and Moyer, D. L., An unified mathematical model for diffusion from drug polymer composite tablets, Journal of Biomedical Materials Research: vol. 10, no. 5, pp. 743–758 (1976).

5.  Parra-Guevara, D. and Skiba, Y. N. Elements of the mathematical modeling in the control of pollutants emissions, Ecological Modelling: vol. 167, no. 3, pp. 263–275 (2003).

6.  Goldstein, R.J. and Cho, H. H. A review of mass transfer measurements using naphthalene sublimation, Experimental Thermal and Fluid Science: vol. 10, no. 4, pp. 416–434 (1995).

7.  Cañizares, P., García-Gómez, J., Fernández de Marcos, I., Rodrigo, M. A. and Lobato, J. Measurement of Mass-Transfer Coefficients by an Electrochemical Technique, Journal of Chemical Education: vol. 83, no. 8 (2006).

8.  LeVeque, R. J. Numerical Methods for Conservation Laws, Birkhduser (1992).

9.  Whitman, G. Walter. The two film theory of gas absorption, International Journal of Heat and Mass Transfer: vol. 5, no. 5, pp. 429-433 (1962).

10.  Prausnitz, J. M., Lichtenthaler R. N. and de Azevedo, E. G. Molecular Thermodynamics of Fluid Phase Equilibria 3rd Ed., Prentice Hall PTR, New Jersey (1999).