AnglePath3D

AnglePath3D[{{α1,β1,γ1},{α2,β2,γ2},…}]

gives the list of 3D coordinates of a path of an object that starts at {0,0,0}, then takes a series of steps of unit length, each in the direction of the axis obtained after successive rotation of the object by the Euler angles αi, βi, γi.

AnglePath3D[{{α1,β1},{α2,β2},…}]

assumes the Euler angles γi to be 0.

AnglePath3D[{mat1,mat2,…}]

takes the successive rotations to be specified by the 3D rotation matrices mati.

AnglePath3D[{{r1,rot1},{r2,rot2},…}]

takes successive steps of length ri with Euler angles or rotation matrices specified by roti.

AnglePath3D[{x0,y0,z0},steps]

starts at the point {x0,y0,z0}.

AnglePath3D[{rot0},steps]

starts in the axis direction specified by rotating the object according to Euler angles or rotation matrix rot0.

AnglePath3D[{{x0,y0,z0},rot0},steps]

starts at point {x0,y0,z0} with the axis direction specified by rot0.

AnglePath3D[init,steps,form]

returns at each step the data of the form specified by form.

Details and Options

  • The successive directions taken in AnglePath3D are defined by the 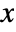axes of successive local frames, which can be thought of as defining the orientation of a 3D object.
  • By default, the orientation of the initial frame is aligned with the coordinate axes.
  • At each step, the local frame is rotated, then the path advances by the specified distance along the 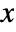axis in the new frame.
  • A triple of angles {αi,βi,γi} is generally equivalent to the Euler rotation matrix EulerMatrix[{αi,βi,γi},{3,2,1}]. In this convention, αi can be thought of as a longitude angle, βi as a latitude angle and γi as a rotation angle about the displacement axis.
  • The lengths of the steps can be specified with {{r1,rot1},{r2,rot2},…}, or equivalently with {{r1,r2,…},{rot1,rot2,…}}.
  • For a step of length ri with direction specified by mati, the next position pi={xi,yi,zi} is obtained by pi=pi-1+fi.{ri,0,0}, with the frame rotation matrix fi given by fi=fi-1.mati and f0=mat0.
  • AnglePath3D[steps,form] is equivalent to AnglePath3D[{0,0,0},steps,form].
  • Possible choices for form in AnglePath3D[…,form] include:
  • "Position"Cartesian coordinates {xi,yi,zi} (default)
    "FrameMatrix"rotation matrix of the frame fi with respect to f0
    "EulerMatrix"rotation matrix of the frame fi with respect to fi - 1
    "FrameAngles"EulerAngles[fi,{3,2,1}]
    "EulerAngles"{αi,βi,γi}
    "Translation"TranslationTransform[{xi,yi,zi}]
    "Rotation"AffineTransform[fi]
    "RotationTranslation"AffineTransform[{fi,{xi,yi,zi}}]
    {form1,form2,…}a list of forms
  • The arguments init and steps can be symbolic. They can also be Quantity objects.
  • AnglePath3D has the option WorkingPrecision, which determines the precision of numbers generated.
  • With the default setting WorkingPrecisionAutomatic, exact numbers will be generated for exact input only for fairly short paths; for longer paths, machine precision will be used.

Examples

open allclose all

Basic Examples  (6)

Starting at {0,0,0} along the axis, move several unit steps, rotating by 90° with respect to the local axis at each step:

Move several unit steps, rotating the local frame by Euler angles 30°, 30° and 90° with respect to the local axes , and :

Move with steps of different lengths, rotating the local frame by Euler angles 90° with respect to the local axes and :

Advance 20 steps, always rotating the local frame by Euler angles 100° with respect to all axes:

Draw a helix:

Generate the transformation functions of a path:

Apply them to a triceratops:

Use symbolic inputs:

Scope  (22)

Steps Specification  (7)

Generate a path of unit steps with triples of Euler angles, starting at position {0,0,0} in the direction of the axis:

Generate a path of unit steps with pairs of Euler angles:

AnglePath3D[{{α1,β1},{α2,β2},…}] assumes the third Euler angles to be 0:

Specify the lengths of the steps:

The lengths and directions of the steps can be given jointly or separately:

Use three-dimensional rotation matrices instead of Euler angles:

Use Quantity objects in input:

Path Initialization  (7)

Generate a path starting at a specific position:

Choose the orientation of the initial frame by giving a triple of Euler angles:

Specify the initial orientation with a pair of Euler angles:

Specify the initial orientation with a three-dimensional rotation matrix:

Generate a path where both initial position and initial orientation are specified:

The orientation of the initial frame can be alternatively specified at the first step:

These are two equivalent paths:

Use Quantity objects in input:

Forms of Data  (8)

By default, AnglePath3D returns the position of the point reached at each step:

Compute the orientation of each local frame with respect to the previous local frame:

Compute the orientation of each local frame with respect to the global frame:

Compute the Euler angles determining the orientation of each local frame in the global frame:

Generate translation transformations from the initial position:

Apply them to an ellipsoid:

Generate rotation transformations with respect to the initial frame:

Apply them to an ellipsoid:

Generate rotation-translation transformations from the initial step:

Apply them to an ellipsoid:

Produce different forms of data with one AnglePath3D call:

The first elements of the triples are the Euler rotations with respect to the previous frame:

The second elements are the positions:

The third elements are the transformations from the initial frame:

Options  (1)

WorkingPrecision  (1)

By default, AnglePath3D with exact input gives exact numbers for short paths and machine numbers for long paths:

Specify infinite working precision to perform exact, but slower, computations:

Use any specified precision for the computations:

Applications  (7)

Path Visualization of a Pointlike Object  (5)

Draw a hexagon in the - plane:

Draw an octagon in the - plane:

Visit all vertices of a cube once:

Draw a three-dimensional spiral:

Make a random walk where successive steps change direction by at most 20° in any Euler angles:

Make a random walk where successive steps change direction by Euler angles between 0 and :

Path Visualization of a Rigid Body  (2)

Visualize the orientation of a rigid body after successive rotations about a same axis:

About the axis:

Generate the position reached at each step at the same time:

About the axis:

About the axis:

Fly to all vertices of a cube once:

Follow the same directions but with different orientations:

Properties & Relations  (5)

AnglePath3D[{{θ1,0,0},{θ2,0,0},…}] returns a path in the - plane:

The generated path is equivalent to that of AnglePath[{θ1,θ2,…}]:

Specifying Euler angles is equivalent to specifying -- Euler matrices:

Specifying initial Euler angles is equivalent to specifying an initial -- Euler matrix:

Global frame rotations can be obtained as multiplications of all previous relative Euler rotations:

Compute the positions for a path with the following inputs:

An alternative way to compute these positions is using the form "FrameMatrix":

Interactive Examples  (1)

Neat Examples  (3)

Animate a shuttle looping in the - plane:

Wolfram Research (2017), AnglePath3D, Wolfram Language function, https://reference.wolfram.com/language/ref/AnglePath3D.html (updated 2019).

Text

Wolfram Research (2017), AnglePath3D, Wolfram Language function, https://reference.wolfram.com/language/ref/AnglePath3D.html (updated 2019).

CMS

Wolfram Language. 2017. "AnglePath3D." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/AnglePath3D.html.

APA

Wolfram Language. (2017). AnglePath3D. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AnglePath3D.html

BibTeX

@misc{reference.wolfram_2024_anglepath3d, author="Wolfram Research", title="{AnglePath3D}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/AnglePath3D.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_anglepath3d, organization={Wolfram Research}, title={AnglePath3D}, year={2019}, url={https://reference.wolfram.com/language/ref/AnglePath3D.html}, note=[Accessed: 05-November-2024 ]}