AnglePath3D
AnglePath3D[{{α1,β1,γ1},{α2,β2,γ2},…}]
给出一个对象从 {0,0,0} 开始,按欧拉角 αi、βi、γi 连续转动获得的 ![]() 轴方向,每次前进单位长度所得路径的三维坐标列表.
轴方向,每次前进单位长度所得路径的三维坐标列表.
AnglePath3D[{{α1,β1},{α2,β2},…}]
假定欧拉角 γi 为 0.
AnglePath3D[{mat1,mat2,…}]
按三维旋转矩阵 mati 指定的进行转动.
AnglePath3D[{{r1,rot1},{r2,rot2},…}]
前进长度依照 ri,欧拉角或旋转矩阵由 roti 指定.
AnglePath3D[{x0,y0,z0},steps]
从点 {x0,y0,z0} 开始.
AnglePath3D[{rot0},steps]
从由欧拉角或旋转矩阵 rot0 指定的 ![]() 轴方向开始.
轴方向开始.
AnglePath3D[{{x0,y0,z0},rot0},steps]
从点 {x0,y0,z0} 开始,由 rot0 指定 ![]() 轴方向.
轴方向.
AnglePath3D[init,steps,form]
用 form 指定的形式返回每一步的数据.
更多信息和选项


- AnglePath3D 中连续转动的方向由连续的局部标架的
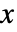 轴定义,可将其视为定义三维物体的朝向.
轴定义,可将其视为定义三维物体的朝向. - 缺省情况下,初始标架的朝向与坐标轴对齐.
- 在每一步中,局部标架被旋转,路径向前沿新的标架中的
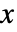 轴前进指定的距离.
轴前进指定的距离. - 通常,三个角 {αi,βi,γi} 与欧拉旋转矩阵 EulerMatrix[{αi,βi,γi},{3,2,1}] 等价. 按照该约定,αi 可被视为经度角,βi 为纬度角,γi 为关于位移轴的旋转角.
- 可以用 {{r1,rot1},{r2,rot2},…} 来指定步长,或用 {{r1,r2,…},{rot1,rot2,…}} 来指定.
- 对于由 mati 指定方向的步长 ri,通过 pi=pi-1+fi.{ri,0,0} 来得出下一个位置 pi={xi,yi,zi},其中,标架旋转矩阵 fi 由 fi=fi-1.mati 和 f0=mat0 给出.
- AnglePath3D[steps,form] 等价于 AnglePath3D[{0,0,0},steps,form].
- 在 AnglePath3D[…,form] 中,form 的可能选择包括:
-
"Position" 直角坐标 {xi,yi,zi}(默认) "FrameMatrix" 标架 fi 相对于 f0 的旋转矩阵 "EulerMatrix" 标架 fi 相对于 fi - 1 的旋转矩阵 "FrameAngles" EulerAngles[fi,{3,2,1}] "EulerAngles" {αi,βi,γi} "Translation" TranslationTransform[{xi,yi,zi}] "Rotation" AffineTransform[fi] "RotationTranslation" AffineTransform[{fi,{xi,yi,zi}}] {form1,form2,…} 格式列表 - 参数 init 和 steps 可以为符号. 它们也可以是 Quantity 对象.
- AnglePath3D 有一个 WorkingPrecision 选项,确定了生成数字的精度.
- 采用默认设置 WorkingPrecisionAutomatic 的情况下,只为相当短的路径的精确输入生成精确数字;对于较长的路径,将使用机器精度.
范例
打开所有单元关闭所有单元基本范例 (6)
范围 (22)
步进指定 (7)
产生具有三个欧拉角的单位步长路径,从位置 {0,0,0} 开始,方向为 ![]() 轴:
轴:
AnglePath3D[{{α1,β1},{α2,β2},…}] 假定第三个欧拉角为 0:
在输入中使用 Quantity 对象:
路径初始化 (7)
在输入中使用 Quantity 对象:
数据格式 (8)
默认情况下,AnglePath3D 返回每个步骤到达点的位置:
用一个 AnglePath3D 命令产生不同格式的数据:
选项 (1)
WorkingPrecision (1)
应用 (7)
属性和关系 (5)
AnglePath3D[{{θ1,0,0},{θ2,0,0},…}] 返回位于 ![]() -
-![]() 平面上的路径:
平面上的路径:
所产生的路径等价于 AnglePath[{θ1,θ2,…}] 所产生的路径:
互动范例 (1)
文本
Wolfram Research (2017),AnglePath3D,Wolfram 语言函数,https://reference.wolfram.com/language/ref/AnglePath3D.html (更新于 2019 年).
CMS
Wolfram 语言. 2017. "AnglePath3D." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2019. https://reference.wolfram.com/language/ref/AnglePath3D.html.
APA
Wolfram 语言. (2017). AnglePath3D. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/AnglePath3D.html 年