gives the arc secant in degrees of the complex number ![]() .
.




ArcSecDegrees
gives the arc secant in degrees of the complex number ![]() .
.
Details

- ArcSecDegrees, along with other inverse trigonometric and trigonometric functions, is studied in high-school geometry courses and is also used in many scientific disciplines.
- All results are given in degrees.
- For real
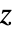 outside the interval
outside the interval 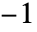 to
to 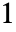 , the results are always in the range
, the results are always in the range 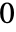 to
to 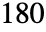 , excluding
, excluding 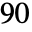 .
. - ArcSecDegrees[z] returns the angle
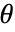 in degrees for which the ratio of the hypotenuse to the adjacent side of a right triangle is
in degrees for which the ratio of the hypotenuse to the adjacent side of a right triangle is 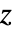 .
. - For certain special arguments, ArcSecDegrees automatically evaluates to exact values.
- ArcSecDegrees can be evaluated to arbitrary numerical precision.
- ArcSecDegrees automatically threads over lists.
- ArcSecDegrees[z] has a branch cut discontinuity in the complex
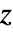 plane running from
plane running from 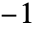 to
to 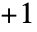 .
. - ArcSecDegrees can be used with Interval, CenteredInterval and Around objects.
- Mathematical function, suitable for both symbolic and numerical manipulation.
Examples
open all close allBasic Examples (7)
Calculate the angle BAC of this right triangle:
The numerical value of this angle:
Solve an inverse trigonometric equation:
Solve an inverse trigonometric inequality:
Apply ArcSecDegrees to the following list:
Plot over a subset of the reals:
Asymptotic expansion at Infinity:
Scope (37)
Numerical Evaluation (6)
The precision of the output tracks the precision of the input:
Evaluate for complex arguments:
Evaluate ArcSecDegrees efficiently at high precision:
Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:
Or compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix ArcSecDegrees function using MatrixFunction:
Specific Values (5)
Values of ArcSecDegrees at fixed points:
Simple exact values are generated automatically:
Zero of ArcSecDegrees:
Visualization (4)
Plot the ArcSecDegrees function:
Plot over a subset of the complexes:
Plot the real part of ArcSecDegrees:
Plot the imaginary part of ArcSecDegrees:
Polar plot with ArcSecDegrees:
Function Properties (10)
ArcSecDegrees is defined for all real values except from the interval ![]() :
:
ArcSecDegrees achieves all real values from the interval ![]() except
except ![]() :
:
ArcSecDegrees is not an analytic function:
ArcSecDegrees is monotonic in a specific range:
ArcSecDegrees is injective:
ArcSecDegrees is not surjective:
ArcSecDegrees is non-negative on its real domain:
It has both singularity and discontinuity for x in [-1,1]:
ArcSecDegrees is neither convex nor concave:
ArcSecDegrees is concave for x in [1,∞):
TraditionalForm formatting:
Integration (2)
Series Expansions (4)
Find the Taylor expansion using Series:
Plot the first three approximations for ArcSecDegrees around ![]() :
:
Find series expansions at branch points and branch cuts:
Asymptotic expansion at a singular point:
ArcSecDegrees can be applied to power series:
Function Identities and Simplifications (2)
Simplify expressions involving ArcSecDegrees:
Use TrigToExp to express through logarithms and square roots:
Function Representations (1)
Represent using ArcCosDegrees:
Applications (6)
Solve inverse trigonometric equations:
Solve an inverse trigonometric equation with a parameter:
Use Reduce to solve inequalities involving ArcSecDegrees:
Numerically find a root of a transcendental equation:
Plot the function to check if the solution is correct:
Plot the real and imaginary parts of ArcSecDegrees:
Different combinations of ArcSecDegrees with trigonometric functions:
Properties & Relations (6)
Compositions with the inverse trigonometric functions:
Use PowerExpand to disregard multivaluedness of the ArcSecDegrees:
Alternatively, evaluate under additional assumptions:
Use FunctionExpand to convert trigs of arctrigs into an algebraic function:
This shows the branch cut of the ArcSecDegrees function:
ArcSecDegrees gives the angle in degrees, while ArcSec gives the same angle in radians:
FunctionExpand applied to ArcSecDegrees generates expressions in trigonometric functions in radians:
ExpToTrig applied to the outputs of TrigToExp will generate trigonometric functions in radians:
Neat Examples (2)
Solve trigonometric equations involving ArcSecDegrees:
Numerical value of this angle in degrees:
Plot ArcSecDegrees at integer points:
See Also
Tech Notes
Related Guides
History
Text
Wolfram Research (2024), ArcSecDegrees, Wolfram Language function, https://reference.wolfram.com/language/ref/ArcSecDegrees.html.
CMS
Wolfram Language. 2024. "ArcSecDegrees." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ArcSecDegrees.html.
APA
Wolfram Language. (2024). ArcSecDegrees. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ArcSecDegrees.html
BibTeX
@misc{reference.wolfram_2025_arcsecdegrees, author="Wolfram Research", title="{ArcSecDegrees}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/ArcSecDegrees.html}", note=[Accessed: 09-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_arcsecdegrees, organization={Wolfram Research}, title={ArcSecDegrees}, year={2024}, url={https://reference.wolfram.com/language/ref/ArcSecDegrees.html}, note=[Accessed: 09-January-2026]}