ArgMin
ArgMin[f,x]
gives a position xmin at which f is minimized.
ArgMin[f,{x,y,…}]
gives a position {xmin,ymin,…} at which f is minimized.
ArgMin[{f,cons},{x,y,…}]
gives a position at which f is minimized subject to the constraints cons.
ArgMin[…,x∈rdom]
constrains x to be in the region or domain rdom.
Details and Options


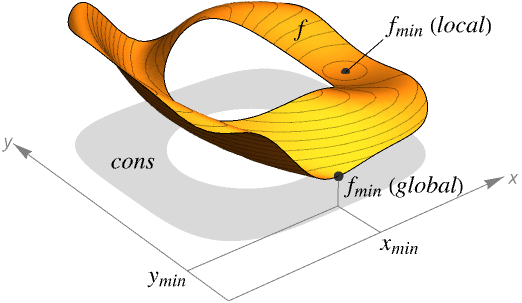
- ArgMin finds the global minimum of f subject to the constraints given.
- ArgMin is typically used to find the smallest possible values given constraints. In different areas, this may be called the best strategy, best fit, best configuration and so on.
- If f and cons are linear or polynomial, ArgMin will always find a global minimum.
- The constraints cons can be any logical combination of:
-
lhs==rhs equations lhs>rhs, lhs≥rhs, lhs<rhs, lhs≤rhs inequalities (LessEqual,…) lhsrhs, lhsrhs, lhsrhs, lhsrhs vector inequalities (VectorLessEqual,…) Exists[…], ForAll[…] quantified conditions {x,y,…}∈rdom region or domain specification - ArgMin[{f,cons},x∈rdom] is effectively equivalent to ArgMin[{f,cons∧x∈rdom},x].
- For x∈rdom, the different coordinates can be referred to using Indexed[x,i].
- Possible domains rdom include:
-
Reals real scalar variable Integers integer scalar variable Vectors[n,dom] vector variable in 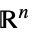
Matrices[{m,n},dom] matrix variable in 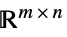
ℛ vector variable restricted to the geometric region 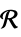
- By default, all variables are assumed to be real.
- ArgMin will return exact results if given exact input. With approximate input, it automatically calls NArgMin.
- If the minimum is achieved only infinitesimally outside the region defined by the constraints, or only asymptotically, ArgMin will return the closest specifiable point.
- Even if the same maximum is achieved at several points, only one is returned.
- If the constraints cannot be satisfied, ArgMin returns {Indeterminate,Indeterminate,…}.
- N[ArgMin[…]] calls NArgMin for optimization problems that cannot be solved symbolically.
Examples
open allclose allBasic Examples (5)
Scope (36)
Basic Uses (7)
Univariate Problems (7)
Multivariate Problems (9)
Multivariate linear constrained minimization:
Linear-fractional constrained minimization:
Unconstrained polynomial minimization:
Constrained polynomial optimization can always be solved:
The minimum value may not be attained:
The objective function may be unbounded:
There may be no points satisfying the constraints:
Quantified polynomial constraints:
Bounded transcendental minimization:
Minimize convex objective function ![]() such that
such that ![]() is positive semidefinite and
is positive semidefinite and ![]() :
:
Parametric Problems (4)
Optimization over Integers (3)
Optimization over Regions (6)
Find the minimum distance between two regions:
Find the minimum ![]() such that the triangle and ellipse still intersect:
such that the triangle and ellipse still intersect:
Find the disk of minimum radius that contains the given three points:
Using Circumsphere gives the same result directly:
Use ![]() to specify that
to specify that ![]() is a vector in
is a vector in ![]() :
:
Options (1)
WorkingPrecision (1)
Finding an exact minimum point can take a long time:
With WorkingPrecision->100, you get an approximate minimum point:
Applications (10)
Basic Applications (3)
Find the lengths of sides of a unit area rectangle with minimal perimeter:
Find the lengths of sides of a unit area triangle with minimal perimeter:
The minimal perimeter triangle is equilateral:
Find a point on a parabola closest to its axis:
Assuming a particular relationship between the ![]() and
and ![]() parameters:
parameters:
Geometric Distances (6)
The point q in a region ℛ that is nearest to a given point p is given by ArgMin[Norm[p-q],q∈ℛ]. Find the nearest point in Disk[] to {1,1}:
Find the nearest point to {1,2} in the standard unit simplex Simplex[2]:
Find the nearest point to {1,1,1} in the standard unit sphere Sphere[]:
Find the nearest point to {-1,1,1} in the standard unit simplex Simplex[3]:
The the nearest points p∈ and q∈ can be found through ArgMin[Norm[p-q],{p∈,q∈}]. Find the nearest points in Disk[{0,0}] and Rectangle[{3,3}]:
Find the nearest points in Line[{{0,0,0},{1,1,1}}] and Ball[{5,5,0},1]:
Geometric Centers (1)
If ℛ⊆n is a region that is full dimensional, then the Chebyshev center is the point p∈ℛ that minimizes SignedRegionDistance[ℛ,p], i.e. the negation of the distance to the complement region. Find the Chebyshev center for Disk[]:
Find the Chebyshev center for Rectangle[]:
Properties & Relations (6)
Minimize gives both the value of the minimum and the minimizer point:
ArgMin gives an exact global minimizer point:
NArgMin attempts to find a global minimizer point numerically, but may find a local minimizer:
FindArgMin finds a local minimizer point depending on the starting point:
The minimum point satisfies the constraints, unless messages say otherwise:
The given point minimizes the distance from the point {2,![]() }:
}:
When the minimum is not attained, ArgMin may give a point on the boundary:
Here the objective function tends to the minimum value when y tends to infinity:
ArgMin can solve linear optimization problems:
LinearOptimization can be used to solve the same problem:
Use RegionNearest to compute a nearest point in the given region:
It can be computed using ArgMin:
Possible Issues (2)
A finite minimum value may not be attained:
The objective function may be unbounded:
There may be no points satisfying the constraints:
ArgMin requires that all functions present in the input be real valued:
Values for which the equation is satisfied but the square roots are not real are disallowed:
Text
Wolfram Research (2008), ArgMin, Wolfram Language function, https://reference.wolfram.com/language/ref/ArgMin.html (updated 2021).
CMS
Wolfram Language. 2008. "ArgMin." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/ArgMin.html.
APA
Wolfram Language. (2008). ArgMin. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ArgMin.html