BiweightMidvariance
BiweightMidvariance[list]
list 中の要素のバイウェイト中間分散の値を与える.
BiweightMidvariance[list,c]
尺度母数 c のバイウェイト中間分散の値を与える.
詳細

- BiweightMidvarianceはロバストな分散推定器である.
- BiweightMidvarianceは,Medianを中心とする重み付きの2次中心モーメントで与えられる.要素が中心から遠ざかるほど,その重みは小さくなる.
- 重み関数の幅尺度は母数 c で制御される.大きい c は統計の計算によりたくさんのデータ値が含まれることを意味し,逆もまた真である.
- リスト{x1,x2,…,xn}については,バイウェイト中間分散推定器の値は
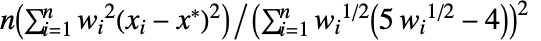 で与えられる.ただし,
で与えられる.ただし,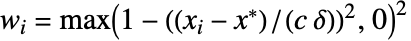 であり,
であり,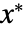 はMedian[{x1,…,xn}],
はMedian[{x1,…,xn}],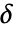 はMedianDeviation[{x1,…,xn}]である.
はMedianDeviation[{x1,…,xn}]である. - BiweightMidvariance[list]はBiweightMidvariance[list,9]に等しい.
- BiweightMidvariance[{{x1,y1,…},{x2,y2,…},…}]は{BiweightMidvariance[{x1,x2,…}],BiweightMidvariance[{y1,y2,…}],…}を与える.
- BiweightMidvarianceでは,c は任意の正の実数でよい.
例題
すべて開くすべて閉じる例 (4)
リストのBiweightMidvariance:
行列の列のBiweightMidvariance:
尺度因数が8であるリストのBiweightMidvariance:
日付のリストのBiweightMidvariance:
スコープ (9)
TimeSeriesのバイウェイト中間分散を求める:
アプリケーション (5)
特性と関係 (3)
区間![]() 外の値は統計に影響しない.ここで,
外の値は統計に影響しない.ここで,![]() はサンプルの中央値,
はサンプルの中央値,![]() は中央値の絶対偏差,
は中央値の絶対偏差,![]() はデフォルト値が9に等しい尺度母数である:
はデフォルト値が9に等しい尺度母数である:
バイウェイト中間分散の計算に使用される重み関数 w(x)の形:
サンプルの最小値と最大値を2倍して,再度バイウェイト中間分散を計算する:
BiweightMidvarianceとVarianceは,データの分散推定器である:
データのサンプルを再度取ってブートストラップ推定を生成する:
各推定器についてブートストラップ推定の標準偏差と平均の比を計算する.より小さい値はより正確な分散測度を意味する:
BiweightMidvarianceは,母数 c の大きい値については2次中心モーメントに収束する:
テキスト
Wolfram Research (2017), BiweightMidvariance, Wolfram言語関数, https://reference.wolfram.com/language/ref/BiweightMidvariance.html (2024年に更新).
CMS
Wolfram Language. 2017. "BiweightMidvariance." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/BiweightMidvariance.html.
APA
Wolfram Language. (2017). BiweightMidvariance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BiweightMidvariance.html