BiweightMidvariance
BiweightMidvariance[list]
给出 list 中元素的双加权中值方差 (biweight midvariance) 的值.
BiweightMidvariance[list,c]
给出缩放参数为 c 的双加权中值方差.
更多信息

- BiweightMidvariance 是稳健分散度估计量
- BiweightMidvariance 由加权二阶中心矩给出,Median 为其中心. 离中心较远的元素的权重也较低.
- 加权函数的宽度由参数 c 控制. 较大的 c 表明在计算统计量时有更多的数据被包含进来,反之亦然.
- 对于列表 {x1,x2,…,xn},双加权中值方差估计器是由
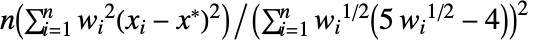 给出,其中
给出,其中 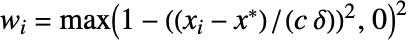 ,
,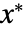 是 Median[{x1,x2,…,xn}],并且
是 Median[{x1,x2,…,xn}],并且 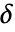 是 MedianDeviation[{x1,x2,…,xn}].
是 MedianDeviation[{x1,x2,…,xn}]. - BiweightMidvariance[list] 等价于 BiweightMidvariance[list,9].
- BiweightMidvariance[{{x1,y1,…},{x2,y2,…},…}] 给出 {BiweightMidvariance[{x1,x2,…}],BiweightMidvariance[{y1,y2,…}],…}.
- BiweightMidvariance 允许 c 为任意正实数.
范例
打开所有单元关闭所有单元基本范例 (4)
列表的 BiweightMidvariance:
矩阵的列的 BiweightMidvariance:
缩放因子为 8 时列表的 BiweightMidvariance:
日期列表的 BiweightMidvariance:
范围 (9)
求 TimeSeries 的双加权中值方差:
应用 (5)
属性和关系 (3)
区间 ![]() 之外的值对统计量没有影响. 这里
之外的值对统计量没有影响. 这里 ![]() 是样本中位数,
是样本中位数,![]() 是绝对中位差.
是绝对中位差. ![]() 是缩放参数,默认值为 9:
是缩放参数,默认值为 9:
BiweightMidvariance 和 Variance 是数据的分散度估计量:
计算每个估计量的自助估计的标准偏差/均值所得的比值;较小的数值表示更准确的分散度量:
当 c 取较大值时,BiweightMidvariance 收敛于第二中心矩:
文本
Wolfram Research (2017),BiweightMidvariance,Wolfram 语言函数,https://reference.wolfram.com/language/ref/BiweightMidvariance.html (更新于 2024 年).
CMS
Wolfram 语言. 2017. "BiweightMidvariance." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/BiweightMidvariance.html.
APA
Wolfram 语言. (2017). BiweightMidvariance. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/BiweightMidvariance.html 年