WOLFRAM

Wolfram 语言与系统 参考资料中心
Wolfram 语言首页 »

BooleanCountingFunction
✖
BooleanCountingFunction

✖

表示 n 元布尔函数，当不超过 kmax 个变量为 True 时，结果为 True.

✖

表示 n 元布尔函数，当恰好有 k 个变量为 True 时，结果为 True.

✖
BooleanCountingFunction[{kmin,kmax},n]

表示一个函数，当 kmin 到 kmax 范围内的变量为 True 时，结果为 True.

✖
BooleanCountingFunction[{{k1,k2,…}},n]

表示一个函数，当 ki 变量为 True 时，结果为 True.

✖
BooleanCountingFunction[spec,{a1,a2,…}]

给出变量 ai 的布尔表达式，相应 spec 指定的布尔统计函数.

✖
BooleanCountingFunction[spec,{a1,a2,…},form]

给出由 form 指定形式的布尔表达式.

更多信息

范例

打开所有单元关闭所有单元

基本范例  (1)常见实例总结

不超过两个条件为真：

In[1]:=1
✖
https://wolfram.com/xid/0tqle3yb8m54ya-dmbny
Out[1]=1

转换为析取范式：

In[2]:=2
✖
https://wolfram.com/xid/0tqle3yb8m54ya-crsc11
Out[2]=2

范围  (6)标准用法实例范围调查

当最多 2 个变量为真时，f 为真：

In[1]:=1
✖
https://wolfram.com/xid/0tqle3yb8m54ya-jahxll
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0tqle3yb8m54ya-cned8o
Out[2]=2

恰好有 2 个变量为真：

In[3]:=3
✖
https://wolfram.com/xid/0tqle3yb8m54ya-i0r30v
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0tqle3yb8m54ya-ihro3s
Out[4]=4

有 2 到 3 个变量为真：

In[5]:=5
✖
https://wolfram.com/xid/0tqle3yb8m54ya-bl3pgk
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0tqle3yb8m54ya-e6ss
Out[6]=6

1、3 或 5 个变量为真：

In[7]:=7
✖
https://wolfram.com/xid/0tqle3yb8m54ya-jzvgdc
Out[7]=7
In[8]:=8
✖
https://wolfram.com/xid/0tqle3yb8m54ya-epiiq5
Out[8]=8

指定当正好有 1、4 或 5 个变量为真时， f 为真：

In[1]:=1
✖
https://wolfram.com/xid/0tqle3yb8m54ya-b0u073
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0tqle3yb8m54ya-cf24sd
Out[2]=2

BooleanCountingFunction 缺省下保留函数形式：

In[1]:=1
✖
https://wolfram.com/xid/0tqle3yb8m54ya-2e8xg
Out[1]=1

用 BooleanConvert 转换到其它形式：

In[2]:=2
✖
https://wolfram.com/xid/0tqle3yb8m54ya-dkn988
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0tqle3yb8m54ya-bn11gc
Out[3]=3

当给出明确的变量列表，BooleanCountingFunction 自动转换：

In[1]:=1
✖
https://wolfram.com/xid/0tqle3yb8m54ya-ejkjco
Out[1]=1

当变量数目增多时，展开的形式会很大：

In[2]:=2
✖
https://wolfram.com/xid/0tqle3yb8m54ya-b27wio
Out[2]=2

对函数形式的计算，性能的改善可能是巨大的：

In[1]:=1
✖
https://wolfram.com/xid/0tqle3yb8m54ya-fjzd0o
In[2]:=2
✖
https://wolfram.com/xid/0tqle3yb8m54ya-fs4nab
In[3]:=3
✖
https://wolfram.com/xid/0tqle3yb8m54ya-b8bbm9
In[4]:=4
✖
https://wolfram.com/xid/0tqle3yb8m54ya-f80wda
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0tqle3yb8m54ya-lz42bz
Out[5]=5

化简常数参数：

In[1]:=1
✖
https://wolfram.com/xid/0tqle3yb8m54ya-mo6wp0
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0tqle3yb8m54ya-bie7ev
Out[2]=2

极端情况自动转换为公式：

In[3]:=3
✖
https://wolfram.com/xid/0tqle3yb8m54ya-cuk5ig
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0tqle3yb8m54ya-nvq12z
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0tqle3yb8m54ya-vu18f
Out[5]=5

应用  (4)用该函数可以解决的问题范例

分别创建不超过、至少或恰好有 k 个变量为真的新指令：

In[1]:=1
✖
https://wolfram.com/xid/0tqle3yb8m54ya-gnlgrn
In[2]:=2
✖
https://wolfram.com/xid/0tqle3yb8m54ya-u9w97
In[3]:=3
✖
https://wolfram.com/xid/0tqle3yb8m54ya-i4i779

沿着单位圆，创建一定数目的扇形区域：

In[4]:=4
✖
https://wolfram.com/xid/0tqle3yb8m54ya-euib0u
Out[4]=4

显示新的组合区域：

In[5]:=5
✖
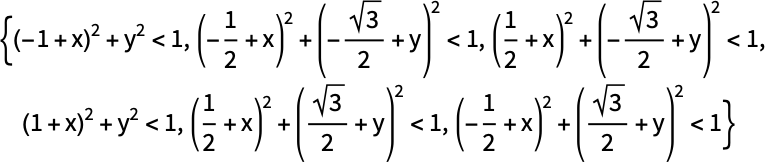
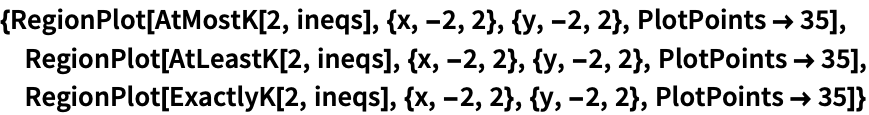
https://wolfram.com/xid/0tqle3yb8m54ya-f67h3j
Out[5]=5

在这些区域上积分：

In[6]:=6
✖
https://wolfram.com/xid/0tqle3yb8m54ya-bfs2st
Out[6]=6
In[7]:=7
✖
https://wolfram.com/xid/0tqle3yb8m54ya-ebxzrw
Out[7]=7

定义一个布尔函数，当真值变量的数目等于 k 模 m 时，函数为真：

In[1]:=1
✖
https://wolfram.com/xid/0tqle3yb8m54ya-k8e0ul

当 k=0 且 m=2 时，则得到 Xnor：

In[2]:=2
✖
https://wolfram.com/xid/0tqle3yb8m54ya-dzd0k3
Out[2]=2

当 k=1 且 m=2 时，则得到 Xor：

In[3]:=3
✖
https://wolfram.com/xid/0tqle3yb8m54ya-gao3o0
Out[3]=3

对其它 k 和 m 值，我们得到新的功能：

In[4]:=4
✖
https://wolfram.com/xid/0tqle3yb8m54ya-e7rznf
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0tqle3yb8m54ya-ff5pf5
Out[5]=5

二维真值表：

In[6]:=6
✖
https://wolfram.com/xid/0tqle3yb8m54ya-dk5vss
Out[6]=6

定义一个布尔真值表，对真值排序：

In[1]:=1
✖
https://wolfram.com/xid/0tqle3yb8m54ya-i8bnt

最后的列表通常是排序：

In[2]:=2
✖
https://wolfram.com/xid/0tqle3yb8m54ya-jffmd2
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0tqle3yb8m54ya-b6fozv
Out[3]=3

求系统的平均无故障时间，该系统由三个组件组成，要求其中两个组件正常工作：

In[1]:=1
✖
https://wolfram.com/xid/0tqle3yb8m54ya-c42t61
In[2]:=2
✖
https://wolfram.com/xid/0tqle3yb8m54ya-hk7kx
In[3]:=3
✖
https://wolfram.com/xid/0tqle3yb8m54ya-dkkjpx
Out[3]=3

属性和关系  (6)函数的属性及与其他函数的关联

BooleanCountingFunction 按它的参数是对称的：

In[1]:=1
✖
https://wolfram.com/xid/0tqle3yb8m54ya-h2ycoq
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0tqle3yb8m54ya-gm06jw
Out[2]=2

BooleanCountingFunction 的逻辑组合相应于在指数上集合操作：

In[1]:=1
✖
https://wolfram.com/xid/0tqle3yb8m54ya-bp412r
In[2]:=2
✖
https://wolfram.com/xid/0tqle3yb8m54ya-k6hgq4
In[3]:=3
✖
https://wolfram.com/xid/0tqle3yb8m54ya-q552hg
Out[3]=3

基本规定可以等价于用 Range 指定：

In[1]:=1
✖
https://wolfram.com/xid/0tqle3yb8m54ya-br2ddu
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0tqle3yb8m54ya-egh492
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0tqle3yb8m54ya-7z83f
Out[3]=3

许多指令可以用 BooleanCountingFunction 的形式指定：

In[1]:=1
✖
https://wolfram.com/xid/0tqle3yb8m54ya-ls69v

And：

In[2]:=2
✖
https://wolfram.com/xid/0tqle3yb8m54ya-bds5ax
In[3]:=3
✖
https://wolfram.com/xid/0tqle3yb8m54ya-fas5ju
Out[3]=3

Or：

In[4]:=4
✖
https://wolfram.com/xid/0tqle3yb8m54ya-gsmhqw
In[5]:=5
✖
https://wolfram.com/xid/0tqle3yb8m54ya-k45jm
Out[5]=5

Nand：

In[6]:=6
✖
https://wolfram.com/xid/0tqle3yb8m54ya-hcois
In[7]:=7
✖
https://wolfram.com/xid/0tqle3yb8m54ya-g18qck
Out[7]=7

Nor：

In[8]:=8
✖
https://wolfram.com/xid/0tqle3yb8m54ya-fxv720
In[9]:=9
✖
https://wolfram.com/xid/0tqle3yb8m54ya-h7j9y
Out[9]=9

Xor：

In[10]:=10
✖
https://wolfram.com/xid/0tqle3yb8m54ya-jjq35g
In[11]:=11
✖
https://wolfram.com/xid/0tqle3yb8m54ya-r2zp
Out[11]=11

Xnor：

In[12]:=12
✖
https://wolfram.com/xid/0tqle3yb8m54ya-ew8qcf
In[13]:=13
✖
https://wolfram.com/xid/0tqle3yb8m54ya-buefqp
Out[13]=13

Equivalent：

In[14]:=14
✖
https://wolfram.com/xid/0tqle3yb8m54ya-c8xadt
In[15]:=15
✖
https://wolfram.com/xid/0tqle3yb8m54ya-fiw5x
Out[15]=15

Majority：

In[16]:=16
✖
https://wolfram.com/xid/0tqle3yb8m54ya-irqnwk
In[17]:=17
✖
https://wolfram.com/xid/0tqle3yb8m54ya-ccslh
Out[17]=17

BooleanCountingFunction 的真值集的大小是 Subsets 的长度：

In[1]:=1
✖
https://wolfram.com/xid/0tqle3yb8m54ya-d6h3kx
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0tqle3yb8m54ya-hm4qde
Out[2]=2

BooleanCountingFunction 的真值集的大小可以由组合和给出：

In[1]:=1
✖
https://wolfram.com/xid/0tqle3yb8m54ya-2b3nj
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0tqle3yb8m54ya-gh069s
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0tqle3yb8m54ya-g7h9j
Out[3]=3

巧妙范例  (1)奇妙或有趣的实例

当恰好 i 个变量为真时，BooleanCountingFunction 具有不相交的真值集：

In[1]:=1
✖
https://wolfram.com/xid/0tqle3yb8m54ya-bx1d5t
Out[1]=1
In[2]:=2
✖
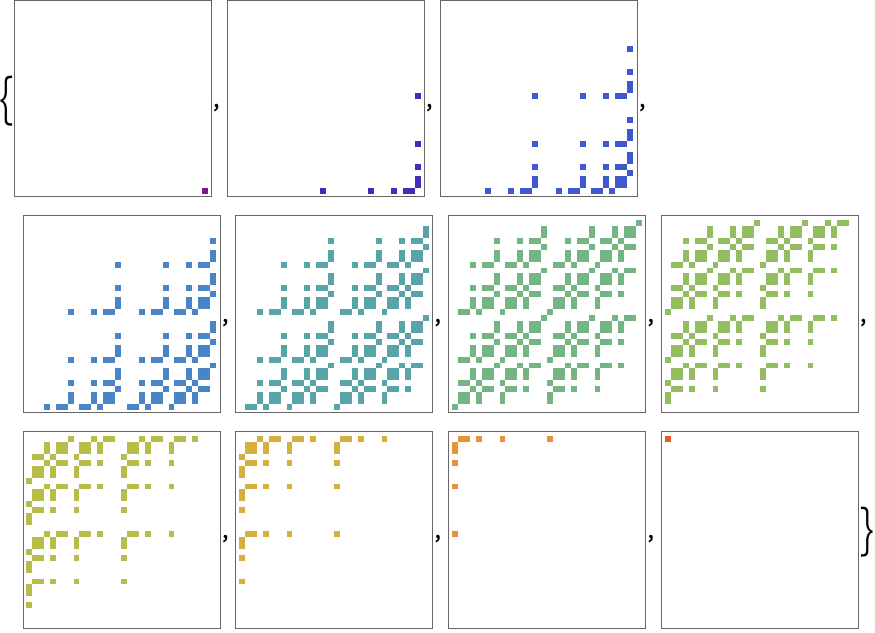
https://wolfram.com/xid/0tqle3yb8m54ya-h2r9w
Out[2]=2
Wolfram Research (2008)，BooleanCountingFunction，Wolfram 语言函数，https://reference.wolfram.com/language/ref/BooleanCountingFunction.html.
✖
Wolfram Research (2008)，BooleanCountingFunction，Wolfram 语言函数，https://reference.wolfram.com/language/ref/BooleanCountingFunction.html.

文本

Wolfram Research (2008)，BooleanCountingFunction，Wolfram 语言函数，https://reference.wolfram.com/language/ref/BooleanCountingFunction.html.

✖
Wolfram Research (2008)，BooleanCountingFunction，Wolfram 语言函数，https://reference.wolfram.com/language/ref/BooleanCountingFunction.html.

CMS

Wolfram 语言. 2008. "BooleanCountingFunction." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/BooleanCountingFunction.html.

✖
Wolfram 语言. 2008. "BooleanCountingFunction." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/BooleanCountingFunction.html.

APA

Wolfram 语言. (2008). BooleanCountingFunction. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/BooleanCountingFunction.html 年

✖
Wolfram 语言. (2008). BooleanCountingFunction. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/BooleanCountingFunction.html 年

BibTeX

@misc{reference.wolfram_2025_booleancountingfunction, author="Wolfram Research", title="{BooleanCountingFunction}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/BooleanCountingFunction.html}", note=[Accessed: 04-April-2025 ]}

✖
@misc{reference.wolfram_2025_booleancountingfunction, author="Wolfram Research", title="{BooleanCountingFunction}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/BooleanCountingFunction.html}", note=[Accessed: 04-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_booleancountingfunction, organization={Wolfram Research}, title={BooleanCountingFunction}, year={2008}, url={https://reference.wolfram.com/language/ref/BooleanCountingFunction.html}, note=[Accessed: 04-April-2025 ]}

✖
@online{reference.wolfram_2025_booleancountingfunction, organization={Wolfram Research}, title={BooleanCountingFunction}, year={2008}, url={https://reference.wolfram.com/language/ref/BooleanCountingFunction.html}, note=[Accessed: 04-April-2025 ]}