discretizes the region reg into a BoundaryMeshRegion.
BoundaryDiscretizeRegion[reg,{{xmin,xmax},…}]
restricts to the bounds ![]() .
.




BoundaryDiscretizeRegion
discretizes the region reg into a BoundaryMeshRegion.
BoundaryDiscretizeRegion[reg,{{xmin,xmax},…}]
restricts to the bounds ![]() .
.
Details and Options

- BoundaryDiscretizeRegion is also known as boundary evaluation.
- BoundaryDiscretizeRegion effectively discretizes the boundaries of the full-dimensional parts of a region reg.
- The region reg can be anything that is ConstantRegionQ and RegionEmbeddingDimension less or equal to 3.
- BoundaryDiscretizeRegion has the same options as BoundaryMeshRegion, with the following additions and changes:
-
AccuracyGoal Automatic digits of accuracy sought MaxCellMeasure Automatic maximum cell measure Method Automatic method to use PerformanceGoal $PerformanceGoal whether to consider speed or quality PrecisionGoal Automatic digits of precision sought - With AccuracyGoal->a and PrecisionGoal->p, an attempt will be made to keep the maximum distance between the region reg or the discretized region dreg and any point in RegionSymmetricDifference[reg,dreg] to less than
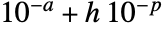 , where
, where  is the length of the diagonal of the bounding box.
is the length of the diagonal of the bounding box. - With MaxCellMeasure->m where m>0, the cell measure in the boundary dimension d-1 where d is the region dimension will be limited to m. Measure limits for specific dimensions may be specified with MaxCellMeasure->{…,di->mi,…}.

Examples
open all close allBasic Examples (2)
Scope (24)
Regions in 1D (5)
Line and Interval are full-dimensional regions in 1D:
An ImplicitRegion is 1D if it has one variable:
The discretization can be clipped to a specified range:
A ParametricRegion is 1D if it has only one function:
The discretization can be clipped to a specified range:
Because this region is unbounded, clip it to discretize:
A BooleanRegion in 1D:
Boundary discretization can only represent full-dimensional region components:
Use DiscretizeRegion to discretize lower-dimensional components as well:
Regions in 2D (8)
Rectangle, Disk, and Simplex are special regions that can be full dimensional in 2D:
Disk:
An ImplicitRegion is 2D if it has two variables:
For an unbounded region, clip the discretization to a specified range:
A ParametricRegion is in 2D if it has two functions:
A region in 2D with parameters constrained to a unit disk:
Parameters constrained to a rectangle:
Given two exact regions, ParametricRegion can be used to represent their Minkowski sum:
A RegionUnion in 2D:
A region can include components of different dimensions:
The boundary discretization can only represent full-dimensional components, however:
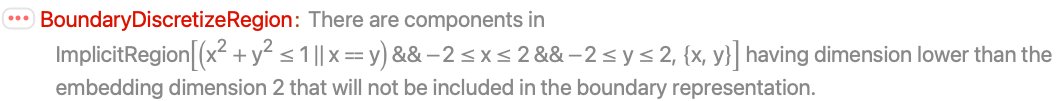
A polygon with GeoGridPosition:
Regions in 3D (5)
Cuboid, Ellipsoid, and Simplex are special regions that can be full dimensional in 3D:
An ImplicitRegion is 3D if it has precisely three variables:
A ParametricRegion is in 3D if it has precisely three functions:
A solid in 3D generated with the parameters constrained to the unit ball:
A region can include components of different dimensions:
The boundary discretization can only represent full-dimensional components, however:

Detail (2)
The measure of cells in the discretization can be controlled using MaxCellMeasure:
By default, when given as a number, it applies to the boundary dimension:
With area a, a length l is computed so that triangles with sides of length l will have area a:
Using TriangulateMesh with the same specification will maintain quality near the edge:
For nonlinear regions, the measure of boundary cells depends on several options:
The length of any segment may be controlled by MaxCellMeasure:
The default PrecisionGoal is chosen to be a value so that curves appear as visually smooth:
MaxCellMeasure->∞ may be used to base the boundary measure on precision:
PrecisionGoal->None may be used to base the boundary measure on MaxCellMeasure:
AccuracyGoal->a may be used to specify an absolute tolerance ![]() :
:
The default is for MaxCellMeasure to apply to the boundary dimension:
The measure on the boundary may be further restricted by approximation requirements:
Quality (4)
The measure of cells in the discretization can be controlled using MaxCellMeasure:
By default, this controls the measure of the edges:
Use AccuracyGoal to ensure the discretized boundary is close to the exact boundary:
The discretization with the higher AccuracyGoal is closer to the true boundary:
Use PrecisionGoal to ensure the discretized boundary is close to the exact boundary:
The discretization with the higher PrecisionGoal is closer to the true boundary:
Set PerformanceGoal to "Quality" for a high-quality discretization:
Or to "Speed" for a faster discretization that may be of lower quality:
Options (24)
AccuracyGoal (1)
MaxCellMeasure (2)
With MaxCellMeasure->m, boundary cell size is less than or equal to ![]() :
:
This gives the lengths of the segments:
In 3D, the area of faces is controlled by MaxCellMeasure:
This gives the areas of the faces:
The lengths of edges can be controlled by setting a max measure for "Length":
MeshCellHighlight (3)
MeshCellHighlight allows you to specify highlighting for parts of a BoundaryMeshRegion:
By making faces transparent, the internal structure of a 3D BoundaryMeshRegion can be seen:
MeshCellLabel (3)
MeshCellLabel can be used to label parts of a BoundaryMeshRegion:
Label the vertices and edges of a rectangle:
MeshCellMarker (1)
MeshCellMarker can be used to assign values to parts of a BoundaryMeshRegion:
Use MeshCellLabel to show the markers:
MeshCellShapeFunction (2)
MeshCellShapeFunction allows you to specify functions for parts of a BoundaryMeshRegion:
MeshCellStyle (3)
MeshCellStyle allows you to specify styling for parts of a BoundaryMeshRegion:
By making faces transparent, the internal structure of a 3D BoundaryMeshRegion can be seen:
Method (6)
The "Continuation" method uses a curve continuation method that can in many cases resolve corners, cusps, and sharp changes quite well:
The "RegionPlot" method is based on improving output from RegionPlot and can sometimes be faster:
The "Boolean" method is optimized for Boolean regions:
The "DiscretizeGraphics" method is optimized for graphics primitives:
The "RegionPlot3D" method for 3D regions is based on RegionPlot3D:
The "ContourPlot3D" method for 3D regions is based on ContourPlot3D:
Applications (2)
Properties & Relations (5)
The output of BoundaryDiscretizeRegion is a BoundaryMeshRegion:
Given a boundary discretization, TriangulateMesh can discretize the interior:
The boundary discretization represents the regular closure of a region:
The lower-dimensional component is lost, but can be represented by DiscretizeRegion:
BoundaryDiscretizeRegion can discretize a region with holes:
BoundaryDiscretizeRegion can discretize a region with disjoint components:
Related Guides
Text
Wolfram Research (2014), BoundaryDiscretizeRegion, Wolfram Language function, https://reference.wolfram.com/language/ref/BoundaryDiscretizeRegion.html (updated 2015).
CMS
Wolfram Language. 2014. "BoundaryDiscretizeRegion." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/BoundaryDiscretizeRegion.html.
APA
Wolfram Language. (2014). BoundaryDiscretizeRegion. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BoundaryDiscretizeRegion.html
BibTeX
@misc{reference.wolfram_2025_boundarydiscretizeregion, author="Wolfram Research", title="{BoundaryDiscretizeRegion}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/BoundaryDiscretizeRegion.html}", note=[Accessed: 06-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_boundarydiscretizeregion, organization={Wolfram Research}, title={BoundaryDiscretizeRegion}, year={2015}, url={https://reference.wolfram.com/language/ref/BoundaryDiscretizeRegion.html}, note=[Accessed: 06-December-2025]}