将区域 reg 离散化为 BoundaryMeshRegion.
BoundaryDiscretizeRegion[reg,{{xmin,xmax},…}]
限制范围为 ![]() .
.




BoundaryDiscretizeRegion
将区域 reg 离散化为 BoundaryMeshRegion.
BoundaryDiscretizeRegion[reg,{{xmin,xmax},…}]
限制范围为 ![]() .
.
更多信息和选项

- BoundaryDiscretizeRegion 也被称作边界计算.
- BoundaryDiscretizeRegion 对区域 reg 全方位部分的边界进行有效地离散.
- 区域 reg 可以是任意满足 ConstantRegionQ 和小于或等于 3 的 RegionEmbeddingDimension.
- BoundaryDiscretizeRegion 具有与 BoundaryMeshRegion 相同的选项,并有以下增加和改变:
-
AccuracyGoal Automatic 所追求的准确度位数 MaxCellMeasure Automatic 最大单元度量 Method Automatic 所用方法 PerformanceGoal $PerformanceGoal 考虑速度还是质量 PrecisionGoal Automatic 所追求的精度位数 - 在设置 AccuracyGoal->a 和 PrecisionGoal->p 下,将尝试把区域 reg 或离散化区域 dreg 与 RegionSymmetricDifference[reg,dreg] 中任意点之间的距离保持在
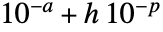 以内,其中
以内,其中 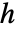 为边界框对角线的长度.
为边界框对角线的长度. - 当 MaxCellMeasure->m 时,其中 m>0,边界维数为 d-1 的单元度量将被限定为 m,其中 d 是区域维数. 具体维数的度量极限可以通过 MaxCellMeasure->{…,di->mi,…} 指定.

范例
打开所有单元 关闭所有单元范围 (24)
一维区域 (5)
如果 ImplicitRegion 有一个变量,则它是一维的:
如果 ParametricRegion 仅有一个函数,则它是一维的:
一维中的 BooleanRegion:
也可以使用 DiscretizeRegion 离散化低维分量:
二维区域 (8)
Rectangle、Disk 和 Simplex 是在二维中可以是全维的特殊区域:
Disk:
如果 ImplicitRegion 有两个变量,则它是二维的:
如果 ParametricRegion 有两个函数,则是二维的:
已知两个精确区域,ParametricRegion 可以用来表示它们的的闵可夫斯基和:
二维中的 RegionUnion:
具有 GeoGridPosition 的多边形:
三维区域 (5)
Cuboid、Ellipsoid 和 Simplex 是在三维中可以是全维的特殊区域:
如果 ImplicitRegion 有精确的三个变量,则它是三维的:
如果 ParametricRegion 恰好有三个函数,则是三维的:

详细信息 (2)
使用 MaxCellMeasure 可以控制离散化中的单元测量:
由于面积为 a,长度 l 可以通过面积为 a、边长为 l 的三角形计算得到:
使用相同规范的 TriangulateMesh 将使质量保持在边缘附近:
任何线段的长度可以通过 MaxCellMeasure 控制:
默认 PrecisionGoal 所选的值使得曲线视觉上显得平滑:
MaxCellMeasure->∞ 可用于将边界度量基于精度:
PrecisionGoal->None 可用于将边界度量基于 MaxCellMeasure:
AccuracyGoal->a 可用于指定绝对绝对公差 ![]() :
:
默认情况下,MaxCellMeasure 应用边界维度:
质量 (4)
离散化中的单元度量可以使用 MaxCellMeasure 控制:
使用 AccuracyGoal 来确保离散后的边界接近确切边界:
具有较高 AccuracyGoal 的离散化距离真实边界较近:
使用 PrecisionGoal 来确保离散后的边界接近确切边界:
具有较高 PrecisionGoal 的离散化距离真实边界较近:
设定 PerformanceGoal 为 "Quality" 以得到高质量的离散化:
选项 (24)
MaxCellMeasure (2)
在 MaxCellMeasure->m 时,边界单元尺寸小于或等于 ![]() :
:
在三维空间中,各面的面积由 MaxCellMeasure 控制:
MeshCellHighlight (3)
MeshCellHighlight 允许指定部分 BoundaryMeshRegion 的突出显示:
通过使表面透明,可以看见三维 BoundaryMeshRegion 的内部结构:
MeshCellLabel (3)
MeshCellMarker (1)
MeshCellMarker 可用于给部分 BoundaryMeshRegion 赋值:
使用 MeshCellLabel 显示标记:
MeshCellShapeFunction (2)
MeshCellStyle (3)
MeshCellStyle 允许指定部分 BoundaryMeshRegion 的样式:
通过使表面透明,可以看见三维 BoundaryMeshRegion 的内部结构:
Method (6)
方法 "Continuation" 使用曲线延拓方法,在许多情况下可以处理角、尖和急剧变化的情况:
方法 "RegionPlot" 基于改善 RegionPlot 的输出,有些时候使得速度较快:
方法 "DiscretizeGraphics" 对于图形基元是最优化的:
用于三维区域的方法 "RegionPlot3D" 基于 RegionPlot3D:
用于三维区域的方法 "ContourPlot3D" 基于 ContourPlot3D:
应用 (2)
属性和关系 (5)
BoundaryDiscretizeRegion 的输出是 BoundaryMeshRegion:
已知边界离散,TriangulateMesh 能够离散内部:
较低维的分量丢失,但可以通过 DiscretizeRegion 表示:
BoundaryDiscretizeRegion 可以离散有孔的区域:
BoundaryDiscretizeRegion 可对具有不相交部分的区域进行离散化:
文本
Wolfram Research (2014),BoundaryDiscretizeRegion,Wolfram 语言函数,https://reference.wolfram.com/language/ref/BoundaryDiscretizeRegion.html (更新于 2015 年).
CMS
Wolfram 语言. 2014. "BoundaryDiscretizeRegion." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/BoundaryDiscretizeRegion.html.
APA
Wolfram 语言. (2014). BoundaryDiscretizeRegion. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/BoundaryDiscretizeRegion.html 年
BibTeX
@misc{reference.wolfram_2025_boundarydiscretizeregion, author="Wolfram Research", title="{BoundaryDiscretizeRegion}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/BoundaryDiscretizeRegion.html}", note=[Accessed: 19-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_boundarydiscretizeregion, organization={Wolfram Research}, title={BoundaryDiscretizeRegion}, year={2015}, url={https://reference.wolfram.com/language/ref/BoundaryDiscretizeRegion.html}, note=[Accessed: 19-February-2026]}