BrownianBridgeProcess
BrownianBridgeProcess[σ,{t1,a},{t2,b}]
時点 t1における値 a から時点 t2における値 b までの,ボラティリティ σ のブラウン(Brownian)橋過程を表す.
BrownianBridgeProcess[{t1,a},{t2,b}]
時点 t1における値 a から時点 t2における値 b までの標準ブラウン橋過程を表す.
BrownianBridgeProcess[t1,t2]
時点 t1と t2において0でピン止めされた標準ブラウン橋過程を表す.
時点0と1において0でピン止めされた標準ブラウン橋過程を表す.
詳細
- BrownianBridgeProcessはピン止めブラウン運動過程としても知られている.
- BrownianBridgeProcessは連続時間・連続状態のランダム過程である.
- ブラウン橋過程の状態
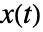 は,
は,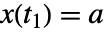 と
と 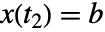 を満足する.
を満足する. - 状態
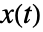 は,NormalDistribution[a+(b-a) (t-t1)/(t2-t1),
は,NormalDistribution[a+(b-a) (t-t1)/(t2-t1),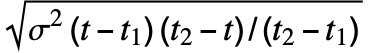 ]に従う.
]に従う. - 母数 σ,t1,t2,a,b は,σ が正で,t2が t1より大きくなるような,任意の実数でよい.
- BrownianBridgeProcessは,Mean,PDF,Probability,RandomFunction等の関数で使うことができる.
例題
すべて開くすべて閉じるスコープ (13)
基本的な用法 (8)
過程スライス特性 (5)
特性と関係 (9)
ブラウン橋過程は特別なItoProcessである:
StratonovichProcessでもある:
ブラウン橋過程は,始めのうちは,対応するWienerProcessに従う:
BrownianBridgeProcessの絶対上限の分布は,Kolmogorov分布に従う:
累積ヒストグラムをKolmogorov分布の累積分布関数と比較する:
BrownianBridgeProcessは,WienerProcessから直接シミュレーションすることができる:
対応するBrownianBridgeProcessと比較する:
ブラウン橋過程は条件付きのWienerProcessである:
テキスト
Wolfram Research (2012), BrownianBridgeProcess, Wolfram言語関数, https://reference.wolfram.com/language/ref/BrownianBridgeProcess.html.
CMS
Wolfram Language. 2012. "BrownianBridgeProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BrownianBridgeProcess.html.
APA
Wolfram Language. (2012). BrownianBridgeProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BrownianBridgeProcess.html