Catalan

Catalan

is Catalan's constant, with numerical value .

Details

  • Mathematical constant treated as numeric by NumericQ and as a constant by D.
  • Catalan can be evaluated to any numerical precision using N.
  • Catalan's constant is given by the sum .

Background & Context

  • Catalan is the symbol representing the mathematical constant known as Catalan's constant. Catalan is defined as the infinite alternating sum of reciprocals of squared odd integers 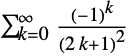and has numerical value 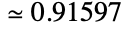. Catalan commonly appears in estimates of combinatorial functions and in certain classes of sums and definite integrals. Catalan also arises in particular values of special functions such as DirichletBeta, Zeta, and PolyLog.
  • When Catalan is used as a symbol, it is propagated as an exact quantity. Expansion and simplification of complicated expressions involving Catalan may require use of functions such as FunctionExpand and FullSimplify.
  • It is not currently known if Catalan is rational (meaning it can be expressed as a ratio of integers), algebraic (meaning it is the root of some integer polynomial), or normal (meaning the digits in its base- expansion are equally distributed) to any base.
  • Catalan can be evaluated to arbitrary numerical precision by means of a rapidly converging Zeilberger-type sum using N. In fact, calculating the first hundred thousand decimal digits of Catalan takes only a fraction of a second on a modern desktop computer. RealDigits can be used to return a list of digits of Catalan and ContinuedFraction to obtain terms of its continued fraction expansion.

Examples

open allclose all

Basic Examples  (1)

Evaluate to high precision:

Scope  (2)

Use in an exact numerical computation:

TraditionalForm formatting:

Applications  (3)

The first 20 digits of Catalan in base 10:

20 digits after the first 1000 digits of Catalan in base 10:

Frequency of coprime Gaussian integers:

Compare with the exact asymptotic result:

Properties & Relations  (2)

Various symbolic relations are automatically used:

Many mathematical functions and operations give results involving Catalan:

Possible Issues  (1)

It is currently not known if Catalan is an algebraic number:

Neat Examples  (3)

Plot a random walk corresponding to the binary digits of Catalan:

Terms in the continued fraction:

Weyl‐type sum involving Catalan:

Wolfram Research (1988), Catalan, Wolfram Language function, https://reference.wolfram.com/language/ref/Catalan.html.

Text

Wolfram Research (1988), Catalan, Wolfram Language function, https://reference.wolfram.com/language/ref/Catalan.html.

CMS

Wolfram Language. 1988. "Catalan." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Catalan.html.

APA

Wolfram Language. (1988). Catalan. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Catalan.html

BibTeX

@misc{reference.wolfram_2024_catalan, author="Wolfram Research", title="{Catalan}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/Catalan.html}", note=[Accessed: 03-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_catalan, organization={Wolfram Research}, title={Catalan}, year={1988}, url={https://reference.wolfram.com/language/ref/Catalan.html}, note=[Accessed: 03-December-2024 ]}