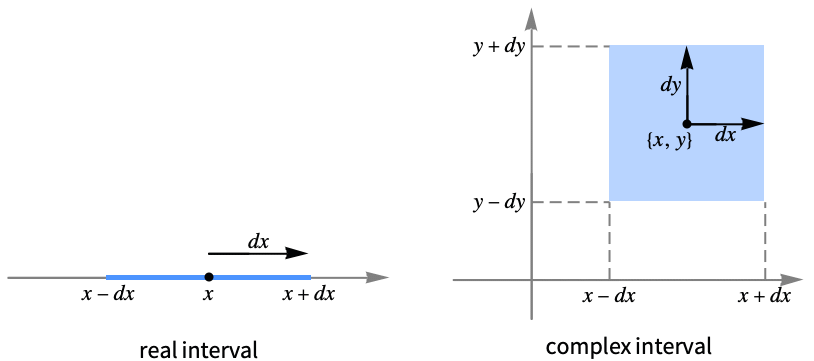
CenteredInterval[x,dx]
对于实数 x 和 dx 给出一个包含实数区间 ![]() 的中心区间.
的中心区间.
CenteredInterval[x+ y,dx+ dy]
给出一个包含复数矩形 ![]() 的中心区间.
的中心区间.
对于近似数 c 给出一个中心区间,该区间包含 c 的误差范围内的所有值.


CenteredInterval
CenteredInterval[x,dx]
对于实数 x 和 dx 给出一个包含实数区间 ![]() 的中心区间.
的中心区间.
CenteredInterval[x+ y,dx+ dy]
给出一个包含复数矩形 ![]() 的中心区间.
的中心区间.
对于近似数 c 给出一个中心区间,该区间包含 c 的误差范围内的所有值.
更多信息


- 中心区间也称为中心半径或中间半径区间.
- CenteredInterval 通常用于获得通过数值计算累积的误差的确信范围. 给定函数所有参数的误差范围,中心区间计算为函数值中的误差提供了可靠的范围.
- CenteredInterval[…] 给出中心为
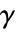 、半径为
、半径为 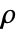 的中心区间对象 Δ,其中
的中心区间对象 Δ,其中 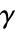 和
和 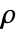 是具有两个分母幂的高斯有理数. 如果
是具有两个分母幂的高斯有理数. 如果 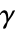 和
和 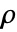 为实数,则 Δ 表示实数区间
为实数,则 Δ 表示实数区间 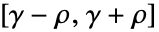 ;否则 Δ 表示复数矩形
;否则 Δ 表示复数矩形 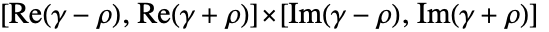 .
. - 算术运算和许多数学函数使用中心区间参数. 对于任何 ai∈Δi,f[Δ1,…,Δn] 生成包含 f[a1,…,an] 的中心区间对象 Δ.
- IntervalMemberQ 可用于确定区间成员或区间之间的包含.
- 只要给定不相交的区间,Equal 和 Less 之类的关系运算符就会产生明确的 True 或 False 结果.
- 在 StandardForm 和相关格式中,CenteredInterval 对象以省略形式打印,仅显示中心和半径的近似值.
- Normal 将 CenteredInterval 对象转换为精度与半径对应的任意精度数.
- Information[CenteredInterval[…], prop] 给出中心半径区间的属性 prop. 可以指定以下属性:
-
"Center" 区间的中心 "Radius" 区间的半径 "Bounds" 区间内值的界限 - 线性代数运算,如 Det、Inverse、LinearSolve 和 Eigensystem,可用于有 CenteredInterval 项的矩阵.
范例
打开所有单元 关闭所有单元基本范例 (3)
范围 (27)
构造中心-半径区间 (7)
将有界 Interval 对象转换为中心区间:
非零机器精度数被视为具有 $MachinePrecision 精确数字的数:
区间算术 (5)
如果值集是无界的,则区间算术运算返回 Indeterminate:
区间属性 (5)
使用 IntervalIntersection 计算交点:
空区间表示为 Interval[]:
线性代数 (10)
CenteredInterval 矩阵的乘积:
将 CenteredInterval 矩阵提升到整数幂:
验证 mpow 包含了 MatrixPower[mrep,17]:
CenteredInterval 矩阵的指数:
CenteredInterval 矩阵的行列式:
CenteredInterval 矩阵的逆矩阵:
求解 CenteredInterval 矩阵中 ![]() :
:
验证 sol 包含 LinearSolve[mrep,brep]:
CenteredInterval 矩阵的特征系统:
验证矢量重新排序和缩放后,vals 包含 rvals,vecs 包含 rvecs:
CenteredInterval 矩阵的 LU 分解:
实对称正定 CenteredInterval 矩阵的 Cholesky 分解:
CenteredInterval 矩阵的特征多项式:
属性和关系 (2)
Interval 表示通过指定端点给出的实际区间:
将区间转换为 CenteredInterval 表示:
可能存在的问题 (1)
文本
Wolfram Research (2021),CenteredInterval,Wolfram 语言函数,https://reference.wolfram.com/language/ref/CenteredInterval.html.
CMS
Wolfram 语言. 2021. "CenteredInterval." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/CenteredInterval.html.
APA
Wolfram 语言. (2021). CenteredInterval. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CenteredInterval.html 年
BibTeX
@misc{reference.wolfram_2025_centeredinterval, author="Wolfram Research", title="{CenteredInterval}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/CenteredInterval.html}", note=[Accessed: 18-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_centeredinterval, organization={Wolfram Research}, title={CenteredInterval}, year={2021}, url={https://reference.wolfram.com/language/ref/CenteredInterval.html}, note=[Accessed: 18-January-2026]}