Circle

Circle[{x,y},r]

半径 r で{x,y}を中心とする円を表す．

Circle[{x,y}]

半径1の円を与える．

Circle[{x,y},{rx,ry}]

半軸の長さが rx と ry の，座標軸と平行である楕円を与える．

Circle[{x,y},…,{θ1,θ2}]

角 θ1と θ2で与えられる円状のもの，つまり楕円の円弧を与える．

詳細

  • パラメータ設定の異なるCircleは，弧，円弧，半円，楕円等としても知られている．
  • Circleは，幾何学領域として，またグラフィックスプリミティブとして使うことができる．
  • Circle[]はCircle[{0,0}]に等しい． »
  • Circleは曲線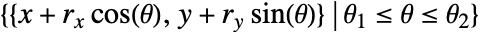を表す．
  • 角は，正の x 方向から反時計回りにラジアン単位で測られる．
  • CircleはGraphicsで使うことができる．
  • グラフィックスでは，点{x,y}と半径 r および{rx,ry}はScaled，Offset，ImageScaled，Dynamicの各式でよい．
  • グラフィックスの描画は，Thickness，Dashing，色等の指示子の影響を受ける．
  • CircleはGeometricSceneの記号的な点や数量と一緒に使うことができる，

予備知識

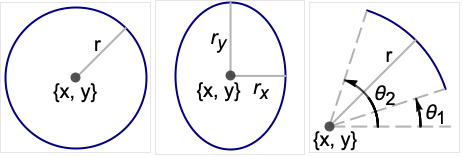
  • Circleは，平面上の円，楕円，あるいは円／楕円の円弧を表すグラフィックスおよび幾何のプリミティブである．Circle[{x,y},r]は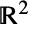における{x,y}を中心とする半径 r の円を，Circle[{x,y},{rx,ry}]は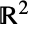における中心が{x,y}で半軸の長さが rxと ryの軸と平行な楕円を，Circle[{x,y},…,{θ1,θ2}]は（楕円である可能性が高い）{x,y}を中心とした正の 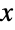軸から時計回りにラジアン単位で測った角度が θ1から θ2までの円弧を表す．略記形式のCircle[{x,y}]はCircle[{x,y},1]に等しく，Circle[] を評価すると自動的にCircle[{0,0},1]になる．
  • CircleオブジェクトはGraphics式の中に置いてフォーマットすることができる．理論的な円の次元は1で太さは0であるが，便宜上，フォーマットされたCircleオブジェクトは，デフォルトで，有限の太さを持って描画される点に注意のこと．グラフィックス内のCircleオブジェクトの外観は，Thickness，AbsoluteThickness，Thick，Thin等の太さの指示子，Dashing，AbsoluteDashing，Dashed，Dotted，DotDashed等の破線指示子，Red等の色指示子，不透明度／透明度の指示子Opacity，スタイルオプションAntialiasingを使って変更することができる．
  • Circleは，計算を行うべき領域指定としても使うことができる．例えば，Integrate[1,{x, y}∈Circle[{0,0},r]]とArcLength[Circle[{x,y},r]]はどちらも円周 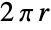を返す．
  • CirclePointsを使って円周上の等間隔に並んだ位置を与えることができる．
  • Circleは他の数多くのシンボルに関係している．CircleはRegionBoundary[Disk[{x,y},r]]を使って計算できるような円板の境界を表す．CylinderおよびSphereは，より高次元における円の相似形と考えることができる．Circle[{x,y},r]は，Sphere[{x,y},r]，ImplicitRegion[(x-u)2+(y-v)2r2,{u,v}]，あるいはParametricRegion[{x+r Cos[t],y+r Sin[t]},{t,0,2π}]を使って表すことができる．PlaneCurveData["entity","property"]あるいはEntityValue[Entity["PlaneCurve","entity"],"property"]を使って標準位置にある円およびその異形の計算済みの特性を得ることができる．"entity"には，"Circle"，"CircularArc"，"Ellipse"，"Semicircle"等の一つを使う．

例題

すべて開くすべて閉じる

例  (5)

単位円：

円弧：

楕円：

さまざまなスタイルの円：

円のArcLength：

長さ，すなわち円弧：

スコープ  (23)

グラフィックス  (13)

指定  (6)

半径を指定する：

中心を指定する：

円弧：

楕円：

楕円弧：

原点における単位円の短縮形：

スタイリング  (3)

太さが異なる円：

スケールされたサイズによる太さ：

印刷用ポイント数による太さ：

破線による円：

彩色された円：

座標  (4)

スケールされた(Scaled)座標と半径を使う：

画像がスケールされた(ImageScaled)座標と半径を使う：

Offset座標を使う：

Offsetを使って半径を印刷用ポイント数で指定する：

領域  (10)

埋込み次元：

幾何次元：

点の帰属判定：

点の帰属条件を求める：

円弧長：

重心：

点からの距離：

単位円についての最近点までの距離：

点からの符号付き距離：

単位円までの符号付き距離：

領域内の最近点：

最近点：

円は有界である：

領域を求める：

円上でIntegrate：

円上で最適化する：

円内で方程式を解く：

アプリケーション  (8)

円の四方充填：

円の六方充填：

楕円歯車のシミュレーション：

LineとCircleの交点を求める：

2つの円の交点を求める：

関数の曲率の半径を示す：

外接円とは，平面上の同一線上にはない3点によって定義される円のことである：

Circumsphereから半径と外心を抽出することができる：

DelaunayMeshを定義する特性は，どの入力点もメッシュ中の任意のTriangleの外接円には含まれないということである：

円状のケーブルに沿って電荷密度を与え，Integrateを使って全電荷を求める：

特性と関係  (10)

Rotateを使って可能なすべての楕円を得る：

Diskを使って塗り潰された円を作成する：

円の3Dにおける一般化はSphereである：

円の陰的な指定はContourPlotで生成できる：

円のパラメータ的な指定はParametricPlotで生成できる：

Sphereは任意のCircleを表すことができる：

Circumsphereは任意のCircleを表すことができる：

ParametricRegionは任意のCircleを表すことができる：

ImplicitRegionは任意のCircleを表すことができる：

Circleはユークリッドノルムのノルム円である：

考えられる問題  (2)

スケールされた(Scaled)半径の使用はPlotRangeに依存する：

ImageScaledのサイズの使用はImageSizeとAspectRatioに依存する：

おもしろい例題  (4)

ランダムな円：

生命の種：

一群の円：

陰陽：

Wolfram Research (1991), Circle, Wolfram言語関数， https://reference.wolfram.com/language/ref/Circle.html （2014年に更新）.

テキスト

Wolfram Research (1991), Circle, Wolfram言語関数， https://reference.wolfram.com/language/ref/Circle.html （2014年に更新）.

CMS

Wolfram Language. 1991. "Circle." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/Circle.html.

APA

Wolfram Language. (1991). Circle. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Circle.html

BibTeX

@misc{reference.wolfram_2024_circle, author="Wolfram Research", title="{Circle}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Circle.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_circle, organization={Wolfram Research}, title={Circle}, year={2014}, url={https://reference.wolfram.com/language/ref/Circle.html}, note=[Accessed: 21-November-2024 ]}