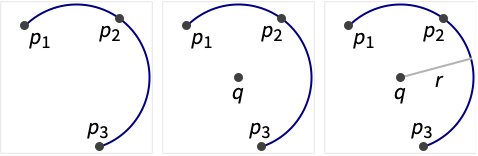
CircularArcThrough

CircularArcThrough[{p1,p2,…}]

represents a circular arc passing through the points pi.

CircularArcThrough[{p1,p2,…},q]

represents a circular arc with center q.

CircularArcThrough[{p1,p2,…},q,r]

represents a circular arc with radius r.

Details

Examples

open allclose all

Basic Examples  (2)

A circular arc passing through three points:

Display the arc:

ArcLength of an arc passing through a set of points:

Scope  (3)

CircularArcThrough works on coordinates:

Multiple points:

Specify constraints for the center of the circular arc:

Constraints on the radius:

CircularArcThrough works with points in 2D:

Applications  (3)

Basic Applications  (3)

Visualize the arc passing through three points:

Find the implicit representation of the arc passing through three points:

The parametric representation:

Find the circumcircle of a triangle:

Properties & Relations  (5)

CircularArcThrough returns a Circle:

Use RegionMember to test point membership:

CircularArcThrough gives a circular arc passing through points:

Obtain the full circle:

Use RegionFit to find a circle that fits a set of points:

The arc passing the first 3 points:

Use CirclePoints to generate equally spaced points on the unit circle:

An arc passing through points on the unit circle:

Wolfram Research (2022), CircularArcThrough, Wolfram Language function, https://reference.wolfram.com/language/ref/CircularArcThrough.html.

Text

Wolfram Research (2022), CircularArcThrough, Wolfram Language function, https://reference.wolfram.com/language/ref/CircularArcThrough.html.

CMS

Wolfram Language. 2022. "CircularArcThrough." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CircularArcThrough.html.

APA

Wolfram Language. (2022). CircularArcThrough. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CircularArcThrough.html

BibTeX

@misc{reference.wolfram_2023_circulararcthrough, author="Wolfram Research", title="{CircularArcThrough}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/CircularArcThrough.html}", note=[Accessed: 18-April-2024 ]}

BibLaTeX

@online{reference.wolfram_2023_circulararcthrough, organization={Wolfram Research}, title={CircularArcThrough}, year={2022}, url={https://reference.wolfram.com/language/ref/CircularArcThrough.html}, note=[Accessed: 18-April-2024 ]}